Keywords

Agricultural Production, Industrial Production, Economic Growth.

Introduction

Studies on the analysis of the phenomenon of economic growth have seen many scientific contributions and the formulation of mathematical models in recent years, and according to the different ideas of schools of economic thought with their contributions to the relationship of agricultural production and industry to economic growth, including the contributions of Nicholas Kaldor, and considering that agriculture and industry are among the main factors for development and growth, on top of that, as it receives increasing attention from most of the countries of the world, including Algeria, and this is what all the development programs of the five-year plans have witnessed. Although the contributions of the industrial and agricultural sectors to growth are low, the State seeks to develop these two sectors and increase their contribution to GDP.

Research Hypotheses

To answer the problem, we propose a set of hypotheses

1. There is a long-term equilibrium relationship between agricultural production and industrial production toward economic growth.

2. There is a significant positive relationship between agricultural production and industrial production toward economic growth in the short and long term.

3. There is a causal relationship between agricultural and industrial production toward economic growth.

Research Objectives and Importance

The study of the relationship between agricultural production and industrial production with economic growth is one of the important studies for the following considerations:

1. Estimate and test the relationship between economic growth, industrial growth, and agricultural growth in Algeria for the period 2000-2019 using an autoregressive joint integration model of distributed time intervals;

2. Know the impact of the growth of agricultural and industrial production on economic growth;

3. Testing the causal relationship between agricultural and industrial production and economic growth

The study is of scientific importance because the expected results help inform economic policymakers and decision-makers to develop plans and programs for the development of the industrial and agricultural sectors and thus contribute to agricultural, industrial, and economic growth in Algeria.

Research Methodology

The descriptive approach was adopted in order to fit the theoretical framework of the study by presenting and analyzing previous studies and providing basic concepts about the study. The quantitative approach was also used to measure the relationship between agricultural production and industrial production toward economic growth in Algeria.

Previous Studies and their Discussion

A study entitled: Achieving the impact of agriculture and industry on economic growth in India (Sahoo & Sethi, 2012); the study attempts to investigate the relationship between economic activity and the production of each of the agricultural and industrial sectors by using a standard methodology of the regression method (OLS). The findings show that industry and agriculture significantly contribute to India's economic development and prosperity. Based on the concurrent growth of both sectors, the analysis suggested the necessity of the both sectors’ development.

A study titled: The relationship between the agricultural and industrial sectors in Chinese economic development (Koo & Lou, 1997); a study looked at the interdependence between China's agriculture and industrial sectors. Traditional inputs, such as labor, are still crucial to Chinese economic development. The industrial sector of China grew greatly as a result of capital investment, while the agricultural sector did not. The findings also imply that China's economic growth has been significantly influenced by international commerce.

A study titled: The causality between agriculture, industry, and economic growth: Evidence from Indonesia (Bashir et al., 2019); this study looked at the interdependence between China's agriculture and industrial sectors. Traditional inputs, such as labor, are still crucial to Chinese economic development. The industrial sector of China grew greatly as a result of capital investment, while the agricultural sector did not. The findings also imply that China's economic growth has been significantly influenced by international commerce.

A study titled: The relationship between economic growth and agricultural growth: The case of China (Xuezhen et al., 2010); this article examines how agriculture contributes to economic growth by using econometric model analysis to examine China for the years 1952 to 2007. It shows that there has always been a positive relationship between agricultural and economic growth. In order for the national economy to grow quickly and in an orderly manner, it is necessary to continue enhancing agricultural contributions.

The Advantages of the Current Study over Previous Studies and their Discussion

Previous studies agreed on a common objective, which is to study the relationship between agricultural and industrial production and economic growth, and differed in the case study for the countries represented in Indonesia, India and China, as well as in the model used, which included the method of least squares, joint integration according to the autoregressive methodology for distributed time intervals for joint integration. Causality testing and results also varied. What sets this study apart is its use of the regression model, error correction model, and Granger causality to estimate and test the relationship between study variables (Al-Quraishi, 2007).

Results

Data Characterization

To study the relationship between agricultural and industrial production and economic growth, a case study on Algeria, annual time series were collected covering the period 2000 to 2019, and the variables following were used:

1. GDP growth (in annual %) and our symbol is GDP_ALG;

2. Value added in the agricultural sector (% of GDP) and our symbol is AGR_ALG;

3. Industry, value added (% of GDP) and our symbol is IND_ALG.

These data for these variables were collected from World Bank data, so the following Table 1 shows the description of the study data.

Table 1 Characterization of Study Data
Views	Standard deviation	Lowest value	Highest value	Average
2 0	1.629530	0.800000	7.200000	3.280000	GDP_ALG
20	1.711117	6.586678	12.38037	9.530814	AGR_ALG
2 0	7.888915	34.70136	58.88448	47.77659	IND_ALG

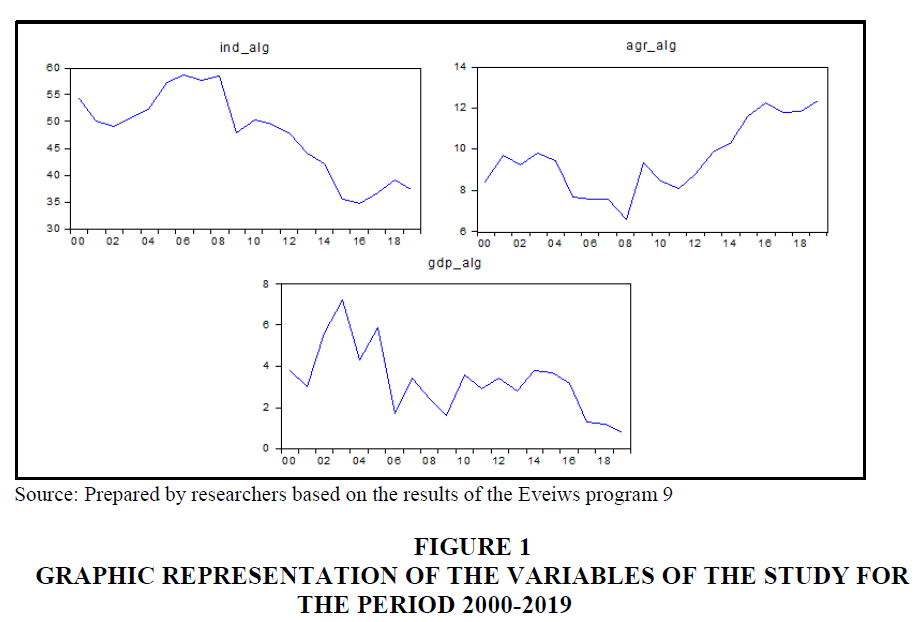
Here is a graphical representation of the time series of study variables Figure 1:

The study assumes that economic growth is affected by industrial and agricultural production, and to measure this effect, we will assume that the function takes the following form:

GDP_ ALG = f (AGR_ ALG, IND_ ALG)

The stability of the time series used in the study will be studied, then the co-integration test will be carried out, and the model will be estimated in the long and short term. The Granger causality test between the study variables will be carried out; we will rely on the morality levels 10%, 5%, and 1%, whether statistical morality or various tests, and we will use the econometric program eviews 9.

Time Series Stability Test

The unit root test is used to identify the degree of integration of the time series of study variables to see whether the variables are stable or not, so this test is considered the first step to ensure that the study variables are not quadratically integrated I(2) One or more to fulfill the condition for using the ARDL approach, and also to avoid false regressions, d especially since the macroeconomic variables are characterized by instability, according to a study by (Nelson & Plosser, 1982) and therefore, we will rely on the extended test of Dickey-Fuller and on the test of the null hypothesis according to which the existence of a unit root (that is, a time series of instability), and the following Table 2 shows the results of the unit root test.

Table 2 Results of the Unit Root Test (ADF)
The first difference			The level			Time series
Without constant or direction	Constant et direction	Only constant	Without constant or direction	Constant et direction	Only constant
***0.0077	***0.0002	***0.0000	0.3278	0.0358**	0.6938	GDP_ALG
***0.0000	***0.0023	***0.0009	0.8666	0.7541	0.7919	AGR_ALG
***0.0004	**0.0227	***0.0060	0.2111	0.7271	0.8208	IND_ALG

We note in the table above the results of the ADF test that all the variables have not stabilized at the I(0) level (with a constant or a trend with a constant or without a constant and a general trend), except for GDP_ALG it stabilized in the case of a trend with a constant alone, except that in first difference I(1) All the variables are stabilized (with a constant or a trend with a constant or without a constant and a general trend), and in Consequently, we conclude that each of the variables IND_ALG AGR_ALG, GDP_ALG, is stable in first difference I(1), and therefore the results of the tests allow the possibility of applying the ARDL model Figure 2.

Co-Integration Test using ARDL

Determining the appropriate slowdown period

From the figure, it is clear that the best model according to the AIC standard is ARDL (2, 4, 3) respectively are: (PIB_ALG, AGR_ALG, IND_ALG).

Boundary Approach Testing

Boundary testing depends on PSS F-TEST analysis, where the F-statistic value is calculated to test the joint significance of the parameters of the long-term variables, and then compared to the values reviews. If the calculated F-value exceeds the tabular critical values: the null hypothesis which indicates that there is no long-term relationship between the model variables and the alternative hypothesis which means the existence of a relationship in the longterm. The long-term relationship between the model variables is rejected, and the alternative hypothesis which means that there is a long-term relationship between the model variables, while if the calculated value of F is lower than the tabular critical values, then the null hypothesis is accepted. If the calculated F-statistic value falls between the lower bound and the upper bound of the tabulated F-value, the results will be indeterminate, which means the inability to make a decision to determine whether or not there is a co-integrating relationship between le variables (Shahbaz et al., 2008), and here are the results of the border curriculum test Table 3:

Table 3 Boundaries Studies Program Test Results
Test Statistic	Value	k
F-statistic	7.881180 ****	2
critical value limits
Indication level	lower bounds	Upper bounds
10%	2.63	3.35
5%	3.1	3.87
2.5%	3.55	4.38
1%	4.13	5

The table above shows the co-integration test using the linkage test methodology, such that the results indicate that the calculated F-statistic is greater than the upper limit at the 10%, 5%, 2.5, and 1%.%significance levels.

Therefore, we reject the null hypothesis which states that there is no co-integrating relationship between the variables, and we accept the alternative hypothesis that there is a long-term equilibrium relationship between the dependent variable and independent variables.

Results of the Error Correction Model to Measure the Short-Term Relationship

The Table 4 below shows that changing AGR_ALG & IND_ALG exerts a significant positive effect on GDP_ALG, at a 5% significance level and with slowed periods (1, 2, 3), indicating that there is a direct relationship between agriculture and industry. Agricultural production towards economic growth, and that this effect does not occur in the first year, but in the following periods, so that the increase in agricultural production (AGR_ALG) by one unit leads to an increase in the value of economic growth (GDP_ALG) by about 2 units, and the value of this effect decreases in future periods. High consumption and increasing industrial production (IND_ALG) by one unit cause the value of economic growth (GDP_ALG) to increase by about 0.35 units, and the impact value will increase in future periods. The industrial sector is increasing in the coming years.

Table 4 Results of the Error Correction Model
ARDL Co-integrating and long run form dependent variable: GDP_ALG
Variable	Coefficient	Std. Error	t-Statistic	Prob.
D(GDP_ALG(-1))	-0.458001	0.080422	-5.694971	0.0047
D(AGR_ALG)	-0.951138	0.424588	-2.240142	0.0886
D(AGR_ALG(-1))	2.467826	0.426369	5.78801	0.0044
D(AGR_ALG(-2))	2.177207	0.359375	6.058322	0.0037
D(AGR_ALG(-3))	0.49582	0.168572	2.9413	0.0423
D(IND_ALG)	-0.227103	0.11176	-2.032067	0.1119
D(IND_ALG(-1))	0.359071	0.103093	3.482993	0.0253
D(IND_ALG(-2))	0.478599	0.09626	4.971914	0.0076
CointEq(-1)	-0.393509	0.05298	-7.427534	0.0018
Co-integ = GDP_ALG-(-3.5289* AGR_ALG-0.3988* IND_ALG+53.7391)

It can be seen from the value of the error correction limit for a previous period, ECT-1, that it was statistically acceptable, indicating the existence of a long-term causal relationship between the independent variables and the variable dependent. Regarding the limit error correction coefficient, its value was (-0.3935) and its expected sign was negative and statistically acceptable, which confirms the existence of a long-term relationship between the variables. It clearly emerges that 39.35% of the imbalance of the previous period is corrected in the following period after any shock on the independent variables and affecting the dependent variable.

Long-term Relationship

It appears from the results of the table of long-term coefficients within the framework of the ARDL methodology for all the variables represented in agricultural and industrial production, which are not significant so that the model was not suitable for an estimation of the term to measure the impact, since the previous results suggest the existence of a relationship as well as expectations and economic theory Table 5.

Table 5 Results of a Long-Term Model
Long Run Coefficients
Variable	Coefficient	Std. Error	t-Statistic	Prob.
AGR ALG	-3.528941	2.799173	-1.260709	0.2759
IND ALG	-0.398838	0.536901	-0.742851	0.4988
C	53.739142	51.01859	1.053325	0.3516

Diagnostic Tests

Through the results of the serial correlation of the LM residuals (Appendix 01) that the Fisher probability is equal to 0.4842, which is greater than the level of significance of 5%, which makes us accept the null hypothesis that there is no serial correlation problem for the residuals of the regression equation, and through the results of the heteroscedasticity test of Breusch -Pagan-Godfrey (Appendix 02) We note that the Fisher probability is equal to 0, 6414 which is greater than the 5% significance level, which makes us accept the null hypothesis that there is no variance instability problem As for the normal distribution test (Appendix 03) for errors, the Jarque-Bera probability is 0.6667, which is greater than the 5% significance level, which supports acceptance of the null hypothesis that the residuals are normally distributed. Additionally, the results of the Ramsey test RESET TEST (Appendix 04) to test the validity and relevance of the determination n of the model, we note that the probability of the statistic F is equal to 0.7603, which is greater than 0.05 This proves the validity and relevance of the functional form used in the estimation.

Structural Stability Test for ECM-ARDL Parameters

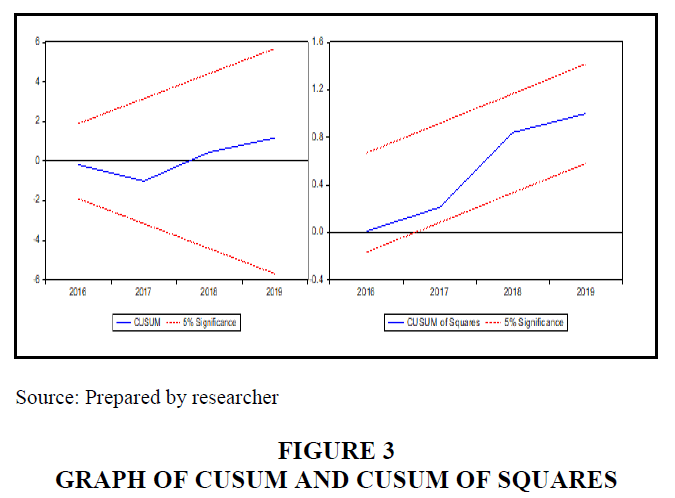
In order to ensure that the data used in this study are free from any structural changes, we use the appropriate tests: the cumulative sum of residuals (CUSUM) as well as the cumulative sum of squares of residuals (CUSUM of Squares).

The structural stability of the estimated coefficients of the error correction formula of the autoregressive model for the distributed temporal deviations is achieved if the graph of the CUSUM and CUSUM of squares tests fall within the critical limits at the 5% level of significance, and in the light of most of these studies we have applied these two tests proposed by Brown et al. (1975), so that the results of this test appear in the form of a curve of model errors estimated by the ordinary least squares (OLS) method, and a confidence interval to test the null hypothesis that the parameters of the OLS model are unstable. If the error curve is within the critical limits throughout the study period, then the null hypothesis is rejected at a significant percentage (5%), and this means that the parameters are stable throughout the study period. period of study, then the possibility of estimating fixed parameters of the model over the period of time of the study without the need to segment them into periods If the null hypothesis is rejected, the period of study must be divided into partial periods in which the parameters are stable Figure 3 (Brown et al., 1975).

It can be seen from these two tests, as shown above in the figure, that the sum of the residuals and the sum of the squares of the residuals are within a significant limit of 5%, which means that the model is structurally stable, which confirms the results of previous tests for the relevance of the model used and that its results are of high quality of reconciliation.

Granger Causality Test Results

To examine which variables in the study influence which others, we will first determine. The appropriate degree of delay and following are the results of the appropriate degrees of delay according to a set of criteria for degrees of a delay from 0 to 2 Table 6:

Table 6 Results of Appropriate Degrees of Delay
Lag	LogL	LR	FPE	AIC	SC	HQ
0	-110.7998	NA	62.24838	12.64442	12.79282	12.66488
1	-84.83346	40.39205*	9.662616*	10.75927*	11.35285	10.84112
2	-77.51714	8.942174	12.96594	10.94635	11.98512	11.08958
* indicates lag order selected by the criterion
LR: sequential modified LR test statistic (each test at 5% level)
FPE Final prediction error
AIC: Akaike information criterion
SC: Schwarz information criterion
HQ: Hannan-Quinn information criterion

The appropriate degree of lag for the lowest values of all criteria in the range 0-2 is 1, and the result of the Granger causality test between the variables (GDP_ALG, AGR_ALG, IND_ALG) with a degree of lag was the next Table 7:

Table 7 Results of the Granger Causality Test
Lags: 1
Null Hypothesis	Obs	F-Statistic	Prob.
GDP_ALG does not Granger Cause AGR_ALG	19	0.46861	0.5034
AGR_ALG does not Granger Cause GDP_ALG		0.05377	0.8196
IND_ALG does not Granger Cause AGR_ALG	19	6.58835	0.0207
AGR_ALG does not Granger Cause IND_ALG		6.48302	0.0216
IND_ALG does not Granger Cause GDP_ALG	19	0.23056	0.6376
GDP_ALG does not Granger Cause IND_ALG		1.2515	0.2798

Above table presents the results of causality between the variables under study The results of the estimation of the short-term causality relationship between all the variables of the study indicate the existence of a relationship of causality between industrial production and agricultural production, since the F-statistic reaches (6.588) with a probability of (0.207), so we accept the hypothesis that a change in industrial production leads, according to Granger's concept, changes in the value of agricultural production, and there is also an inverse causal relationship between the above, according to the F statistic, with a value of (6.48) with a probability of 0.0216. As for testing the hypothesis of a causal relationship running from the value of industrial production, from production to agricultural growth to economic growth, the results indicate that there is no causal relationship.

Through this study which examines the relationship of agricultural production and industrial production with economic growth using the ARDL model, the case study of Algeria for the period 2000-2019 shows the following:

1. Each of the time series (for the variables IND_ALG & AGR_ALG & GDP_ALG) used in the study is stable to the first difference I(1).

2. Using co-integration using boundary test methodology, it was found that there is a long-term relationship between the variables.

3. There is a direct and moral short-term relationship between the two variables of IND_ALG & AGR_ALG towards economic growth.

The agricultural sector has a greater impact than the industrial sector on economic growth, but the impact of the agricultural sector decreases in the coming years, while the impact of the industrial sector increases in the coming years.

1. The estimated error-correction model showed the ability to return to the point of equilibrium and long-term adjustment; the model also realizes the structural stability of the estimated coefficients of the error-correction formula for the autoregressive model for the distributed time intervals.

2. The existence of a reciprocal causal relationship between industrial production and agricultural production according to Granger's concept.

References

Al-Quraishi, M. (2007). Economic development-theories, policies and topics. Dar Wael, Amman, 69.

Google Scholar

Bashir, A., Suhel, A., Azwardi, A., Atiyatna, D.P., Hamidi, I., & Adnan, N. (2019). The causality between agriculture, industry, and economic growth: Evidence from Indonesia. Etikonomi, 18(2), 155-168.

Indexed at, Google Scholar, Cross Ref

Brown, R.L., Durbin, J., & Evans, J.M. (1975). Techniques for testing the constancy of regression relationships over time. Journal of the Royal Statistical Society, 37(2), 149-163.

Indexed at, Google Scholar, Cross Ref

Koo, W.W., & Lou, J. (1997). The relationship between the agricultural and industrial sectors in Chinese economic development.

Indexed at, Google Scholar

Nelson, C.R., & Plosser, C.R. (1982). Trends and random walks in macroeconmic time series: Some evidence and implications. Journal of Monetary Economics, 10(2), 139-162.

Indexed at, Google Scholar, Cross Ref

Sahoo, K., & Sethi, N. (2012). Investigating the impact of agriculture and industrial sector on economic growth of India. OIDA International Journal of Sustainable Development, 5(5), 11-21.

Indexed at, Google Scholar

Shahbaz, M., Ahmad, K., & Chaudhary, A.R. (2008). Economic growth and its determinants in Pakistan. The Pakistan Development Review, 471-486.

Indexed at, Google Scholar, Cross Ref

Xuezhen, W., Shilei, W., & Feng, G. (2010). The relationship between economic growth and agricultural growth: The case of China. In 2010 International Conference on E-Business and E-Government, 5315-5318.

Indexed at, Google Scholar, Cross Ref

Received: 12-Dec-2022, Manuscript No. BSJ-22-12996; Editor assigned: 14-Dec-2022, PreQC No. BSJ-22-12996(PQ); Reviewed: 28-Dec-2022, QC No. BSJ-22-12996; Revised: 11-Jan-2023, Manuscript No. BSJ-22-12996(R); Published: 18-Jan-2023