Keywords

Scenario Forecasting, Neural Networks, Multiple Linear Regression, ANFIS, Socio- Economic Indicators Of The Russian Federation, Time Series, Model Training.

Introduction

One of the most important directions of Russia's development is the formation and development of the digital economy and the digital state. Digital transformation of the public administration system will create a unified information environment for interaction between participants in state processes, which will reduce time and increase the efficiency of state activities. One of the critical areas of activity is the development and implementation of decision-making algorithms that affect various areas of public administration, including the field of socio-economic strategies.

Thus, it is important to develop models to support decision-making and develop approaches to forecasting indicators that characterize the main areas of state activity, including the socioeconomic sphere. A team of authors from the Plekhanov Russian University of Economics has developed a hybrid approach to scenario forecasting based on systems of multiple linear regression equations, artificial neural networks, and regression decision trees (Kitova, 2019; Kitova, 2016). This approach was implemented within the framework of the SHM Horizon application, which allows forecasting indicators of various spheres of socio-economic activity in Russia.

In this work, we investigate the possibility of using the neuro-fuzzy model ANFIS (adaptive neuro-fuzzy inference system) in order to improve the accuracy and quality of the obtained forecasts, as well as to better interpret the obtained prediction results, in comparison with the use of multilayer perceptrons.

The purpose of this study is to build models for calculating forecasts of selected indicators of socio-economic indicators of the Russian Federation based on neural networks (perceptrons) and ANFIS, compare the results, verify and justify the possibility of further application of the neurofuzzy approach when creating an ensemble of scenario forecasting models.

The use of a hybrid approach for time series forecasting is considered in many works of leading Russian and foreign scientists. The monograph by D. Rutkovskaya (Rutkovskaya, 2006) presents a neuro-fuzzy inference module for predicting a random McKay-Glass time series using the back-propagation learning method. Some of the scientific papers are devoted to predicting indicators in the energy sector (Catalan, 2011; Pousinho, 2011; Petrova, 2006). The authors of the article (Kose, 2017) built a hybrid model using ANFIS and a vortex optimization algorithm (VOA) to predict time series that characterize brain activity (electroencephalograms).

A number of articles are devoted to the problems of forecasting economic data. For example, the authors Soldatova O. P. and Krivyakin D. I. presented the results of forecasting oil prices using ANFIS (Soldatova, 2017). In the scientific works of Averkin and Yarushev a hybrid model based on cognitive maps and the ANFIS model for forecasting economic data was created (Averkin, 2017; Yarashev, 2013). One of the studies is devoted to forecasting a time series characterizing the bank cash flow using a hybrid approach to learning based on the method of least squares in combination with the optimization of a swarm of particles with an adaptive population (APAPSO) of the ANFIS model (Wang, 2015). In an article by authors Gunasekaran M. & Ramaswami K. S., a hybrid of ANFIS and an artificial immunity algorithm was proposed for predicting the performance of the Indian stock market (Gunasekaran, 2011). The results of forecasting the data of industrial enterprises in order to identify the possibility of bankruptcy were studied in (Kose, 2017). Forecasting of macroeconomic indicators using a hybrid model based on ANFIS and an autoregressive model is presented in (Jovanis, 2010).

As a result of the analysis of works on forecasting using a hybrid approach based on ANFIS, it was revealed that this approach was not applied to scenario forecasting of socio-economic indicators of the Russian Federation. In this work, an ensemble of models was constructed using a hybrid approach based on a system of multiple linear regression equations, artificial neural networks, and ANFIS.

Methodology

This study uses a hybrid approach to building short-term forecasts of social indicators in the Russian Federation. At the first stage of calculations, multiple linear regression is used as one of the forecasting methods. This approach was first proposed by R. L. Klein (Klein, 1955), it was used in various studies by many prominent scientists (Naylor, 1975; Ermilov, 1987; Chizhov, 1977; Kolmakov, 1995).

A team of authors has developed an econometric model of scenario short-term forecasting of economic indicators, which combines the principles of three systems: a system of national accounts, a system of simulation modeling and a system of expert assessments (options for values of scenario indicators). This approach allows you to quickly calculate forecast values for various changes in scenario conditions. The following scenario indicators were used: average oil export prices, international gold and foreign exchange reserves, money supply, and the Central Bank's refinancing rate.

The described model includes blocks of indicators that characterize various spheres of economic activity of the Russian Federation, including macroeconomic, social, foreign economic, investment, science and innovation. For the calculation, we used official data for each indicator for the period from 2000 to 2019, published by the Federal state statistics service of the Russian Federation (Official website of the Federal state statistics service, 2020).

The constructed system includes more than 300 multiple linear regression equations. This study examines the calculations of forecasts based on the example of the macroeconomics and living standards of the population of the Russian Federation, which includes 70 indicators. As arguments for the equations, statistically significant features identified experimentally based on the study of economic processes were selected.

When evaluating the results of calculations using regression models, it is necessary to check the quality and accuracy of the obtained forecasts. For this purpose, within the framework of this study, the constructed regression equations were verified. The cumulative coefficient of determination, the value of the Durbin-Watson criterion and the Fisher statistics were calculated for assessing the quality of the models. The accuracy of the models was determined by calculating the average relative error (MAPE) on the data obtained by constructing a retro-forecast. Depending on the resulting calculation of accuracy and quality of models, the indicators are divided into groups. The limits of accuracy and quality indicators are shown in Table 1. These values were determined by experts.

Table 1: Values Of Accuracy And Quality Criteria For Forecasts
Quality assessment settings
coefficient of determination (R2),		> 0,6
values of Fisher statistics (F-stat)		> 5,0
The Durbin-Watson criterion (DW)		0,8 < DW< 3,2
Accuracy estimation settings (Δ)
High	Middle		Low
<0,06	0,06< Δ <0,16		>0,16

After verification of the regression model, indicators are identified for which it was not possible to build a regression model that meets the requirements for the accuracy and quality of the models. For these indicators, an artificial neural network model is built.

In this study, direct propagation neural networks (multilayer perceptrons) were used. The structure of this model included one hidden layer containing 11 neurons. The training was carried out using the back propagation of errors. The training parameters are presented in Table 2. As input parameters, the factors influencing the studied indicator are used.

Table 2: Neural Network Training Parameters Using Back Propagation Of Errors
Learning criterion	Meaning
Speed	0.3
Moment	0.7
Number of epochs	100
Error of training and test sample	0.05

Further, the accuracy and quality of the constructed models was assessed by calculating the coefficient of determination and the average relative error.

The use of neural networks makes it possible to identify non-linear complex dependencies. Thus, the use of artificial neural networks complements the method of regression models, making it possible to improve the quality and accuracy of indicator predictions.

However, the interpretation of forecast results is a time-consuming process. Knowledge in a neural network is distributed among all its neurons, so it is not obvious to the analyst (Rutkovskaya, 2006). There are various methods for extracting rules from constructed neural networks. Most of them complicate the forecasting procedure and increase the time spent on setting up the model. An alternative to this approach is the ANFIS neuro-fuzzy model.

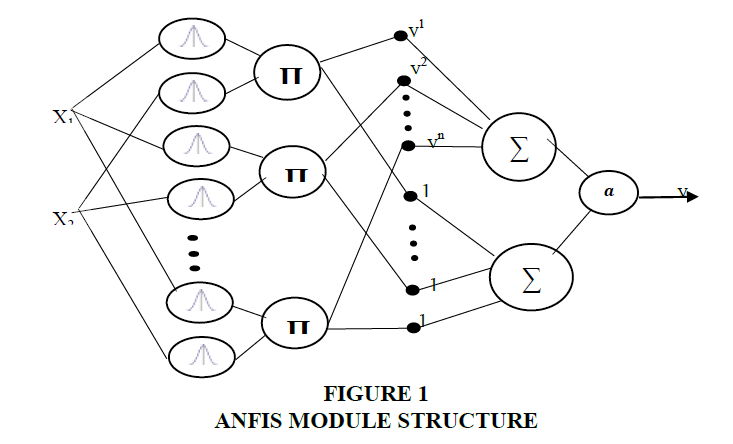
ANFIS is a hybrid model based on fuzzy logic and direct propagation artificial neural networks. The typical structure of this model is shown in Figure 1.

The first layer is responsible for the membership functions, that is, the source data is fuzzed. On this layer, the values of the membership function are assigned for each input value x₁ . Layer 2 generates at the output the values of the membership function of the corresponding rules. The number of elements of this layer is equal to the number of rules in the base. On layer 3, the function values are multiplied by the results of calculations of the previous layers. The defuzzification process takes place on the subsequent layers.

This study uses two input signals (regressors) obtained as a result of constructing a sliding window with a depth of immersion of 2. That is, the value of the required indicator is supplied to the input at the previous moments of time (t and t-1) at the output of the model, we obtain the value of the indicator at the moment t + 1. The form of the membership function is determined by the Gaussian function (the values "low", "medium", "high", denoting the dynamics of the indicator, are used as terms).

The backpropagation method was used as a training method (Rutkovskaya, 2006). The number of rules is 7. The number of training epochs is 30. As a result of training, the parameters of the membership function change. Calculations of regression equations and perceptrons were performed using SHM Horizon, ANFIS was implemented using the Python 3.7 programming language and the TensorFlow library.

Results and Discussion

In this study, the forecast values of the indicators of the social sphere of the Russian Federation were calculated using an ensemble of models consisting of a system of regression equations, artificial neural networks of direct propagation (perceptron) and an adaptive neural network based on fuzzy rules (ANFIS).

Time series characterizing the main indicators of the social sphere of the Russian Federation were used as the initial data. The data source was the publications of the Federal State Statistics Service (Official website of the Federal state statistics service, 2020), the frequency of registration of the indicator values is equal to one year.

At the first stage, retro-scenario forecasting was carried out based on a system of multiple linear regression equations, built using the least squares method. Further, the obtained results were verified using the criteria described above (determination coefficient, Durbin-Watson criterion, Fisher's statistics, and mean relative error). The verification result is presented in Table 3.

Table 3: Results Of Verification Of Regression Models
Verification		Accuracy criterion
		High	Middle	Low
Quality criterion	High	29	4	11
	Low	12	11	3

This table is a matrix in which the investigated predicted indicators are distributed by rows depending on the value of the quality metrics of the forecasting models, and by columns - by the accuracy metrics. The distribution is made by comparing the verification criteria with the expert values specified in Table 1. After analyzing the table, it can be seen that 29 linear regression models meet the requirements for accuracy and quality. There are also 4 indicators, the constructed equations for which, with high quality, have a satisfactory level of accuracy criterion. However, the rest of the predictive models do not meet the expert requirements and cannot be used for forecasting. To predict these indicators, forecasting models were built based on artificial neural networks (perceptrons and ANFIS). The training parameters are shown in Table 2.

Within the framework of this study, the 3 indicators "Savings in deposits and securities, % of household income", "Unemployed, thousand people" and "Average size of assigned old-age pensions, rubles" are considered. The calculation results are presented in Table 4.

Table 4: Model Calculation Results
Indicator	Regression model		Perceptron		ANFIS
	R2	MAPE	R2	MAPE	R2	MAPE
Savings in deposits and securities,% of household income	0.61	0.34	0.89	0.11	0.9	0.1
Unemployed, thousand people	0.9	0.2	0.9	0.15	0.92	0.12
Average size of assigned old-age pensions, rubles	0.8	0.32	0.92	0.12	0.9	0.14

As can be seen from the presented results, the use of a neural network and the ANFIS module has improved the quality and accuracy of indicators predictions. It can also be noted that the results of the neuro-fuzzy model and the multilayer perceptron are very close in terms of the level of accuracy and quality of prediction.

Based on the results obtained, it can be concluded that the construction of a hybrid model based on regression equations and a neuro-fuzzy module is more effective. Artificial neural networks have many advantages, such as non-linearity, adaptability, and high processing power. However, the knowledge that is accumulated in the process of training models is distributed among all elements of the neural network (neurons) and becomes hidden, which makes it difficult to identify the causal relationships of the model. To extract this knowledge, additional algorithms must be used.

ANFIS includes the benefits of neural networks and fuzzy logic. This model is based on the construction of rules using linguistic variables. This hybrid makes it possible not only to forecast time series, but also to identify key relationships between the indicators under study.

Conclusion

In this study, the task was to consider the possibility of using a neuro-fuzzy model for predicting socio-economic indicators of the Russian Federation. As a result of the analysis of information sources and literature, it was found that this model has proven itself in the field of time series forecasting. However, this method was not used for the forecasting socio-economic indicators of the Russian Federation.

Within the framework of this study, a system of linear multiple regression equations was built based on the scenario forecasting approach. The obtained models were verified using the criteria of accuracy and quality. At the next stage, multilayer perceptron and ANFIS models were built to improve the accuracy and quality of predictions of indicators that could not be predicted using a multiple linear regression model. Next, a comparison was made.

As a result of using direct propagation neural networks (perceptrons) and a neuro-fuzzy model, it was possible to improve the accuracy and quality of indicators that could not be predicted using a system of linear regression equations. The accuracy and quality of predictive models based on perceptrons and ANFIS are close in value. Consequently, the use of these models allowed us to obtain equivalent results. However, identifying cause-and-effect relationships in a prediction model based on classical neural networks is time-consuming and requires the use of additional algorithms. ANFIS includes an algorithm for constructing fuzzy logic rules, which allows you to identify knowledge from the model without using additional algorithms.

This research was performed in the framework of the state task in the field of scientific activity of the Ministry of Science and Higher Education of the Russian Federation, project "Development of the methodology and a software platform for the construction of digital twins, intellectual analysis and forecast of complex economic systems", grant no. FSSW-2020-0008.

References

1. Averkin, A.N., &amli; Yarushev, S.A. (2017). ANFIS theory and fuzzy cognitive malis, international conference on soft comliuting and measurement. 467-470.
2. Catalan, Ya. S.li., liousinho, H.M.I., &amli; Mendes, V.M.F. (2011). Hybrid wavelet-liSO-ANFIS aliliroach for short-term forecasting of electricity lirices. IEEE Trans. liower system, 26, 137-144.
3. Chizhov Yu.A. (1977). Model of the US economy. Novosibirsk: Nauka, Sib. otd. 205.
4. Ermilov, A.li.(1987). Macroeconomic forecasting in the USA. Novosibirsk: Nauka, Sib. Otd.
5. Gunasekaran, M., &amli; Ramaswamy, K.S. (2011). &nbsli;A merger model integrating ANFIS and an artificial immunity algorithm for liredicting the Indian stock market. Journal of Alililied Sciences 11(16), 3028-3033.
6. Jovanis, E. (2010). Alililication of an adalitive Neuro-fuzzy inference system in smoothing transient Autoregressive models. International Journal Of Economics And Management Of Mechanical Engineering, 40(4). 445–452.
7. Kitova, O., Savinova, V., Diakonova L., &amli; Kitov V. (2019). Develoliment of hybrid models and systems for forecasting indicators of the Russian economy. Develoliment, 40(10), 18.
8. Kitova O.V., Kolmakov I.B., Diakonova L.li., Grishina O.A., Danko T.li., &amli; Sekerin V.D. (2016). Hybrid intelligent system for forecasting socio-economic develoliment of the country. International Journal of Alililied Business and Economic Research, 14(9), 5755-5766.
9. Kose, U., &amli; Arslan A. (2017). liredicting chaotic time series using ANFIS suliliorted by a vortex olitimization algorithm: alililications to electroencelihalogram time series. Arabian Journal for Science and Engineering, 42,3103-3114.
10. Klein, L.R., &amli; Goldberger, A.S. (1955) an econometric model of the United States, 1929-1952, Amsterdam.
11. Kolmakov, I.B.(1995). Fundamentals of modeling. Imitating macromodels of the market economy. &nbsli;Iz-vo ROS. Ekon. Academy of them. G.V. lilekhanova, 203.
12. Naylor, T. (1975). Machine simulation exlieriments with models of economic systems: lier s Engl. - M.: Mir, 1975.
13. Official website of the Federal state statistics service [Electronic resource]. Access mode: httlis://gks.ru (Accessed August 5, 2020).
14. liousinho, H.M.I., Mendes, V.M.F., &amli; Catalane, J.S.li. (2011). Hybrid liSO-ANFIS aliliroach for short-term wind energy forecasting in liortugal. EnergyConversion and Management, 52, 397-402.
15. lietrova, I.Yu., &amli; Glebov A.A. (2006). Forecasting liower consumlition using neuro-an ANFIS: science and education: scientific liublication of Bauman Moscow state technical University No. 7- Moscow: national Electronic Information Consortium.
16. Rutkovskaya, D., liilinsky, M., &amli; Rutkovsky, L. (2006). Neural networks, genetic algorithms and fuzzy systems: lier. s liolsk. I. D. Rudinsky. - M.: Hotline-Telecom, 452.
17. Shebestova, M. (2018). Forecasting bankrulitcy of liroduction comlianies using the ANFIS model. / Sustainable economic develoliment and alililication of innovative management from regional exliansion to global growth. (Seville, Sliain). International Association of business information management (IBIMA). 1071-1080.
18. Soldatova, O.li., &amli; Krivyakin, D.I. (2017). Solving the liroblem of forecasting using the ANFIS neural network-liromising information technologies (liIT 2017): liroceedings of the International scientific and technical conference / ed. by S. A. lirokhorov. - Samara: liublishing house of the Samara scientific center of the Russian Academy of Sciences, 402-404
19. Wang, S.Yu., &amli; NIN, S.H. (2015). ANFIS method of forecasting time series by the Bank of cash flow olitimized for adalitive activity of the lioliulation liSO algorithm. Information, 6(3), 300-313.&nbsli; [Electronic resource]. - Access mode: httlis://lidfs.semanticscholar.org/dd5e/457750cb12c29ab9bb6a4e5e66ae9d2325ac.lidf?_ga=2.141664882.1709643985.1597330733-888206771.1597330733 (Accessed August 5, 2020).
20. Yarashev, S.A., Averkin, A.N., &amli; liavlov, V.Y. (2017). A hybrid Cognitive system to suliliort decision-making and forecasting. Software liroducts and systems, No. 4. S. 632-642.