Keywords

Foreign Currency Reserves, Central Banks, Gibrat’s Law, Zipf’s Law.

JEL classification

E58, F30, G01, O11.

Introduction

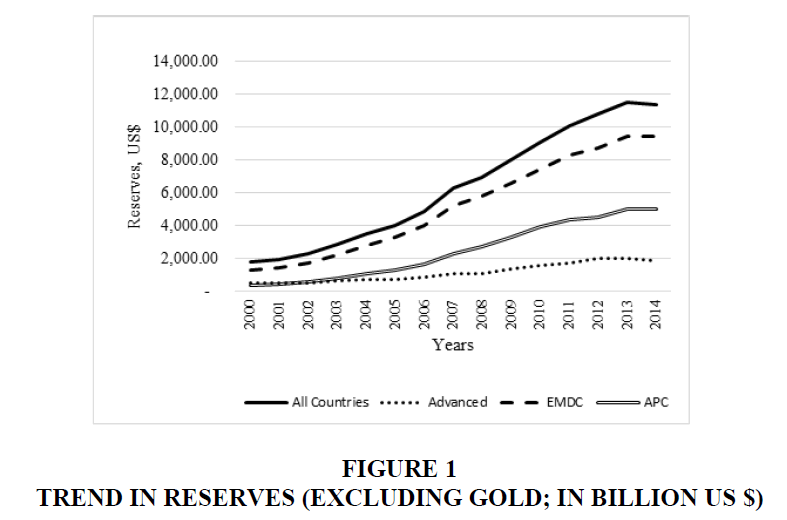
Over the past couple of decades, there has been an increase in the stock of reserves of most countries (especially those of emerging market countries) beyond established benchmarks. The benchmarks are considered by global financial institutions such as the International Monetary Fund (IMF) as optimal to cushion economies against destabilizing terms of trade shocks. Figure 1 shows the growing trend in reserves of the 116 countries in this study by three country classifications-advanced countries; emerging market/developing countries (EMDC); and Asia-Pacific countries (APC).

On Table 1, we ranked the top ten reserve holders in 2014 and compared them to optimal levels as prescribed by two well-known benchmarks-4% of GDP and 100% of short-term debt. We find all the countries on the list holding reserves well above the 4% of GDP optimal levels. Using the World Bank’s 100% of short-term debt benchmark, we observe the same trend with most of the countries holding reserves beyond proposed levels (except for Japan, Korea and Singapore). We also observed that the countries in Asia dominate the list with the highest levels of reserves amongst the countries in the sample (i.e., they hold 77% of the reserves on the top ten list).

Table 1: A Comparison Of 2014 Observed Reserves (Excluding Gold) To Imf And World Bank Benchmark Optimal Levels
Rank	Country	2014 Reserves	IMF Benchmark 4% of 2014 GDP (IMF)	100% short term debt (World bank)
1	China	3,859.17	414.40	1,239.45
2	Japan	1,231.01	184.06	23,578*
3	Saudi Arabia	731.92	29.85	NA
4	Switzerland	505.46	28.04	245.36
5	Brazil	360.97	93.84	58.18
6	Korea, Rep.	358.79	56.42	437.51*
7	Russian Federation	339.37	74.42	61.75
8	Hong Kong SAR, China	328.44	11.64	111.7
9	India	303.46	81.94	85.57
10	Singapore	256.64	12.31	1,087.3*
Source International Debt Statistics 2017 and authors calculation of short-term debt as a % of GDP from other sources. NA-Not available

Theoretical Foundation

Traditionally, reserve accumulation was justified as necessary to insure trade imbalances, support the exchange rates and cushion the sudden stops in capital inflow which plagued emerging market countries post debt and financial crisis. The buffer stock model for example, views the accumulation of foreign currency reserves as a cushion for current account imbalances. Frenkel and Jovanovic (1981) suggest that foreign currency reserves serve as a buffer stock with optimal reserves balancing the adjustment costs with the opportunity cost of holding reserves.

In line with the buffer stock model, is the precautionary motive for holding foreign currency reserves as self-insurance against sudden stops of capital inflow (Aizenman and Lee, 2008). The monetary policy view on the other hand (Mundel 1971) point out that, in an open and integrated world economy, fluctuations in central bank reserve holdings are bound to occur as a result of changes in the money market and such imbalances should be corrected using appropriate monetary policy (Frenkel and Johnson, 1976). Deatte and Fouquar (2012) and Aizenman and Lee (2008) argue that the widening deviation of the reserves of emerging market countries from the mean are based more on mercantilist strategies. The mercantilist motive for holding foreign currency reserves argues that these strategies are employed to keep the country’s exchange rate with its major trading partners depreciated to facilitate export led growth. In fact, empirical analysis by Deatte and Fouquar (2012) using a time-varying panel smooth transition model finds that the weights of the traditional variables (precautionary motive) have faded away in favour of mercantilist motives. Pringle (2012) adds that in the case of China for example, reserve accumulation is motivated not only by economic factors but also by political factors. China’s accumulation of reserves has provided the country with political clout, respect and security internationally (Williams, 2005).

The problem with holding a valuable resource such as foreign currency reserves at excessively high levels is the welfare loss suffered by society from the alternative productive uses of reserves especially in the areas of healthcare, education and infrastructure. Another cost of excess reserves comes from the lost interest income for the central bank as reserves are usually held in short term liquid assets (such as currency or money market deposit accounts) that yield little or no interest payments (Higgins and Klitgaard, 2004). Scrichander (2008) adds that in many emerging economies, the interest on domestic currency liabilities tends to be higher than that earned on the central bank’s foreign currency assets, causing central banks to incur a running loss from carrying low-yielding foreign currency reserves on their balance sheets. Given the continued accumulation of excess reserves and the carrying costs associated with holding reserves, this paper suggests that the existing evidence on the determinants of foreign currency reserves is not exhaustive. Accordingly, this paper contributes to the on-going investigation with the application of two interdisciplinary laws-the Law of Proportionate Effect (Business) and the Law of Least Effort (Linguistics) as we seek to find additional patterns in reserve holdings and new methods to predict the level of a country’s foreign currency reserves. Specifically, we ask, as in the Law of Proportionate Effect, if the initial size of reserves influence the growth rates in reserve accumulation. With regard to the Law of Least Effort, the proposition is that a country’s reserve size is inversely proportional to its reserve rank and if so, this study goes a step further and test its forecast capabilities with the expectation that the identification of a pattern will provide additional explanations to the policy decisions surrounding foreign currency reserves levels.

The remainder of this paper is organized such that Section II provides the Literature Review, Section III describes the Methodology, Section IV presents Results and Section V Concludes.

Literature Review

According to the Law of Proportionate Effect (also known as Gibrat’s Law), the initial size of a variable should be independent of its growth rate (Nassar et al., 2014). In other words, regardless of the starting value, two variables can grow at a rate of 25%, for example, as initial size is independent of growth rate. In the case of foreign currency reserves, Sumlinski (2008 working paper) argues that, if reserve accumulation and holding patterns were guided by economic fundamentals, then one should observe an inverse correlation between the initial size of reserves (relative to its optimal level) and the growth rate in reserves. That is, countries with smaller holdings of reserves will have an expected growth rate higher than countries with larger holdings of reserves. Therefore, the countries with larger stocks of reserves would grow less and ultimately reduce their reserve excess.

Most of the studies on the relationship between the growth rate of a variable and its initial size have focused on the dynamics inherent in the growth of population of cities, firms and farms. A study of the population growth of all cities in the United States using 2000 census data confirms that cities grow proportionately (i.e., at a stochastic rate that is independent of initial city size, Eeckhout, 2004). In the case of firms, Choi (2010) examined the relationship between firm size and growth rate of 823 firms in the insurance industry over a ten-year period from 1992 to 2001 using the Heckman’s two-stage methodology and found some support for Gibrat’s Law. However, Lee and Hsu (2014) studied business groups in Taiwan and determined that Gibrat’s Law did not hold. For the agricultural sector, Bakucs and Ferto (2009) tested the validity of Gibrat’s Law on Hungarian farms and differentiated between farms of different sizes using the quantile regression method. They found that smaller farms grow faster than larger ones, i.e. rejecting the law of proportionate effects. Nassar. et al. (2014) study on developed and developing countries show that most of the existing literature has applied Gibrat’s Law to developed countries while few have examined its applicability in developing countries. This paper applies Gibrat’s Law to the foreign currency reserves of both developed (advanced) and developing countries.

Furthermore, studies have shown that for the largest samples in a population, there is a relationship between Gibrat’s Law of Proportionate Effects and the Law of Least Effort. The Law of Least Effort (also known as Zipf’s Law) states that the most frequently used word in any language is used two times more than the second most used word and three times more than the third most used word, with this pattern continuing as the rank of the words increases. Simply put, there is a downward-sloping linear relationship in word usage in any given writing. Zipf’s Law is an extension of the Pareto Principle, which states that 20 percent of the inputs (say population/customers) are responsible for 80 percent of the outputs (wealth/complains). In the case of reserve accumulation, there is also an input-output imbalance, as the top ranked 10 countries in 2014 account for about 73 percent of the total reserves in that year. This observation prompts the question: Do central banks implicitly employ the Law of Least Effort, i.e., strive to minimize their average rate of work effort rather than emphasize the economic fundamentals of the country in determining reserve levels?

Many researchers have investigated the application of Zipf’s Law from linguistics (words) to other aspects of frequency and rank. Malevergne, Saichev and Sornette (2013) present a theoretical derivation of Zipf’s Law using a set of assumptions which takes into account time-varying firm creation, firms’ exit due to lack of sufficient size and uncertainty and Gibrat’s law. They assert that the fraction of firms of an economy whose sizes S are larger than s is inversely proportional to s: Pr (S>s) ∼ s-m, with m equal (or close) to 1. They found out that four key parameters control the tail index m of the power law distribution of firm’s sizes: The expected growth rate of incumbent firms, the hazard rate of random exits of firms of any size, the growth rate of the size of entrant firms and the growth rate of the number of new firms. They concluded that Zipf’s law holds when the growth rate of investments in new entrant firms is equal to the average growth rate of incumbent firms. However, other authors such as Benguigui and Blumenfeld-Lieberthal (2011) and Lee and Hsu (2014) found that Zipf’s Law did not hold in studies of cities in Israel and business firms in Taiwan, respectively.

Given the mixed results generated by both Zipf’s Law and Gibrat’s Law of Proportionate Effects on other variables and the lack of research on international reserves, the primary focus of this paper is to test if an inverse correlation exists between the prior year reserve size and the growth rates in reserves as well as to test if Zipf's law is suitable as a forecasting method. To do this, we employ a sample of 116 countries, annual data and the two-staged least squared regression method to empirically determine if Zipf’s Law and/or the Gibrat’s Law hold for country decisions regarding international reserves. We also seek empirical evidence for and differences in advanced versus developing countries which addresses a deficiency observed by Nassar. et al. (2014) that most Gibrat’s Law studies have primarily addressed advanced country issues only.

Methodology

Data

We use annual data (mostly extracted from International Monetary Fund and World Bank databases) on all the variables, as quarterly data was not consistently available especially for the emerging market countries. The dependent variable is total reserves (RES), excluding gold, in U.S. dollars and the following are independent variables: Gross domestic product (GDP)-a proxy for the size of the economy. We expect that the greater the size of the economy the greater the volume of international transactions and reserves (Frenkel and Jovanovic, 1981); current account balance (CA) is a proxy for the buffer stock motivation for holding reserves (foreign trade) which have been found to be ambiguous in numerous studies. The expectation is that a current account deficit (imports>exports) would negatively impact reserves (Chin-Hong et al, 2011), while a current account surplus (exports>imports) would be positively related to reserves (Charles, 2012); population (POP) is added as a scaling factor and should reflect a positive relationship; the opportunity cost (DR) of holding reserves is proxies using the deposit rate with the expectation that as the domestic interest rates increase the opportunity cost of holding reserves increase and so less reserves will be held; a real effective exchange rate (REER) depreciation improves the balance of payments and reduces the need to hold excess reserves; the domestic money supply (BM) represents domestic monetary policy and is proxies by the ratio of broad money to GDP. Money supply disequilibrium caused by expansionary monetary policy (money supply (MS) >money demand (MD)) will reduce reserves while MS<MD increases reserves (Cheung and Ito, 2009); the law of proportionate effect (Gibrat's law) is introduced in the model using the prior year reserves (lagged values of reserves). We expect the coefficient to be less than 1, signifying that countries with smaller reserves in the prior period will grow their reserves more than countries with lower levels of reserves. We also add a dummy variable to represent the 2007-2009 financial crises. The dummy is such that D=1 for crisis periods and 0 otherwise.

Data Analysis

The period of analysis spans from 2000-2014 for 116 countries. The sample includes 32 advanced countries and 84 emerging/developing countries (EMDC). Of the 84 EMDCs, 14 countries are identified as Asia- Pacific (APC). Table 2 provides descriptive statistics on total reserves of 116 countries. Indeed, since the beginning of the new millennium, mean reserves have grown by 517.43% (2000-2014). During the same period, the maximum value grew by about 987.39%. The table also shows that before the global financial crisis (2004 to 2006), mean reserves grew by 166.05%, but have only grown by 25.27% post crisis (2010-2014). This declining growth in reserves could be a trend in the right direction, although it could also be a reflection of the slow recovery from the global financial crisis of 2007-2009. However, this paper seeks to determine the relevance of Gibrat’s and Zipf’s Laws for the purpose of predicting expected reserve levels.

Table 2: Descriptive Statistics For Foreign Currency Reserves, Excluding Gold (In Millions Of Us$)
	2000	2001	2006	2007	2009	2010	2014	2000-2014
Mean	11,507.10	12,193.83	30,598.75	39,506.64	50,017.73	56,691.84	71,048.35
Mean Reserve growth rate	N/A	5.97%	21.76%	29.11%	15.50%	13.34%	-1.10%	517.43%
Minimum	23.01	9.85	46.62	40.09	55.72	55.76	101.45
Minimum growth rate	N/A	-57.19%	-0.52%	-14.02%	39.34%	0.08%	20.28%	340.89%
Median	960.58	1,152.68	2,557.59	3,308.85	3,809.75	3,876.71	4,792.08
Median growth rate	N/A	20.00%	27.12%	29.37%	15.41%	1.76%	0.39%	398.87%
Maximum	3,54,902	3,95,155	10,68,490	15,30,280	24,16,040	28,66,080	38,59,170
Maximum growth rate	N/A	11.34%	28.07%	43.22%	23.95%	18.63%	0.51%	987.39%
Standard deviation	34,317.80	38,423.60	1,14,911.00	1,51,177.48	2,14,034.42	2,48,612.87	3,29,672.30
Data source: IMF WP/08/11 and authors’ calculations; Growth rates are based on previous year data; some years not shown

To determine the relationship between reserves (dependent variable) and its proposed determinants, we have utilized three tests: The Augmented Dickey Fuller (ADF) unit root technique examines the stochastic properties of the variables; the Granger Causality technique, tests the short run relationship between the variables; and the two stage least square method, estimates the long run relationship between the dependent and independent variables. The analysis begins with the ADF test which runs the following model by adding lagged values of the dependent variable:

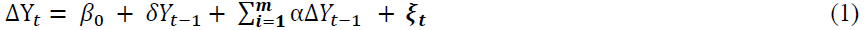
The ADF assumes that ξ_t is a serially uncorrelated error term and test the null hypothesis that δ=0. In addition, Granger and Engel (1987) suggest that two variables (Y_t and X_t ) are cointegrated if they share similar stochastic trends. Similar stochastic trends means their difference (ξ_t) is stationary and the variables never diverge too far from each other and therefore exhibit a long term equilibrium relationship (Hill et al., 2001).

Next, we test the short run relationship between the dependent and proposed explanatory variables. We apply the Granger Causality test on the time series to see how much of a current variable X_t can be explained using historical values of X_t-1. The Granger model is written as follows:

The predictive power of a variable is measured using the F-statistics, which are reported on Table 3. Additionally, we utilize residuals derived from a linear estimation of the dependent and independent variables (ordinary least square estimates), to test for co-integration using the ADF tests. Lastly, we follow authors such as Aizenman and Lee (2008) and Cheung and Ito (2009) and model the demand for foreign currency reserves as a function of the traditional view (buffer stock/precautionary variables: CA, GDP, DR, POP); monetary view (financial variables: BMGDP, Crisis); and the contemporary view (mercantilist variable: REER). This study examines two new relationships: The law of proportionate effect which is added to the regression equation (3) using a lagged value of the dependent variable and the law of least effort which is examined graphically. Specifically, we estimated the model:

Table 3: Panel Unit Root And Co-Integration Tests Of The Variables In The Model In First Difference And Granger Causality Test
Panel Unit Root Test?ADF (levels)				Granger Causality Test X Granger Cause Y
Variables	Statistics	Probability	Observations	F-Stats	Probability	Observations
RES	715	0	1503
Gibrat’s Law	2020	0	1501	5.192	0.006	357
GDP	725	0	1505	8.706	0.0002	357
DR	923	0	1486	9.2	0.0001	357
CA	896	0	1501	5.589	0.0041	357
BMGDP	909	0	1292	2.214	0.1108	357
REER	693	0	1496	6.45	0.0018	357
POP	323	0	1505	9.116	0.0001	357
Crisis	770	0	1505	3.3377	0.0366	357
Co-integration Tests ADF	344	0	356

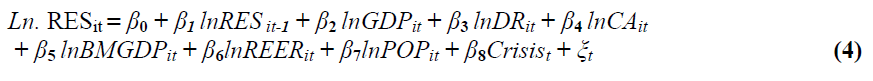
Where RES_it is the actual reserve holdings at time t and RES_it-1 is the variable of interest in this model and represents the size of the reserve in the previous period (Gibrat’s law). Audretsch et al. (2004) suggests that If β₁ is=1, then the current reserves RES_it and the initial size RES_t-1 are independently distributed and Gibrat’s Law holds. But if the coefficient is less than 1, this means that countries with smaller reserves have a tendency to accumulate reserves at a faster rate than countries with a larger pool of reserves (i.e., countries with larger reserve pools grow slowly), while coefficients greater than 1 suggest that countries with larger pools of reserves accumulate reserves at a faster rate. So, when β₁ is greater than or less than 1, then Gibrat’s Law does not hold. The other variables include: GDP which represents the size of the economy; DR is the opportunity cost of reserves, CA is foreign trade; BMGDP is the money supply in circulation; REER is the impact of exchange rate depreciation; POP serves as a scaling factor to also capture the size effects and Crisis represents the 2007-2009 financial crisis and ξ is the error term which is independent of RES_it-1. To remedy potential serial correlation and endogeneity problems we utilize the two stage least squares techniques with instrumental variables.

Furthermore, we hypothesize that countries utilize the “least effort” (Zipf’s law) to determine their level of reserves and test this proposition with a rank-frequency graph. Janicki and Prescott (2007) suggest that a power law distribution plotted on a log scale has a more valuable property that the slope follows a linear pattern. We estimate Zipf’s as:

Where R_it is the rank of each country at time (t). If =1 then Zipf’s law holds.

Results

The test of the stochastic property of the variables in the model using the ADF tests fails to reject the null hypothesis of a unit root amongst the variables in levels. Moving from levels to first difference, we were able to reject the null hypothesis of a unit root (Table 3), implying that the series are integrated in the order I (1). Table 3 also reports the results of the test of a short run relationship between the dependent and independent variables using the Granger Causality test. The results suggests that we can reject the null hypothesis that the independent variables do not granger cause the dependent variable. All the independent variables (except current account) are statistically significant at the 1% level. The last preliminary test utilizes residuals derived from a linear estimation of the dependent and independent variables (ordinary least square estimates) to test for co-integration using the ADF tests (Table 3). The series were found to be first difference stationary and integrated in the order I (1) which allows us to proceed with estimation of the model using techniques suitable for panel data.

Table 4: Determinants Of International Reserves
Variables	All Countries	Advanced countries	Emerging developing ?EMDC	Asia-Pacific Countries
Log Gibrat's Law	0.4253 (4.25)	0.4883 (4.99)	0. 4981 (4.09)	0.5860 (3.39)
Log GDP	0.3222 (4.46)	0.0382 (1.68)	0.3764 (3.89)	0.5791 (2.09)
Log DR	-0.0055 (-2.54)	-0.0505 (-3.80)	-0.0080 (-3.40)	-0.0647 (-1.81)
Log CA	0.1668 (6.60)	-0.0051 (-0.31)	0.1599 (4.86)	0.0269 (0.93)
Log BMGDP	0.4462 (5.08)	0.8861 (4.39)	-0.0104 (-0.56)	-0.0745 (-0.35)
Log REER	0.2663 (1.52)	0.2328 (1.711)	0.0949 (0.49)	-1.050 (-1.99)
Log POP	0.1186 (3.73)	0.0237 (0.11)	0.0564 (1.28)	2.550 (1.58)
Crisis	-0.0668 (-0.81)	-0.0015 (-0.04)	-0.0103 (-0.09)	0.0955 (1.38)
Adjusted R-squared	0.9	0.98	0.91	0.99

The results of the tests of equation (4) are shown in Table 4. For all countries (column 1) we find all the variables (except for the crisis dummy) statistically significant at the 1% and 5% significance level. We find that size does matter. All the variables representing size in the model have the expected sign and are significant. Beginning with the variable of interest-the size of prior year reserves is<1, rejecting Gibrat’s Law which states that the current size of reserves and initial size are independent. According to Audretsch et al. (2004), a coefficient<1 implies that countries with smaller reserve holdings have a tendency to grow their reserves at a faster rate (than larger reserve holders) in the following years. In line with apriori expectations, the size of the economy (GDP) and the size of the population (scaling factor) also matter. They are both positively related to reserves, implying that richer and more populated countries tend to trade more and hold more reserves. The deposit interest rate variable is negative, suggesting that as domestic interest rates rise, the opportunity cost of holding reserves increases, causing the central bank to hold less reserve. For all countries, the current account variable is positive, implying that more foreign trade increases the need to hold reserves to buffer market imperfections. Interestingly, the real effective exchange rate is positive and insignificant, but it is expected that currency appreciations increase the need to hold more reserves for import purposes. The money supply in circulation is positively correlated to reserves, suggesting that as the money supply in the economy increases (assuming money supply>money demand) the increased funds are being used to purchase foreign currency reserves (Obstfeld et al., 2010). The crisis variable is negative, signifying that during crisis periods, reserves get depleted, but it is insignificant.

On Table 4, we further examine the behavior of the variables in the model by their aforementioned regional classifications. The economic fundamentals in the model behave the same for the advanced countries as in the “all countries” sample except for the current account, which is negative and insignificant. Switching from advanced countries to developing countries, (EMDC sample); all the fundamentals exhibit the same signs as in the “all countries” sample, except for the money supply variable, which is negative and insignificant in the EMDC. Comparing the EMDC and the advanced countries, we find more sensitivity of the EMDC to potential market fluctuations, as they seem to hold more buffer stock reserves. The current account variable is positive and significant for the EMDC but negative and insignificant for the advanced countries. A positive relationship between the current account and reserve holdings in the developing countries suggest that these countries may be using their excess export receipts to buy foreign exchange reserves. Additionally, unlike the advanced countries, the money supply variable is negative and insignificant for the EMDC. By and large, the coefficients of the EMDC and the Asia-Pacific region seem to behave the same, except for the REER and the Crisis variables. The REER coefficient in the Asia-Pacific region has a different sign from the other three groups. It is negative and significant supporting the contemporary view (mercantilist motivation) that some of the countries in the region use reserves to buy domestic currency to prevent an appreciation (export promotion strategy).

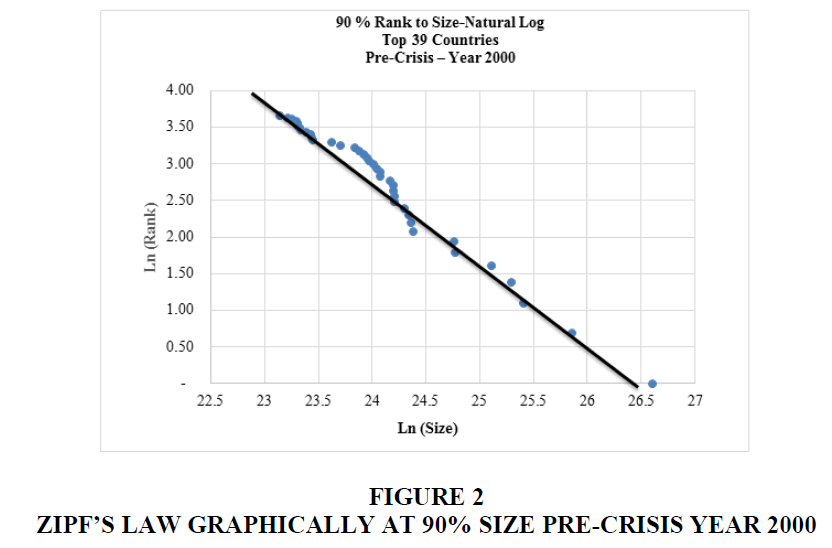
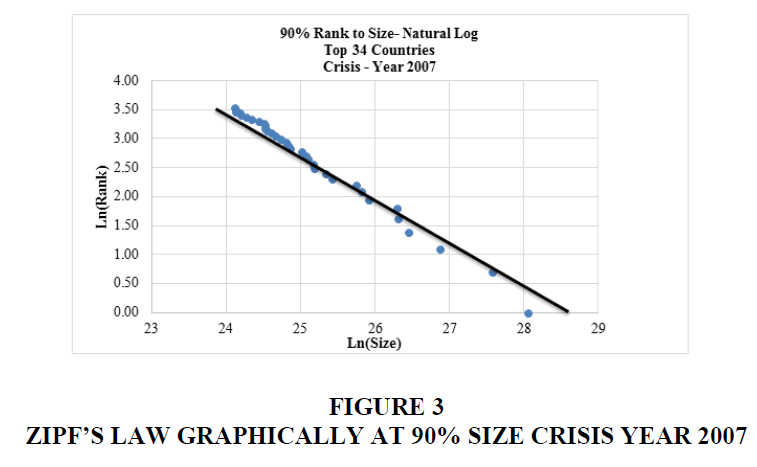
The results of the tests of Zipf’s Law are shown in Figures 2 and 3 and all confirm that Zipf’s Law holds with the downward-sloping linear relationship at the 90% rank (or the top 33 to 39 countries) during different periods. Janicki and Simpson suggest that if a Zipf’s plot is linear, it increases its predictive power. So, on Table 5, we attempt to use Zipf’s Law (Least Effort) and other existing reserve adequacy benchmarks (4% of GDP and 100% of short term debt) to forecast current reserve holdings.

Table 5: Comparison Of Reserve Balances Using Different Calculation Methods Top 10 Countries, Ranked By 2014 Reserves (Excluding Gold) (In Billions, Us $)
Rank	Country	2014 Reserves	IMF Benchmark 4% of 2014 GDP	World Bank Benchmark 100% short-term debt	Zipf's Law predictive value based on 2014 reserves*
1	China	3,859.17	414.4	1,239.45	--------
2	Japan	1,231.01	184.06	23,578	1,929.58
3	Saudi Arabia	731.92	29.85	NA	1,286.39
4	Switzerland	505.46	28.04	245.36	964.79
5	Brazil	360.97	93.84	58.18	771.83
6	Korea, Rep.	358.79	56.42	437.51	643.19
7	Russian Federation	339.37	74.42	61.75	551.31
8	Hong Kong SAR, China	328.44	11.64	111.7	482.39
9	India	303.46	81.94	85.57	428.79
10	Singapore	256.64	12.31	1,087.30	385.92
Source: International Debt Statistics 2017 and authors calculation of short-term debt as a % of GDP from other sources NA: Not Available; * Estimated as Highest reserves multiplied by 1/rank

Using 2014 reserves levels for the top ranked 10 countries, we find none of the measures appropriate in predicting current reserve levels. The IMF adequacy measures underestimate all 2014 reserve levels, the World Bank’s measure produces mixed estimates (i.e., 70% are underestimated and 30% overestimated) and with Zipf’s Law they are overestimated.

Conclusion

This study shows that “Gibrat’s Law of Proportionate Effects” (Gibrat’s Law) does not hold in the accumulation of foreign currency reserves, implying that the size of the reserve in the prior period is not independent of the growth rate, but appears to influence the growth rate in reserves. With regards to Zipf’s Law (or the Principle of Least Effort), we find that the law holds as there is an inverse relationship between the size of the largest amount of reserves and the country’s rank from the advanced and developing country views. Based on these results, we further test the predictive capabilities of Zipf’s Law to forecast foreign currency reserves holdings for the top ranked 10 countries, but find it weak. Interestingly, we also find the forecasting capabilities of IMF and World Bank adequacy measures insufficient. By and large, the findings of this paper that Gibrat's Law does not hold and Zipf's law holds, contributes to the literature with additional supports to the notion that the determinants of the demand for foreign currency reserves are dynamic and includes a myriad of quantifiable and unquantifiable factors which no single model (benchmark) can completely capture.

Our suggestion is that future research needs to emphasize reserve mitigation and management vehicles. In terms of mitigation, mechanisms for reducing global uncertainties, which precipitate the hoarding of excess reserve, need to be investigated. International financial institutions such as the IMF could be instrumental in spearheading multinational discussions on country or region specific market imperfections and risks and how to reduce their impact on the demand for reserves. In addition, given that reserve hoarding is not likely to decline soon, nations with excess reserves need to be encouraged to diversify the currencies and securities in which they hold their reserves.

Endnotes

1. Some recommended benchmarks: 4% of GDP, three months of imports, 20% of M2 or 100% of short term debt.

2. Victor Shevchuk (2015) page 103

3. Sumlinski’s empirical working paper is the only one that was found. Numerous studies have investigated the applicability of Gibrat’s Law and Zipf’s Law on growth rates of countries and cities but not international reserves.

4. Malevergne, Saichev and Sornette (2013), Page 28

5. Malevergne et al. (2013), Page 28

6. Sample of countries available upon request. Regional groups based on World Economic Outlook Database 2016.

References

1. Aizenman, J. & Lee, J. (2008). Financial versus monetary mercantilism-long term view of large international reserve hoarding. World Economy, 31, 593-611.
2. Anne-Laure, Deatte & Fouquar, J. (2012). Le retour de motifs mercantilistes dan la demande de reserves internationales de pays emergent. Revue Economique, 63, 1013-1023.
3. Audretsch D.B., Klomp L. & Thurik A.R. (2004). Gibrat's law: Are the services different. Review of Industrial Organization, 24, 301-324.
4. Bakucs, L.Z. & Ferto, I. (2009). The growth of family farms in hungary. Agricultural Economics, 40, 789-795.
5. Benguigui, L. & Blumenfeld-Lieberthal, E. (2011). The end of a paradigm: Is Zipf?s law universal? Journal of Geographical System, 13, 87-100.
6. Charles-AnyaoguNneka, B. (2012). External reserves: Causality effect of macroeconomic variables in Nigeria. Kuwait Chapter of Arabian Journal of Business and Management Review, 1(12), 8-12.
7. Cheung, Yin-Wong, & Hiro, I. (2009). Cross-sectional analysis on the determinants of international Reserve accumulation. International Economic Journal, 23(4), 447-481.
8. Choi, B.P. (2010). The US property and liability insurance industry: Firm growth, size and age. Risk Management and Insurance Review, 13(2), 207-224.
9. Eeckhout, J. (2004). Gibrat?s law for all cities. American Economic Review, 1448.
10. Frenkel, Jacob, A. & Boyan, J. (1981). Optimal international reserves: A stochatic framework. Economic Journal, 91, 507-514.
11. Higgins, M. & Klitgaard T. (2004). Reserve accumulation: Implication for global capital flows and financial markets. Current Issues in Economics and Finance, Federal Reserve Bank of New York, 10(10).
12. Hill, C., Griffiths, W. & Judge, G. (2001). Undergraduate econometrics 2nd edn. Wiley Publishers.
13. Janicki, H. & Prescot, E.S. (2006). Changes in the size distribution of US Banks: 1970-2005. Federal Reserve Bank of Richmond Economic Quarterly, 92(4), 291-316.
14. Lee, Y. & Hsu, C. (2014). Business size extension and Zipf?s law: The case of top corporate groups in Taiwan. International Journal of Business and Management. 9(4), 124-130.
15. Malevergne, Y., Saichev, A. & Sornette, D. (2013). Zipf?s law and maximum sustainable growth. Journal of Economic Dynamics & Control, 37, 1195-1212.
16. Mundel R. (1971). Monetary theory: Inflation, interest and growth in the world economy. Goodyear Publishing, Pacific Palisades, CA.
17. Nassar, I., Almsafir, M., Al-Mahrouq, M. (2014). The validity of Gibrat?s law in developed and developing countries (2008-2013): Comparison based assessment. Procedia-Social and Behavioral Sciences, 129, 266-273.
18. Obstfeld, M., Shambaugh, J. & Taylor, A. (2010). Financial stability, the trilemma and international reserves. American Economic Journal, Macroeconomics, 2(2), 57-94.
19. Pringle, R., Carver, N. (2012). RBS reserve management trends 2012. In: Pringle, R. and Carver, N. (Eds.) Incisive Financial Publications Ltd, London.
20. Scrichander, R. (2008). Financial cost of reserves. BIS Quarterly Review, 45-55.
21. Sumlinski, M., (2008). International reserves-too much of a Zipf?s thing, International Monetary Fund.
22. Williams, V.M. (2005). Foreign exchange reserves-how much is enough? Twentieth annual brown memorial lecture delivered by Dr. Marion V. Williams, Governor of the Central Bank of Barbados, at the Central Bank of the Bahamas, Nassau.
23. Zipf's, G.K. (1949). Human behavior and the principle of least effort. England: Addison-Wesley Press XI.