Citation Information: Pillay, S. (2020). Determining the optimal ARIMA model for forecasting the share price index of the Johannesburg stock exchange. Journal of Management Information and Decision Sciences, 23(5), 527-538.

Keywords

Autoregressive Integrated Moving Average; Share Price Index; Share Price Forecasting.

Introduction

The financial market plays a significant role in the economy of every society. This is explicated through the process of financial intermediation, whereby the financial market efficiently facilitates the flow of savings, capital and investments between the demand and supply sides of the real economy (Durand, 2017; Akinsola, 2018). As a system that enables the financial intermediation process, the financial market is made up of several institutions such as banks, insurance companies, financial services institutions, and regulatory agencies etc. that offer and regulate a plethora of financial products and services that are available to both lenders and borrowers (Greenbaum et al., 2015; Durand, 2017).

Amongst the plethora of financial products that are available in the financial market are shares. Also known as equities or stocks, a share is a unit of ownership of a company. Depending on the legal form of the company, shares can be traded and easily exchanged among buyers and sellers on a stock exchange (Bogle, 2017). The Johannesburg Stock Exchange (JSE), as an exchange, offers buyers and sellers the platform to buy and sell shares of companies that are listed on the exchange. This platform offers several benefits to the real economy of South Africa as it provides liquidity to companies, facilitates savings and investments in South Africa and transparency to market participants, which enables them to make informed financial economic decisions (Esterhuyse & Wingard, 2016).

When investing in the stock market, making sound economic and financial decisions remains the core focus of every investor and market participant. While this objective involves the application of skills, information and some technical prowess, the ability to predict the future performance of a stock or market index remains a veritable skill that is sought after by many market participants. In this bid, several time series models have been developed and improved over the years by notable financial economists, mathematicians, and statisticians (Rajput & Bobde, 2016). These models are often subjected to testing and validation in different empirical contexts for their predictive potential.

This study sought to test, validate, and determine the best autoregressive integrated moving average (ARIMA) model for forecasting the share price index of the JSE.

Study Problems, Significance and Objectives

Stock index forecasting is an integral component of investment finance in order to optimize returns for shareholders and equity traders. However, there have been no extensive studies performed in developing an accurate predictive model for the JSE which remains the largest stock exchange in Africa and the 19^th largest stock exchange in the world (JSE, 2020). The study thus attempted to solve this problem by determining the optimal predictive model for the determining the value of the JSE.

Given the significant market capitalization of the JSE, the optimal ARIMA could result in investors making highly profitable investment decisions in the JSE. These decisions could result in optimal returns for shareholders and thus be regarded as an efficient allocation of capital funding.

The primary objective of the study was to determine the optimal ARIMA model for predicting the JSE index prospectively. A secondary objective of the study was to utilise the optimal ARIMA model to forecast the future value of the index in the short term (22 months ahead).

Literature Review

Paul et al. (2013) sought to determine the best ARIMA model for forecasting the average daily share price indices for shares of a pharmaceutical company in Bangladesh. To select the best ARIMA model, their study utilized AIC, SIC, AME, RMSE and MAPE as the selection criteria. Upon testing several models, the study found ARIMA (2, 1, 2) to be the best model for forecasting the shares of the pharmaceutical company. Likewise, (Wahyudi, 2017) attempted to predict stock price volatility of equities that are listed on the Indonesia Stock Exchange using the ARIMA model. Whilst using the Indonesia Composite Stock Price Index, results of the empirical analysis evidenced that the best ARIMA model was (0, 0, 1). This model was determined based on the AIC criterion.

Also, from an agricultural perspective, (Jadhav et al., 2017) applied univariate ARIMA techniques to forecast and validate farm prices of cereals in Karnataka state, India. Upon analysis, the study made pragmatic findings that suggested that the ARIMA model is empirically applicable for forecasting and validating farm prices of cereal crops. Similarly, (Fattah et al., 2018) sought to model and forecast the sales demand for the products sold by a food company, using a time series approach. The study which utilized past demand information of customer purchases, tested several ARIMA models to forecast and anticipate future demand. Based on the AIC, SBC, maximum likelihood and standard error criteria, the study found the ARIMA (1, 0, 1) as the best model to predict future demand for food products of the company.

From a macroeconomic perspective, (Abonazel & Abd-Elftah, 2019) sought to develop an appropriate ARIMA model to forecast and validate the Egyptian annual gross domestic product (GDP). Upon utilizing the Box-Jenkins approach, the researchers noted the ARIMA (1, 2, 1) as the most suitable model for forecasting and validating Egyptian annual GDP. Alsharif et al. (2019) utilized ARIMA models for both daily and monthly solar radiation in Seoul, South Korea, using solar radiation data. Through a critical empirical analysis, the findings of the study suggested that while ARIMA (1, 1, 2) model can be used to predict daily solar radiation, ARIMA (4, 1, 1) model can be effectively used to predict monthly solar radiation.

Eke (2019) asserted that the ARIMA (2, 0, 3) is the best fit model for predicting the Nigerian Stock Exchange monthly stock market returns over a ten-year period. This assertion was based on the use of the Box-Jenkins technique, as well as the AIC and MSE performance criteria. In a similar study, (Mustapa & Ismail, 2019) sought to develop an appropriate ARIMA model that best fits the S&P 500 monthly stock prices for a 17-year period to enhance portfolio and investment decision making. Upon testing several models, the study found the ARIMA (2, 1, 2) and GARCH 1, 1 as the most appropriate models for predicting the S&P 500 monthly stock prices.

At the early period of the Covid-19, (Alzahrani et al., 2020) sought to forecast the daily increases of cases in Saudi Arabia and the possibility of the Umrah & Hajj Pilgrimages 2020. The researchers utilized four different prediction models: the AR model, MA model, ARMA model and ARIMA model. Upon testing all models, the study found the ARIMA model to explicate the best predictive power amongst other models. The ARIMA model further predicted the suspension of the Umrah & Hajj Pilgrimages, 2020.

In a likewise context, (Singh et al., 2020) utilized the ARIMA model to predict the spread trajectories as well as mortalities of COVID-19 in the top 15 countries as at April 2020. The study utilized the model to forecast the spread of the virus and its associated mortalities for the subsequent two months. The findings suggested a decline in both cases and associated mortalities in China, Switzerland and Germany. However, it was predicted that countries such as the United States, Spain, Italy France and the United Kingdom will witness increases in the spread of the virus as well as its associated mortalities (Singh et al., 2020).

Data and Methodology

Data Description

The data set for the study covers the period from 1 August 2019 to 31 July 2020. This timespan represented the latest data that the author could obtain at the time of writing the paper. The data was extracted from a securities brokerage firm internet database and is considered credible. This data set contains the open, low, high, and close prices of the stock index on every Monday to Friday throughout the year. To achieve consistency, the close prices are used as a general measure of stock price of the JSE index over the period of one year. Thus, for the purpose of this study, the author obtained a total of 251 observations against all working days in the year. The stepwise methodology used in this study is outlined below:

ARIMA Model

Box & Jenkins (1976) introduced the autoregressive integrated moving average (ARIMA) model (Box & Jenkins, 1976). It is also referred to as Box-Jenkins methodology composed of a set of activities for identifying, estimating and diagnosing ARIMA models with time series data. The model is most prominent in financial forecasting (Pai & Lin, 2005; Merh et al., 2010). ARIMA models outperformed complex structural models in short-term prediction and showed efficient capability to generate short-term forecasts (Meyler et al., 1998). The future value of a variable is obtained through a linear function of some random errors and some past observations of the variable, expressed as follows:

Or equivalently by

Where L is a lag operator; y_t is the actual value (i.e. stock price of JSE index) at time t; ε_t is the random error at t; c is the intercept or constant; θ_t (i = 1, 2, .... q) and α_j (j = 1, 2, …p) are the model parameters; q and p are integers and are often referred to as MA and AR orders of the model, respectively. The assumption regarding the random errors ε_t is that they are identically and independently distributed with a mean zero and constant variance of σ².

Steps to ARIMA modelling

Applying an ARIMA model to a time series data involves the following steps: visualize the time series to determine if the time series is stationary; if it is not stationary apply differencing to the time series; find the optimal parameters; build the model; and make predictions. In general, the Box-Jenkins methodology uses a three-step iterative approach of model identification, parameter estimation and diagnostic checking to determine the best parsimonious model from a general class of ARIMA model.

The preliminary test for seasonality and stationarity of the data was conducted in which natural log transformation as well as differences (d) was taken. After the stationarity of the series had been attained, both the autocorrelation function (ACF) and partial autocorrelation functions (PACF) of the stationary series were employed to choose the appropriate order of the ARIMA model. The properties are set out as follows: the series exhibits an ARMA (p, q) process, if the ACF decays exponentially (either oscillatory or direct) and PACF decays exponentially (either oscillatory or direct).

At this stage, different series of ARIMA are demonstrated and their parameters α, θ and σ are estimated using the maximum likelihood method and it is supposed that the error term is independent and normally distributed. The log-likelihood function is stated as follows:

Diagnostic checking (the last step) involves assessing the validity of the fitted and identified model(s) through the possible statistically significant test on the residuals to ascertain its consistency with the white noise, e.g. the Box Ljung Q statistics (Ljung & Box, 1978). Finally, the best fitting model would be selected according to the BIC, AICc, or AIC value (Akaike, 1974; Schwarz, 1978), i.e. the model that results in the lowest value of the criteria. The parameters of the selected model are chosen with the help of maximum likelihood estimation and forecast would be made using the model of best fit. The AIC and BIC are based on the likelihood function as well as including a different penalty term, and expressed as follows:

Where n is the number of observations, k is the number of estimated parameters and maximizes the value of the likelihood function.

Forecasting

Once a model has been fitted to the data, forecast future values can be made of time series using the following model:

Where is obtained from the above mathematical model by replacing the past value of y and ε_t by their observed values ε_t by zero and the future values of y by their conditional expectation.

The accuracy of forecasts indicates how well a forecasting model predicts the selected model. Different accuracy measures are used to validate the suitability of a model for a given data set. There are several accuracy measures in the literature, such as root mean squared error (RMSE), absolute mean error (AME), mean absolute percentage error (MAPE) and mean absolute error (MAE). The mathematical expressions for MAE, MAPE, and MSE, and are

Where t the predicted response is y_t is the observed response and n is the number of observations in the data set.

Empirical Results and Discussion

Table 1 shows the summary statistics (e.g. JB statistic, kurtosis, skewness, mean, and SD) of closing price, opening price, high price, and low price. From the table it is evident that the mean and standard deviation of closing price, opening price, high price, and low price were 48, 566.8 (3487.01), 48, 568.5 (3483.05), 48,970.2 (3443.18), and 48, 104.4 (3684.36), respectively. The kurtosis values of closing price, opening price, high price, and low price are observed to be greater than 3, indicating that all of the series are leptokurtic i.e. they have thick tails, which is a common phenomenon in stock returns (Humala & Rodríguez, 2013; Mallikarjuna et al., 2017). The Jarque-Bera test showed that the series are non-normally distributed.

Table 1 Summary Statistics for Closing Price, Opening Price, High Price and Low Price
Variables	Mean	Std. Deviation	Skewness	Kurtosis	Jarque?Bera statistic (P-value)	Tsay test
Closing price	48566.84	3487.01	-1.96	4.12	313.31(0.000)	Non linear
Opening price	48568.54	3483.05	-1.96	4.16	5400(0.000)	Non linear
High price	48970.16	3443.18	-2.00	4.37	4955.7(0.000)	Non linear
Low price	48104.26	3684.36	-2.01	4.30	37.53(0.000)	Non linear

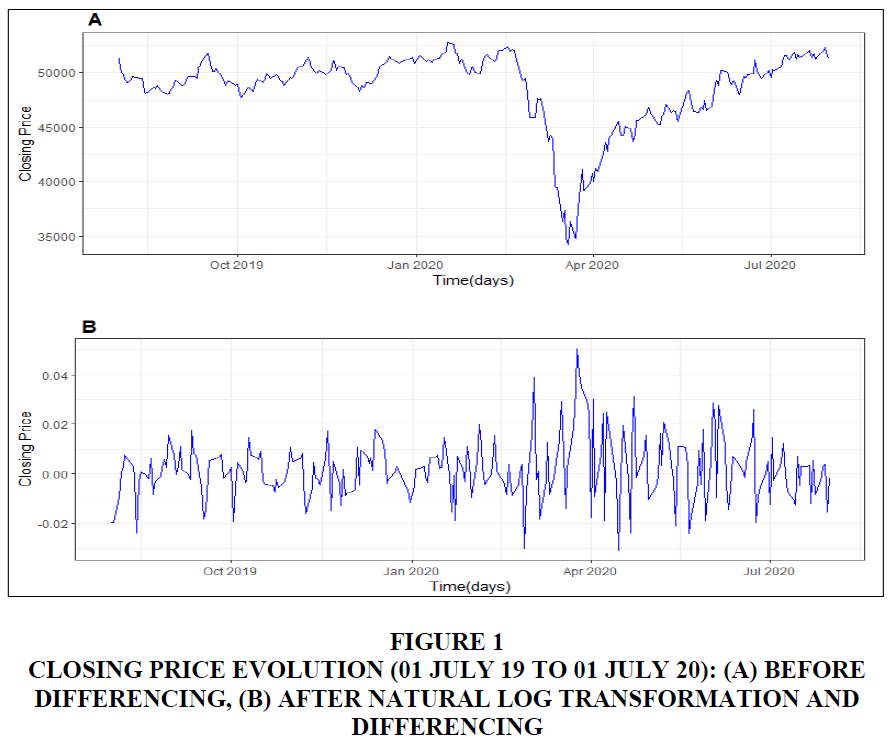
The daily values of closing price index that were used for this study are expressed in South African currency and cover the period from 01 July 2019 to 01 July 2020 which makes a total of 251 observations. Figure 1A depicts the original pattern of the series to have a general overview of whether the time series is stationary or not. From this Figure, it can be noted that the time series has a random walk pattern. Therefore, the series must be transformed for any further statistical inference. Stationarity was tested by checking the absence or presence of unit root using the Augmented Dickey-Fuller (ADF) test (Dickey & Fuller, 1979). According to the ADF test, the time series data was not stationary (the test statistic = -2.656; p-value = 0.0820). From Figure 1B (after first differencing), it is evident that the series of closing price indexes become stationary (i.e. there is no systematic increase or decrease of the trend). The Dickey-Fuller test also confirmed the stationarity of the series of closing price index after the first difference (test statistics = -11.45; p- value<0.001). Hence, after the first order of differencing and a log transformation, the time series data was more suitable for ARMA modelling.

Furthermore, after selecting a potential model and estimating its parameters, the diagnostic check was performed with the basic assumption that the residuals are a white noise process and are expected to be identically and independently distributed with zero mean and constant variance. ACF and Box-Ljung tests were used to check whether the residuals are correlated. According to Ljung-Box Q Statistics (Chi-squared statistics = 1.938; p-value = 0.7873), the study failed to reject the null hypothesis of a white noise process. From Figure 3B, it can be noted that there is no residual correlation left in the time series data set because all of the series are within the boundaries. The normal Q-Q graph of the time-series residuals falls approximately along the line (Figure 3). Therefore, the ARIMA (4, 1, 4) was successfully selected as a potential model to be used for forecasting.

After the data had been stationarised by first differencing, the next step in fitting an ARIMA model was to determine how many MA or AR terms are needed to correct any autocorrelation that remains in the differenced series. Therefore, the numbers of MA and/or AR terms that are required to fit a model are tentatively identified by looking at the PACF and ACF plots of the differenced time series. Hence, in Figure 2, the optimal lag length from the ACF plot looks to be 2 and the numbers of significant correlation lags from the PACF plot are almost 2. Therefore, the first tentative model was ARIMA (2, 1, 2) where ??=2 & ??=2 are the order of moving average (MA) and autoregressive (AR) model respectively, and ??=1 is the order of integration. Hence, a number of possible models manifest themselves. These are ARIMA (2, 1, 2), ARIMA (2, 1, 3), ARIMA (2, 1, 4), ARIMA (3, 1, 2), ARIMA (3, 1, 3), ARIMA (3, 1, 4), ARIMA (4, 1, 2), ARIMA (4, 1, 3), and ARIMA (4, 1, 4). A comparison of these models was based on their AICc, AIC, and BIC. The AIC and BIC in Table 2 show that the ARIMA (4, 1, 3) model gives the best fit to the data (i.e. improves the efficiency of the model).

Table 2 Evaluation of Arima Models
Model	AIC	BIC	ME	RMAE	MAE	MAPE
ARIMA (2,1,2)	-1005.6	-981.00	0.00047	0.01545	0.01067	0.0991
ARIMA (2,1,3)	-1003.6	-980.75	0.00031	0.01555	0.01081	0.1005
ARIMA (2,1,4)	-1004.5	-981.59	0.00037	0.01550	0.01082	0.1005
ARIMA (3,1,2)	-1004.2	-981.29	0.00032	0.01550	0.01077	0.1001
ARIMA (3,1,3)	-1007.3	-981.12	0.00033	0.01549	0.01077	0.1000
ARIMA (3,1,4)	-1006.4	-976.99	0.00044	0.01540	0.01070	0.0994
ARIMA (4,1,2)	-1003.2	-977.02	0.00033	0.01550	0.01077	0.1000
ARIMA (4,1,3)	-1010.8*	-981.39*	0.00032	0.01550	0.01077	0.1000
ARIMA (4,1,4)	-1008.9	-976.28	0.00032*	0.01527*	0.01059*	0.0984*

The potential model was further selected based on the one with least value of forecasting errors like MAPE, RMSE and MAE. For that reason, data from 01 July 2019 up to 31 August 2020 was used to fit different models. The fitted models were used to forecast one year ahead, with the purpose to see how the forecasts are close to the real data. Hence, the ARIMA (4, 1, 4) model was the one with the smallest forecasting error compared to the other models (Table 2).

Forecasting with the Fitted Models

The main objective of this study was forecasting; therefore, after successfully identifying a potential model that describes the historical data of the consumer price index of South Africa well, the same model was used also to forecast the future values in short term (22 months ahead). From Figure 4 and Table 3 it is evident that there is a persistent increase and upward trend of the South African consumer price index. The light and heavy shaded region in Figure 4 corresponds to the 95% and 80% confidence interval, respectively, of the CPI forecast values. Previous studies done in different countries also reported similar findings (Akpanta & Okorie, 2015; Norbert et al., 2016; Nyoni, 2019; Wilczek & Erlandsson, 2019), showing that an upward trend exists over the forecasted periods.

Table 3 Future Forecasts from Arima (4, 1, 4)
Dates	Forecast	95% CI
		Lower	Upper
Jan 21	51699.2	48736.5	54661.9
Feb 21	51722.5	48561.3	54883.7
Mar 21	51745.5	48384.3	55106.6
Apr 21	51765.5	48203.7	55327.3
May 21	51784.1	48021.7	55546.6
Jun 21	51803.8	47840.7	55766.9
Jul 21	51823.4	47659.3	55987.6
Aug 21	51840.9	47475.5	56206.3
Sep 21	51856.9	47290.8	56423
Oct 21	51873.5	47107.1	56639.8
Nov 21	51890.2	46923.9	56856.6
Dec 21	51905.4	46739.3	57071.5
Jan 22	51919.2	46554.1	57284.2
Feb 22	51933.2	46370	57496.3
Mar 22	51947.4	46186.8	57708.1
Apr 22	51960.6	46003.1	57918.1
May 22	51972.5	45819	58125.9
Jun 22	51984.3	45636	58332.7
Jul 22	51996.5	45454.2	58538.8
Aug 22	52007.8	45272.4	58743.2
Sep 22	52018.1	45090.6	58945.6
Oct 22	52028.2	44909.8	59146

Conclusion and Recommendations

The main objective of this study was to determine the optimal ARIMA model for forecasting the South African stock price index. The findings of the study reveal that the ARIMA (4, 1, 4) model is stable and the most suitable model to forecast the stock price index of South Africa for the next two years. Investors should thus be able to utilise the model for accurate stock price prediction and generating sustainable profits on stock investments. In general, the stock price index in South Africa showed an upwards trend over the forecasted period.

It is recommended that future studies investigate hybrid techniques to determine which incorporate the ARIMA (4, 1, 4) model to develop higher quality predictive models using recent stock prices. Based on the results, policy makers in South Africa should adopt efficient monetary and fiscal policies to reduce the increases in inflation as reflected in the forecasts. In terms of monetary policy, the South African government needs to consider lowering the money supply and interest rates to reduce inflation and in terms of fiscal policy, the government should consider adjusting income tax rates and government expenditure in order to reduce the inflation rate.

References

1. Abonazel, M. R., &amli; Abd-Elftah, A. I. (2019). Forecasting Egylitian GDli Using ARIMA Models. Reliorts on Economics and Finance, 5(1), 35-47.
2. Akaike, H. (1974). A new look at the statistical model identification. IEEE transactions on automatic control, 19(6), 716-723.
3. Akinsola, F. A. (2018). Revisiting financial liberalisation and economic growth: A review of international literature. Working lialiers 24794, University of South Africa, Deliartment of Economics.
4. Aklianta, A., &amli; Okorie, I. (2015). On the Time Series Analysis of Consumer lirice Index data of Nigeria?1996 to 2013. American Journal of Economics, 5(3), 363-369.
5. Alsharif, M. H., Younes, M. K., &amli; Kim, J. (2019). Time series ARIMA model for lirediction of daily and monthly average global solar radiation: The case study of Seoul, South Korea. Symmetry, 11(2), 240.
6. Alzahrani, S. I., Aljamaan, I. A., &amli; Al-Fakih, E. A. (2020). Forecasting the sliread of the COVID-19 liandemic in Saudi Arabia using ARIMA lirediction model under current liublic health interventions. Journal of infection and liublic health, 13(7), 914-919.
7. Bogle, J. C. (2017). The Little Book of Common Sense Investing: The Only Way to Guarantee Your Fair Share of Stock Market Returns. John Wiley &amli; Sons.
8. Box, G. E., &amli; Jenkins, G. M. (1976). Time series analysis: Forecasting and control San Francisco. Calif: Holden-Day.
9. Dickey, D. A., &amli; Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366a), 427-431.
10. Durand, C. (2017). Fictitious caliital: How finance is aliliroliriating our future. Verso Books.
11. Eke, C. N. (2019). Time Series Analysis on Monthly Stock Market Returns of the Nigerian Stock Exchange: An Arima Modeling Aliliroach. Asian Journal of Economics, Business and Accounting, 11(4), 1-9.
12. Esterhuyse, L., &amli; Wingard, C. (2016). An exliloration of the online investor relations (IR) liractices of comlianies listed on the Johannesburg Stock Exchange (JSE). South African Journal of Economic and Management Sciences, 19(2), 215-231.
13. Fattah, J., Ezzine, L., Aman, Z., El Moussami, H., &amli; Lachhab, A. (2018). Forecasting of demand using ARIMA model. International Journal of Engineering Business Management, 10, 1-9.
14. Greenbaum, S. I., Thakor, A. V., &amli; Boot, A. W. (2015). Contemliorary financial intermediation. Academic liress.
15. Humala, A., &amli; Rodr