Keywords

Earning Management, Benford Law, FSD Score, Indian Companies.

Introduction

Do Indian firms use to manipulate their earnings numbers? In earnings management, distributional approach and discretionary accrual approach had already researched this question in great detail (Carslaw, 1988; Dechow, Ge & Schrand, 2010; Dechow & Skinner, 2000; Thomas, 1989; Varian, 1972). The distribution based approach can yield a better result (Amiram, Bozanic & Rouen, 2015) whereas discretionary accrual based approach has possible biases due to various reasons (like un-observability of the actual amount of discretionary expenses, varying nature of coefficients across time, higher biases in estimation, etc.). Among the distribution based approach, the application of the law of leading digits (commonly known as the Benford Law), which states that in naturally observed numbers, lower (higher) digits always have higher (lower) chances of occurrence. Therefore, the probability of lower digits is monotonically decreasing. Globally, researchers have applied this law in testing the level of manipulation in accounting numbers to a great extent.

Recently, Amiram et al. (2015) have proposed a new measure based on the Mean absolute deviation (MAD) as Financial Statement Deviation score (FSD Score) for testing all the digits at the first place jointly. Though it is also based on Benford law, it contains better statistical properties and has better predictability powers compared to the original Benford Law. This study applies the FSD score method for assessing the levels of manipulation in Indian companies. The contribution of this study is three folds. First, it applies an innovative and better method for estimating the level of manipulations in the Indian companies. Secondly, it adopts a longer horizon of study, thereby increases the accuracy of results and show how the manipulation has changed on a yearly basis. Thirdly, it employs five number of variables compared to earlier studies which focus primarily on Net Profit (PAT) and earnings per share (EPS).

In our study, FSD score for DPS was high for all firms, by taking all negative firms and positive firms collectively and separately too. For negative firms, all five variable studies are found deviating from their Benford distributionand thus it indicates manipulation in the numbers of all year’s aggregated and individual year wise. Positive firms are found manipulating only for DPS numbers in aggregate of all years. This study is divided into six sections. The first section introduces the study, whereas, the second section is providing a brief review of the related literature of this study. The third section introduces the variables and our proposed methodology. The fourth section presents the resultsand its analysis and the sixth section concludes the finding of this study.

Literature Review

Accrual based estimation models (both cross sectional and time series) have assumed that the estimated coefficients are constant throughout the study period and do not incorporate any unobserved change and hence ultimately leading to biased results. Another problem with accrual models is that they usually depend on firm characteristics (Dechow et al., 2010; Owens, Wu & Zimmerman, 2013) whereas; distributional based measures are independent of them (Amiram et al., 2015). The distributional based measure is insensitive to any managerial motives for manipulation but captures its true level (Beneish, 1999; Dechow & Skinner, 2000). The biggest benefit of the distributional approach is its scale, independent capability and can be applied to varied setup, irrespective of currency or other unit related issues (Amiram et al., 2015). The Distribution based detection measure was first employed by Varian (1972) for economic forecast related manipulation. In Accounting literature, it was first implemented by Carslaw (1988) for New Zealand firms for showing how firms are involved in rounding up their numbers in case of not achieving their desired levels. It is replicated for US firms by Thomas (1989), showing the higher (lower) than the Benford proportion of digit 0 (9) for loss firms. Since then, many other studies have explored this method in different setup and confirm its power as a manipulation detection tool (Durtschi, Hillison & Pacini, 2004; Ley, 1996; Nigrini, 1996, 2012). There are several reasons of why the distributional approach is different from accrual based approachesand it also provides better results compared to accrual based estimates. Some of them can be discussed here. The rounding up behavior was also found different for positive and negative firms (Skousen, Guan & Wetzel, 2004).

Emerging and developing markets have also shown such rounding up manipulation behavior in accounting figures (Al-Daravseh, Hussain & Waples, 2000). Most of the studies have tested the manipulation in second digit level and applied the Benford distribution directly within an individual digit’s significance. The main approach remains here, as for whether individual digits deviate from the Benford’s distribution or not. If it deviates significantly, then the manipulation is confirmed. However, the method proposed by Amiram et al. (2015) the FSD score method is capable of jointly test the significance of all digits in the first place. Earlier studies have highlighted the need for detection of manipulation by Indian firms (Jaiswall & Banerjee, 2012). Shette and Kuntluru (2014) had applied the Carslaw in similar studies for Indian firms and confirm the manipulation in PAT and EPS figures. They have replicated the work of Carslaw for Indian firms and further analyzed the firms, based on their size of incomes (low income vs. high income), market capitalization (small vs. large), Industry, IPOs (Pre vs. Post) and Earning news (good vs. bad). They confirmed that for positive PAT firms (similar to Carslaw, 1988; Thomas, 1989), the PAT figures are manipulated in favor of higher (lower) zeros (nines) at a second digit from the left. They also find similar results for EPS for higher zero and lower nines for positive PAT firms. However, in light of the recent development of a joint test for all digits together, as proposed by FSD score, this will be an interesting research issue.

Data And Research Methodology

This study uses data from 5326 Indian firms (a representative sample of the Indian market), covering two major public stock exchanges, namely Bombay stock exchange (BSE) and National Stock Exchange (NSE) till October 20, 2017. Five variable, namely, Total revenue (Revenue), Operating profit (Operating Income), Net profit (PAT), Earnings per share (EPS) and Dividend per share (DPS) has studied annually from the financial year 1991-1992 till the financial year 2015-2016. All variable data are extracted from the Prowess database of Centre for Monitoring Indian Economy (CMIE).

For Revenue, Operating Income and PAT, the figures are available from the financial year 1990 onwards, for the majority of firms. Revenue is a figure which is a direct outcome of all expected cash flows available to firms; thereby managers’ motivation could be higher to manipulate this number. Operating Income and PAT are closely related to revenue; however, the estimation of these two numbers is also dependent on many other factors. Managers can utilize their discretion in reporting these two numbers with varied motives.

For EPS, the figures as reported under Accounting Standard-20 (AS-20) started coming more after the financial year 2000, therefore analysis for a digit at the first place conducted after the financial year 2000. In our study, we have also considered DPS as a variable which is prone to adjustments. The reason for such assumption is that dividends are sending a positive signal to investors about the profitable status of firms. DPS is also analysed after the financial year 2000.

Our research methodology is adopted from the recent study based on conformity of an observed first digit distribution within the Benford distribution. All non-manipulated accounting data are supposed to follow the Benford distribution because of central limit theorem condition. All variables first place digits are tested jointly. This is in contrast to the normal z-test conducted for individual digits at the first place or subsequent places.

The basis of the proposed methodology and how it works are explained next. The probability of any first digit beginning with d in a probability distribution function can be obtained as the area under the curve of the given distribution.

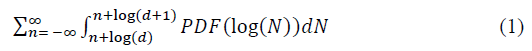
Here, in the equation, digit d at first place will follow the exact Benford law if, its area under the curve become 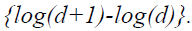It will give a very smooth and symmetric distribution in log scale (Amiram et al., 2015; Pimbley, 2014).

The main advantage of using FSD in our study is that examining a single digit individually with Benford distribution which had been doubted in earlier studies. Here, a joint examination for all digits at the first place is done using a mean value of distance for all digits from their Benford distribution. This measure is based on the Mean absolute Deviation (MAD). The mean value of the difference between a given distributions within Benford distribution for all leading digits. The calculation method for this MAD based FSD score is given as:

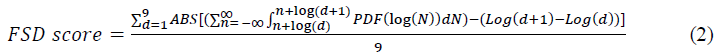
Here on the right side of equation 2, (Log(d+1)-Log(d)) is the Benford distribution value of digit d at the first place which is calculated based on logs of a number d. The remaining part of the numerator is the value of the distribution of digit d at the first place in our observed data and which is based on a natural log (log d) of a digit in numbers.

The complete theoretical underpinning of FSD Score is given in Appendix 2 of Amiram et al. (2015). Here, the interpretation is taken as smoothness and symmetry of the distribution of observed data with Benford distribution. The FSD score is based on Mean Absolute Deviation (MAD), hence unlike Kolmogorov-Smirnov (KS) test statistics, the critical values cannot be ascertained. Although, on the basis of simulation studies conducted, a value of less than 0.006 can be considered negligible and the figures can be considered following Benford distribution (Nigrini, 2012). When the observed data follows a uniform and log-normal distribution, the value of FSD will tend to zero. This shows no deviation of probabilities of a digit from Benford law, hence assumed no manipulation in the accounting figures.

Results, Discussionand Analysis

Table 1 reports the findings for the aggregated value of FSD scores for all firms year wise and for aggregated of all years together. It reports whether this aggregated empirical distribution of first digits conforms to the Benford distribution or not. The FSD score here is calculated for all first digits (1-9) together of all years and year-wise for Indian Firms. Aggregated FSD score of all years gives us a preliminary evidence of accounting numbers manipulation. Unlike FSD scores for Revenue, EPS and Operating Income the DPS is highly asymmetric and not smooth. It has a very high deviation of 0.006 (as suggested by Nigrini, 2012). It clearly hints towards a sizeable manipulation in DPS numbers of Indian firms. Moreover, on year-wise analysis also, DPS figures have shown all values greater than suggested values of 0.006 suggesting more manipulation in dividend number there. Revenue figures have shown least deviation and a better smoothing in the analysed data. Operating Income and PAT have shown a mixed result year-wise.

Table 2 reports that, the results for Negative profit firms and Positive profit firms in aggregated and year-wise. For negative firms, all five variables are showing sign of manipulation as their FSD scores and have higher deviations compared to Benford distribution. Here, DPS figures are again showing the highest level of manipulation (0.055) for all year aggregated. FSD score for DPS has increased from 0.036 for all firms taken together to 0.055 for negative firms which analysed separately. The Operating Income is the next favourite accounting numbers for manipulation. On year-wise analysis of all variables for negative firms, we find the deviation of DPS figures FSD score increased substantially from FSD scores for all firms taken in Table 1.

Table 1: Fsd Scores Of All Indian Firms
Year	Revenue	Operating Income	PAT	EPS	DPS
1990	0.009	0.012	0.01	NA	NA
1991	0.009	0.004	0.023	NA	NA
1992	0.005	0.003	0.008	NA	NA
1993	0.006	0.005	0.008	NA	NA
1994	0.004	0.003	0.010	NA	NA
1995	0.004	0.008	0.009	NA	NA
1996	0.003	0.005	0.005	NA	NA
1997	0.002	0.005	0.010	NA	NA
1998	0.002	0.009	0.007	NA	NA
1999	0.013	0.009	0.004	NA	NA
2000	0.010	0.008	0.009	NA	NA
2001	0.007	0.010	0.015	0.052	0.024
2002	0.006	0.009	0.010	0.015	0.024
2003	0.005	0.002	0.011	0.024	0.017
2004	0.007	0.006	0.012	0.011	0.016
2005	0.006	0.010	0.009	0.009	0.025
2006	0.007	0.012	0.007	0.005	0.031
2007	0.008	0.013	0.015	0.015	0.032
2008	0.008	0.006	0.009	0.008	0.028
2009	0.011	0.009	0.006	0.006	0.026
2010	0.001	0.008	0.009	0.004	0.033
2011	0.002	0.006	0.003	0.007	0.025
2012	0.003	0.007	0.003	0.002	0.022
2013	0.003	0.006	0.010	0.007	0.015
2014	0.003	0.006	0.009	0.011	0.021
2015	0.003	0.011	0.011	0.011	0.024
2016	0.003	0.006	0.006	0.005	0.017
2017*	0.005	0.012	0.005	0.005	0.019
1991-2017$	0.003	0.007	0.008	0.006	0.036

Table 2: Fsd Score For Negative Firms And Positive Firms
	Negative Firms					Positive Firms
Year	Revenue	Operating Income	PAT	EPS	DPS	Revenue	Operating Income	PAT	EPS	DPS
1990	0.022	0.029	0.030	NA	NA	0.012	0.011	0.009	NA	NA
1991	0.022	0.030	0.025	NA	NA	0.009	0.007	0.023	NA	NA
1992	0.014	0.025	0.050	NA	NA	0.007	0.003	0.007	NA	NA
1993	0.013	0.029	0.010	NA	NA	0.007	0.005	0.009	NA	NA
1994	0.015	0.023	0.018	NA	NA	0.005	0.004	0.010	NA	NA
1995	0.011	0.029	0.012	NA	NA	0.003	0.007	0.010	NA	NA
1996	0.011	0.017	0.006	NA	NA	0.003	0.006	0.005	NA	NA
1997	0.011	0.011	0.012	NA	NA	0.003	0.004	0.010	NA	NA
1998	0.005	0.007	0.005	NA	NA	0.004	0.013	0.010	NA	NA
1999	0.026	0.016	0.008	NA	NA	0.005	0.006	0.010	NA	NA
2000	0.021	0.006	0.007	NA	NA	0.006	0.010	0.010	NA	NA
2001	0.003	0.013	0.016	0.046	0.065	0.009	0.007	0.015	0.054	0.023
2002	0.011	0.012	0.013	0.029	0.033	0.003	0.005	0.009	0.014	0.025
2003	0.015	0.008	0.022	0.027	0.073	0.004	0.008	0.006	0.026	0.016
2004	0.011	0.020	0.013	0.016	0.035	0.004	0.004	0.011	0.015	0.016
2005	0.022	0.033	0.012	0.013	0.140	0.004	0.003	0.008	0.005	0.026
2006	0.012	0.020	0.019	0.022	0.149	0.004	0.008	0.004	0.005	0.031
2007	0.014	0.034	0.013	0.018	0.300	0.005	0.006	0.015	0.012	0.033
2008	0.021	0.023	0.016	0.018	0.094	0.002	0.003	0.007	0.005	0.028
2009	0.010	0.018	0.006	0.006	0.055	0.007	0.003	0.006	0.006	0.026
2010	0.018	0.018	0.018	0.005	0.098	0.007	0.006	0.007	0.003	0.034
2011	0.004	0.018	0.010	0.010	0.179	0.004	0.002	0.006	0.009	0.025
2012	0.013	0.015	0.010	0.016	0.054	0.007	0.004	0.002	0.006	0.023
2013	0.010	0.015	0.009	0.014	0.070	0.010	0.004	0.010	0.002	0.015
2014	0.003	0.010	0.019	0.013	0.033	0.004	0.005	0.005	0.006	0.021
2015	0.005	0.016	0.019	0.010	0.066	0.004	0.007	0.007	0.008	0.023
2016	0.005	0.004	0.005	0.005	0.041	0.003	0.008	0.008	0.005	0.018
2017*	0.011	0.016	0.017	0.020	0.035	0.007	0.016	0.005	0.005	0.019
1991-2017$	0.009	0.014	0.011	0.011	0.055	0.001	0.002	0.007	0.002	0.036

For positive profit making firms, FSD score of all years aggregated DPS (0.036) is very close to the FSD score reported for all years aggregated DPS (0.036). This finding corroborates the results in Burgstahler and Dichev (1997) of the higher motivation of managers for involving in earnings manipulations. We also report a monotonically increasing tendency of FSD score for loss making firms (Negative firms) compared to profit making firms (positive firms). However, for positive firms, Revenue and Operating Income report a lower FSD score (less than 0.006) which suggests a smooth distribution similar to Benford distribution. Nonetheless, all other remaining variables (PAT, EPS and DPS) show traces of manipulation for negative as well as positive firms.

Conclusion

This study examines the level of adjustments in accounting numbers for Indian firms by applying a novel distribution based approach (the FSD Score) proposed by Amiram et al. (2015). Indian firms are found adjusting DPS figures, as per the FSD scores, both on the aggregated level as well as year-wise. Loss making firms are possibly adjusting all studied variables, whereas the positive firms are adjusting mainly DPS numbers. These results are consistent with the results of Burgstahler and Dichev (1997), highlighting the motivations of loss making firms to engage in manipulation of accounting figures.

Acknowledgment

This research is supported by using a research grant from Indian Institution of Management.

References

1. Al-Daravseh, M., Hussain, I. & Waples, E. (2000). Reliability in Income numbers for investment decision: The case of the Istanbul stock market. Managerial Finance, 26(12), 26-31.
2. Amiram, D., Bozanic, Z. & Rouen, E. (2015). Financial statement errors: evidence from the distributional properties of financial statement numbers. Review of Accounting Studies, 20(4), 1540-1593.
3. Beneish, M.D. (1999). The detection of earnings manipulation. Financial Analysts Journal, 55(5), 24-36.
4. Burgstahler, D. & Dichev, I. (1997). Earnings management to avoid earnings decreases and losses. Journal of Accounting and Economics, 24, 99-126.
5. Carslaw, C.A.P.N. (1988). Anomalies in income numbers?: Evidence of goal oriented behavior. The Accounting Review, 63(2), 321-327.
6. Dechow, P.M., Ge, W. & Schrand, C. (2010). Understanding earnings quality: A review of the proxies, their determinants and their consequences. Journal of Accounting and Economics, 50(2), 344-401.
7. Dechow, P.M. & Skinner, D.J. (2000). Earnings management: Reconciling the views of accounting academics, practitionersand regulators. Accounting Horizons, 14(2), 235-250.
8. Durtschi, C., Hillison, W. & Pacini, C. (2004). The effective use of Benford’s law to assist in detecting fraud in accounting data. Journal of Forensic Accounting, 5, 17-34.
9. Jaiswall, M. & Banerjee, A.V. (2012). Exploring the relationship between earnings management and corporate governance characteristics in the Indian context (No. 704). Kolkata, India.
10. Ley, E. (1996). On the peculiar distribution of the US stock indexes’ digits. The American Statistician, 50(4), 311-313.
11. Nigrini, M.J. (1996). A taxpayer compliance application of Benford’s law. Journal of the American Taxation Association, 18(1), 72.
12. Nigrini, M.J. (2012). Applications for forensic accounting, auditingand fraud detection. John Wiley & Sons, 586.
13. Owens, E., Wu, J.S. & Zimmerman, J. (2013). Business model shocks and abnormal accrual models (No. 2365304).
14. Pimbley, J.M. (2014). Benford’s law and the risk of financial fraud. Risk Professional, May, 1-7.
15. Shette, R. & Kuntluru, S. (2014). Rounding-up in reported income numbers: Evidence from Indian companies. Review of Accounting and Finance, 13(2), 156-170.
16. Skousen, C.J., Guan, L. & Wetzel, T.S. (2004). Anomalies and unusual patterns in reported earnings?: Japanese managers round earnings. Journal of International Financial Management and Accounting, 15(3), 212-234.
17. Thomas, J.K. (1989). Unusual patterns in reported earnings. The Accounting Review, 64(4), 773-787.
18. Varian, H.R. (1972). Benfords law. American Statistician, 26(3), 65-66.