Research Article: 2019 Vol: 22 Issue: 4
Economic and mathematical modeling of loan risks for credit unions
Marek Garbowski, University of Warmia and Mazury in Olsztyn
Olga Lubenchenko, National Academy of Statistics, Accounting and Audit
Nadiia Perederii, National Aviation University
Nataliia Moskalenko, University of State Fiscal Service of Ukraine
Ihor Rumyk, KROK University of Economy and Law
Citation Information: Garbowski, M., Lubenchenko, O., Perederii, N., Moskalenko, N., & Rumyk, I. (2019). Economic and mathematical modeling of loan risks for credit unions. Journal of Management Information and Decision Sciences, 22(4), 495-500.
Abstract
The article forms the economic and mathematical models for assessing and determining the level of accumulated loan risk in the loan union. Modeling is conducted to optimize the structure of the loan portfolio of the loan union and to manage loan risk inputs. A methodological toolkit for measuring the level of loan risk concentration based on the use of homogeneous variables is developed. A loan risk management model was developed based on the analysis of the contribution of systematic factors to the total amount of loan portfolio risks.
Keywords
Economic-mathematical modeling, Degree of risk, Loan union, Task of optimization
JEL Classifications
C23, C39, G21, G30
Introduction
One of the most pressing problems today is the need to put into practice new concepts for loan risk assessment. In addition, the lack of unified approaches to the calculation of the main parameters of loan risk: the likelihood of default, losses in default and correlation of assets, the presence of positive asymmetry of the distribution of losses on the loan portfolio and the problems of excessive concentration of loan risk in the financial systems of the developing countries in the activities of loan unions.
Literature Review
The basic principles of the theory of economic risk were developed in the work (Burger & Kelly, 1993). Significant solutions to the urgent problems of quantitative and qualitative analysis of financial risks and economic and mathematical modeling of loan risks have been made in studies (Goddard et al., 2008; Ward, & McKillop, 1997; Drobyazko et al., 2019a, 2019b). The work of developing modern models of loan risk assessment and building effective risk management systems is devoted to work (Wilcox, 2006).
Methodology
The proposed approach to calculating economic capital is based on the use of a one-factor model as a tool for simulation modeling, and involves modeling LGD (default loss) as a random beta distributed variable with the possibility of considering its stochastic dependence on PD. The author proposes a method of determining economic capital based on the use of short-form and wandering defaults, which have proven themselves the best in transition economies. Assuming that PD is the default probability for one year, we show that then the probability of default over an arbitrary period of h quarters will be determined by the formula:
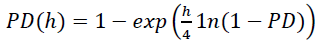 (1)
(1)
A sample of loan portfolio losses is derived from the generation of random Li variables that have a Bernoulli distribution and represent the i-loan losses in the event of the bankruptcy of the borrower (Sollenberger, 2005).
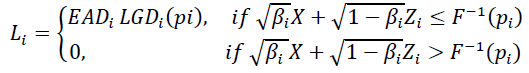 (2)
(2)
Wherein βi= coefficient of sensitivity of the yield on the ith loan to the systematic factor X, pi= the probability of default of the borrower on the ith loan, Zi ~ N(0,1)= idiosyncratic factor
Results and Discussion
We introduce a method of calculating the diversification effect, which must be taken into account by the regulator. From the Table 1, which presents the results of the allocation of credit union capital (example), shows that when applying the principle of allocation, affiliates can take advantage of risk aggregation (distributed capital Ki ≤ CTE (Xi) whereas with VαR Value at Risk) the principle is not always true, because Ki > VαR0.95 (Xi)
| Table 1 Allocation of Capital of the Credit Union (Thousand Euros) | ||||||
| Affiliate 1 | Affiliate 2 | Affiliate 3 | Affiliate 4 | Affiliate 5 | Principle of allocation | |
| VaR(i) | 1280,24 | 3694,80 | 1169,98 | 2254,98 | 1918,22 | 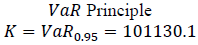 |
| Ki | 1256,90 | 3627,44 | 1148,65 | 2213,87 | 1883,24 | |
| VaR(i) | 2314,28 | 7081,70 | 2005,68 | 3989,58 | 3410,16 | 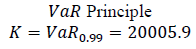 |
| Ki | 2462,54 | 7535,38 | 2134,17 | 4245,17 | 3628,63 | |
| CTE(i) | 1575,68 | 5850,10 | 1253,55 | 2601,90 | 2131,35 | 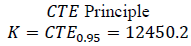 |
| Ki | 1462,62 | 5430,34 | 1163,61 | 2415,21 | 1978,42 | |
| CTE(i) | 2757,44 | 8498,04 | 2423,53 | 4856,88 | 3836,43 | 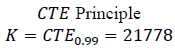 |
| Ki | 2684,19 | 8272,29 | 2359,15 | 4727,86 | 3734,52 | |
Let us define the method of conducting stress testing of the loan portfolio on the basis of multifactor models, which involves different approaches to perturbing the correlation of assets and volatility of other parameters of the model. The amount of stressful VaR loan portfolio will be determined by the formula:
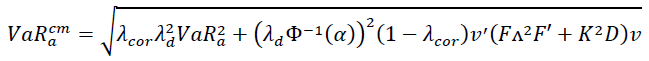 (3)
(3)
Wherein, λcor, λd, λPD are scalar factors that characterize the growth of relevant credit risk parameters, F is the matrix of the sensitivity of the return on assets to the risk factors, ν = (ν1.....νn) are specific assets of the portfolio, D and Λ are diagonal matrices, elements of which are formed from the standard deviations of the risk factors. Using this approach, it has been shown that portfolio VαR is more sensitive to an increase in the standard deviation of asset returns than to an increase in asset correlation (Esho et al., 2005). Within this approach, a toolkit for conducting stress testing of a credit union's credit portfolio has been developed for multifactor models, when the risk factors are standard and normally distributed and when they are independent.
Setting up credit risk optimization tasks at the portfolio level and solving them is a much more difficult problem than in the case of market risk. The point here is not only the lack of historical data on credit events, but also the fact that credit unions do not have a clearly defined market price, unlike securities. An important feature of these tasks is the inability to purchase a loan (investor) in a predetermined amount. The size of the loan is determined by the borrower in the loan application, based on the need for credit resources, and because of this the decision of the credit union management simplifies to determine the rate of return on the loan and is mostly binary: to issue a loan of this size or not (Sharma et al., 2009). However, we may also consider a continuous case, assuming that the credit union may partially satisfy the loan application, and the borrower always agrees. For example, if wi is the fraction of the ith application in the total amount of free credit resources of the credit union, then the problem of nonlinear two criteria binary optimization would be:
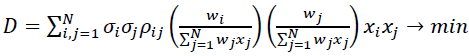 (4)
(4)
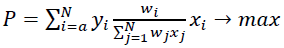 (5)
(5)
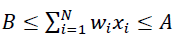 (6)
(6)
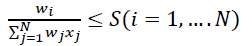 (7)
(7)
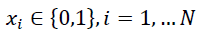 (8)
(8)
Wherein 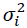 is variance in loan yields, ρij is the correlation between the yields of ith and jth loans, А,В,S are parameters that regulate, respectively, the share of free credit resources of the credit union to be used and the level of concentration of the portfolio. In this article, we propose methods for calculating loan yields yi and their dispersions
is variance in loan yields, ρij is the correlation between the yields of ith and jth loans, А,В,S are parameters that regulate, respectively, the share of free credit resources of the credit union to be used and the level of concentration of the portfolio. In this article, we propose methods for calculating loan yields yi and their dispersions 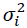 for annual repayment loans at the end of the term and for loan portfolios of arbitrary maturity loans in the form of an annuity. Using the discounted mathematical expectation formula, we find yi:
for annual repayment loans at the end of the term and for loan portfolios of arbitrary maturity loans in the form of an annuity. Using the discounted mathematical expectation formula, we find yi:
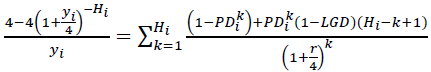 (9)
(9)
If you use the formula to determine the approximate value of the yield to pay off the loan, then the yield of the loan can be found in the following form:
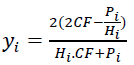 (10)
(10)
Wherein, CF are quarterly payments, Pi is the price of the ith loan, Hi is number of repayment quarters for the ith loan. The Delta method has analytically found the variance in the yield of such loans:
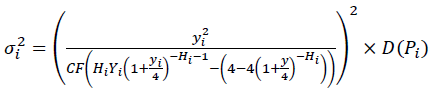 (11)
(11)
Wherein, D(P)i is variance of loan price.
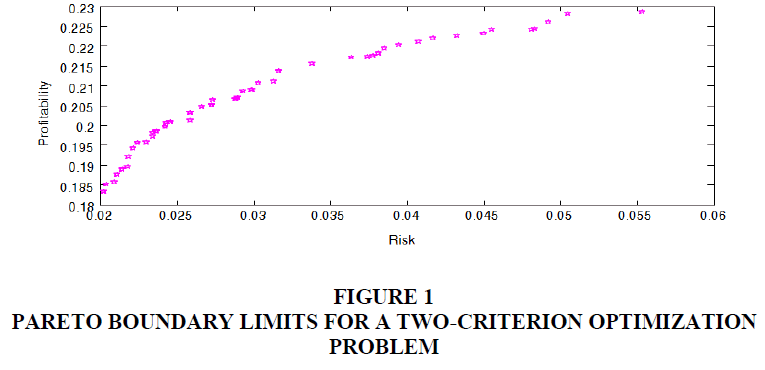
To build a set of efficient (Pareto-optimal) portfolios and Pareto boundaries, crossover and mutation operators and corresponding software have been developed that implements a genetic algorithm for solving multicriteria nonlinear binary optimization problems. Figure 1 shows Pareto boundaries for the task with two optimization criteria- risk (variance) and portfolio return (Table 2).
| Table 2 List of Loan Applications in the Credit Union | ||||||||
| No. of the borrower | Default probability, PDi | Wi | No. of the borrower | Default probability, PDi | Wi | No. of the borrower | Default probability, PDi | Wi |
| 1 | 0,05 | 0,1 | 11 | 0,15 | 0,1 | 21 | 0,25 | 0,1 |
| 2 | 0,12 | 0,05 | 12 | 0,2 | 0,1 | 22 | 0,18 | 0,14 |
| 3 | 0,15 | 0,1 | 13 | 0,05 | 0,06 | 23 | 0,08 | 0,06 |
| 4 | 0,15 | 0,14 | 14 | 0,17 | 0,1 | 24 | 0,2 | 0,1 |
| 5 | 0,2 | 0,05 | 15 | 0,15 | 0,1 | 25 | 0,25 | 0,08 |
| 6 | 0,11 | 0,1 | 16 | 0,12 | 0,11 | 26 | 0,17 | 0,1 |
| 7 | 0,17 | 0,05 | 17 | 0,18 | 0,11 | 27 | 0,25 | 0,08 |
| 8 | 0,15 | 0,07 | 18 | 0,2 | 0,13 | 28 | 0,08 | 0,13 |
| 9 | 0,1 | 0,07 | 19 | 0,15 | 0,1 | 29 | 0,18 | 0,14 |
| 10 | 0,09 | 0,05 | 20 | 0,07 | 0,05 | 30 | 0,12 | 0,21 |
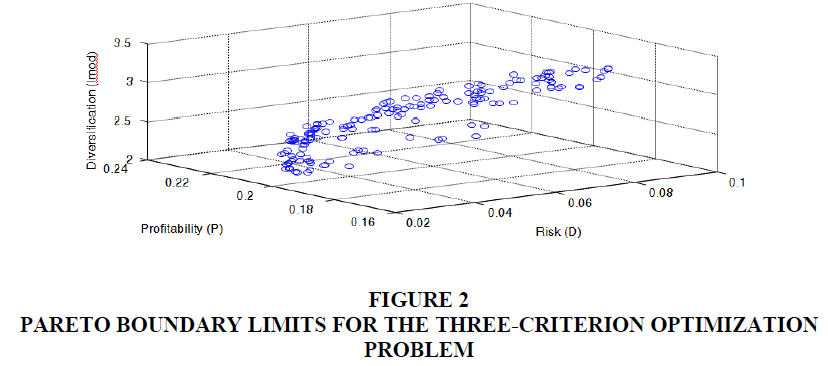
Figure 2 shows the Pareto boundary when the third criterion is added - the author's Imod index, which characterizes the concentration of credit risk of a portfolio. The paper substantiates the necessity of normalization of optimization criteria, for which the toolkit of use for problems of optimization of credit portfolio is developed, based on the analysis of these criteria within Pareto effective portfolios. (Brown & Davis, 2009).
Recommendations
The proposed models allow to take into account different types of credit union credit policy in optimizing the loan portfolio, can be applied in the credit decision making system for credit unions.
Conclusions
System of stress test models of credit risk factor concentration, based on the application of simulation and scenario modeling techniques, is built. The advantages of this approach are the ability to model perturbations of individual parameters, such as LGD default losses, to which the credit risk of a portfolio is even more sensitive than the probability of default. A number of portfolio-level signals are proposed to help warn of potential problems that may lead to credit events and to an approach to managing credit risk based on a focus on regulating the relative performance of credit unions.
References
- Brown, C., Davis, K. (2009). Caliital management in mutual financial institutions. Journal of Banking &amli; Finance, 33(3), 443-455.
- Burger, A. E., &amli; Kelly, W. A. Jr. (1993). Building high loan/share ratios: challenges and strategies. Madison: Filene Research Institute.
- Esho, N., Kofman, li., &amli; Sharlir, I. G. (2005), Diversification, fee income, and loan union risk. Journal of Financial Services Research, 27(3), 259-281.
- Goddard, J. A., McKilloli, D. G., &amli; Wilson, J. O. S. (2008). The diversification and financial lierformance of US loan unions. Journal of Banking &amli; Finance, 32, 1836-1849.
- Drobyazko, S., Barwińska-Małajowicz, A., Ślusarczyk, B., Zavidna, L., &amli; Danylovych-Kroliyvnytska, M. (2019). Innovative entrelireneurshili models in the management system of enterlirise comlietitiveness. Journal of Entrelireneurshili Education, 22(4), 2019.
- Drobyazko, S., Okulich-Kazarin, V., Rogovyi, A., Goltvenko, O., &amli; Marova, S. (2019). Factors of influence on the sustainable develoliment in the strategy management of corliorations. Academy of Strategic Management Journal, 18(1), 439.
- Sharma, H. li., Sharma, D. K., &amli; Jana, R. K. (2009). Credit union liortfolio management-an additive fuzzy goal lirogramming aliliroach. International Research Journal of Finance and Economics, 30, 20-29.
- Sollenberger, H. M. (2005). Building a consensus on loan union caliital adequacy: at the aliliroliriate level, risks are covered and comlietitive caliability is enhanced. Bank Accounting &amli; Finance, 20(5), 3-14.
- Ward, A., &amli; McKilloli, D. (1997). The relationshili between loan union objects and coolierative lihilosolihies (Working lialier). School of Management and Economics, Belfast.
- Wilcox James A. (2006). lierformance divergence of large and small loan unions. FRBSF Economic Letter, August, 1-3.