Research Article: 2020 Vol: 24 Issue: 2
Financial Return on Equity (FROE): A New Extended Dupont Approach
Pablo José Arana Barbier, Pontificia Universidad Católica del Perú (PUCP)
Abstract
The DuPont analysis was born with two elements: asset turnover and profit margin. Subsequently, financial leverage was included as a third element. However, the sustainability of a Company depends on the result of more than three financial ratios, and it is necessary not only an accounting approach, but also a financial one, which has not been defined yet. The objective of the article is to propose a new decomposition of the DuPont analysis, more extended under financial criteria to aim not only to enhance profitability, but also cash generation. The starting point is the three-element DuPont model. The analysis was conducted with data from 34 industrial companies that list publicly at the Lima Stock Exchange (Peru) from 2013 to 2018, through a multiple linear regression of the main variables defined based on the literature review. The research proposes seven elements (six statistically validated for Peru), which aim not only to contribute to accounting and financial theory, but to better decision-making. The application of the model is immediate for entrepreneurs and managers with a practical application at any business level.
Keywords
DuPont Analysis, Extended DuPont Analysis, Financial Return on Equity (FROE), Multiple Linear Regression, Return on Equity.
JEL Codes
C23; C51; M41
Introduction
Donaldson Brown not only proposed the Return on Investment (ROI) model, known as the DuPont Analysis, but also the flexible budgeting (Flesher & Previts, 2013), among other relevant contributions. According to Curtis et al. (2015), the original DuPont Analysis corresponded only to the decomposition of the Return on Assets (ROA) into two elements: asset turnover (ATO) and profit margin (PM) (Bauman, 2014). Amir et al. (2011) coincided with this partition and defined ATO as net revenue (NR) divided by net operating assets (NOA), and deepened on the definition of PM, adding the after-tax condition and reaching the same definition of net operating profit after tax (NOPAT), or earnings before interests and taxes (EBIT) times one minus the tax rate applicable (Damodaran, 2007).
The ROA leads to the Return on Equity (ROE) (Fridson & Alvarez, 2011), if an additional element is added: financial leverage (FL) (Penman et al., 2007), defined as NOA over equity (Chang et al., 2014), and that considerably enhances a company’s financial performance (Lukic, 2015; Nguyen et al., 2019). Among slightly different three-element DuPont Models, Weidman et al. (2019) considered (a) PM (net income/sales), (b) ATO (sales/total assets), and (c) FL (total assets/equity), but including all the assets in the analysis, not only the NOA. A similar model was used by Mishra et al. (2009), but instead of working with net income, the authors used gross profit. Although those accounting approximations were validated, Damodaran (2007) proposed a more financial one, focusing on liquidity through its Cash Flow Return on Capital Invested (CROCI). What remains clear is that understanding these elements makes a great difference on business results, such as Melvin et al. (2004)’s successful implementation of a computer software to teach farm business managers how to use the DuPont Analysis to enhance their decision-making.
Also, the DuPont analysis has been used to achieve several different findings, such as:
1. The prediction of future earnings (Chang et al., 2014).
2. The linkage between the ROA and productivity (Bosch-Badia, 2010).
3. The effect of certain competitive advantages over a company’s profitability (Dehning & Stratopoulos, 2002).
4. The linkage between shareholder profitability and operational and financing activities (Lim, 2014).
5. Only between profitability and the DuPont Analysis plus additional factors (Bauman, 2014).
Although the author used a two-element DuPont Model. Nevertheless, it is not yet clear which DuPont composition should be used for further analyses. How many factors should be involved? Should the accounting or financial scope be used? Which technique should be utilized to validate its components?
The objective of the study is to define how many elements an appropriate and useful DuPont Analysis should have, not from an accounting, but from a financial perspective. The study is relevant because it does not involve understanding the behavior of the ROE nor to state causality, but to define which elements correlate better with each year’s ROE to determine which ones should compose it under the proposed financial scope. Although some authors have studied the ROE’s behavior under specific circumstances, such as the linkage between the ROE, dividends and equity appreciation (Godek, 2015), or mixing the decomposition of the elements of the ROE with financial multiples such as price to earnings ratio (PER) and price to book value (PBV) (Bunea et al., 2019), the study focuses merely on the components of the ROE itself. This will let the study to concentrate not on the response from the market based on a ROE result, but on understanding the variables that shape the ROE and will serve as a powerful decision-making tool. The study will consider Weidman et al. (2019)’s model as a starting point, but will take into account Damodaran (2007)’s CROCI’s logic of its cash focus. Following most of the authors cited (Amir et al., 2011; Bauman, 2014; Curtis 2007; Jin, 2017; Lim, 2014; Lukic, 2015; Soliman, 2008; Weidman et al., 2019), the elements of the DuPont Analysis will be validated through a multiple linear regression against the financial ROE proposed. The main findings are highly relevant for the accounting and financial literature since the resulting model not only offers a more extended and explanatory model, but it also will serve as an effective management system for decision-making and will let science deepen into financial decisions in emerging markets based on the Peruvian data.
Method
A multiple linear regression was conducted for the main elements of a financial focused DuPont Analysis, or Financial Return on Equity (FROE). The information processed corresponds to the financial statements of 34 out of the 42 industrial companies that list in the Peruvian Stock Exchange, since those 34 companies provided full financial information to the Peruvian equivalent to the American Securities and Exchange Commission (SEC) (in Peru called Superintendencia del Mercado de Valores). The timeframe analyzed is from 2013 to 2018, and 160 data records were considered for the regression. The data obeys to IFRS reporting (Seay, 2014). Regarding statistical validation, three tests were conducted:
1. An adjusted R2 which should be higher than 0.70 (Véliz, 2017) for the robustness of the regression.
2. The variance inflation factor (VIF) to measure multicollinearity and accepted up to 10 (Cea, 2002).
3. An ANOVA test to discard homoscedasticity through p-values higher than 0.05 (Hair et al., 2010).
Specifically, about the R2, it also serves as a valid robustness test because the study does not seek for causality between the independent and dependent variables, but only for correlation among the elements of the FROE (Hair et al., 2010; Lukic, 2015; Véliz, 2017).
The extended model started with the three-element model used by Weidman et al. (2019), which is stated in Equation (1). The elements are (a) net profit (NP), (b) equity (E), (c) sales (S), and (d) total assets (TA).
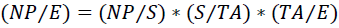 (1)
(1)
Damodaran (2007)’s CROCI involves the NOPAT adding depreciation and amortization back to it to estimate operating cash after tax. The model to be used also considers these effects, but in a different order, and considering additional elements:
1. Depreciation and amortization (D&A).
2. Earnings before interests, taxes, depreciation and amortization (EBITDA).
3. Earnings before interests and taxes (EBIT).
4. Earnings before taxes (EBT).
This model is shown in Equation (2).
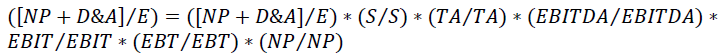 (2)
(2)
By rearranging the previous elements, a much more explanatory model is reached. It is shown in Equation 3.
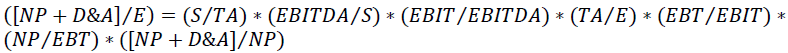 (3)
(3)
Finally, the regression to be tested took Jin (2017)’s methodology as a theoretical reference (Damodaran, 2007; Weidman et al., 2019). The regression is shown in Equation 4. Although Jin (2017) considered the dependent variable one period in the future from the rest of independent variables for its regression, the paper measured market effects, which sustain the need of the study to capture a later effect on the market. The current study focuses on the elements of the proposed FROE, all of which occur simultaneously, are extracted from the same data sources, and do not involve market information (Lukic, 2015).
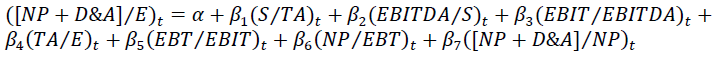 (4)
(4)
Results
The results are first presented as descriptive statistics in Table 1. In average, the FROE [(NP+D&A)/E] for industrial companies in Peru corresponds to 18.57%, which is accompanied by its corresponding components. The most relevant one is TA/E (leverage) with 1.9287 times, while the least relevant is EBITDA/S with 0.1849 times. Table 2 shows the correlations between the different elements in the multiple linear regression. Out of the 28 correlations, 17 are statistically significant at least at a 90% level. Nevertheless, none of them, except for the -0.598 between EBIT/EBITDA and (NP+D&A)/NP, exceed an absolute value of 0.50. These results are coherent with the low level of multicollinearity shown through the VIF results for each variable.
| Table 1 Descriptive Statistics | |||||
| N | Minimum | Maximum | Mean | Stand. dev. | |
| (NP+D&A)/E | 160 | 0.0130 | 1.2183 | 0.1857 | 0.2029 |
| S/TA | 160 | 0.2173 | 2.1857 | 0.8101 | 0.4489 |
| EBITDA/S | 160 | 0.0210 | 0.5184 | 0.1849 | 0.1227 |
| EBIT/EBITDA | 160 | 0.2412 | 0.9407 | 0.7611 | 0.1191 |
| TA/E | 160 | 1.0000 | 4.2272 | 1.9287 | 0.5869 |
| EBT/EBIT | 160 | 0.0398 | 3.2011 | 0.8592 | 0.3631 |
| NP/EBT | 160 | 0.1362 | 59.5969 | 1.0847 | 4.6574 |
| (NP+D&A)/NP | 160 | 1.0636 | 9.1357 | 1.8090 | 1.0762 |
| Table 2 Correlations | |||||||||
| (NP+D&A)/E | S/TA | EBITDA/S | EBIT/EBITDA | TA/E | EBT/EBIT | NP/EBT | (NP+D&A)/NP | ||
| Pearson Correlation | (NP+D&A)/E | 1.000 | 0.190 | 0.391 | 0.291 | 0.480 | 0.497 | -0.038 | -0.267 |
| S/TA | 0.190 | 1.000 | -0.464 | 0.044 | 0.062 | 0.087 | -0.062 | -0.102 | |
| EBITDA/S | 0.391 | -0.464 | 1.000 | 0.297 | 0.157 | 0.022 | -0.065 | -0.232 | |
| EBIT/EBITDA | 0.291 | 0.044 | 0.297 | 1.000 | 0.159 | 0.274 | -0.348 | -0.598 | |
| TA/E | 0.480 | 0.062 | 0.157 | 0.159 | 1.000 | 0.037 | -0.050 | -0.067 | |
| EBT/EBIT | 0.497 | 0.087 | 0.022 | 0.274 | 0.037 | 1.000 | -0.181 | -0.415 | |
| NP/EBT | -0.038 | -0.062 | -0.065 | -0.348 | -0.050 | -0.181 | 1.000 | 0.031 | |
| (NP+D&A)/NP | -0.267 | -0.102 | -0.232 | -0.598 | -0.067 | -0.415 | 0.031 | 1.000 | |
| Sig. | (NP+D&A)/E | - | 0.008* | 0.000* | 0.000* | 0.000* | 0.000* | 0.317 | 0.000* |
| S/TA | 0.008* | - | 0.000* | 0.292 | 0.218 | 0.136 | 0.216 | 0.100*** | |
| EBITDA/S | 0.000* | 0.000* | - | 0.000* | 0.024** | 0.391 | 0.209 | 0.002* | |
| EBIT/EBITDA | 0.000* | 0.292 | 0.000* | - | 0.022** | 0.000* | 0.000* | 0.000* | |
| TA/E | 0.000* | 0.218 | 0.024** | 0.022** | - | 0.319 | 0.266 | 0.201 | |
| EBT/EBIT | 0.000* | 0.136 | 0.391 | 0.000* | 0.319 | - | 0.011** | 0.000* | |
| NP/EBT | 0.317 | 0.216 | 0.209 | 0.000* | 0.266 | 0.011** | - | 0.348 | |
| (NP+D&A)/NP | 0.000* | 0.100*** | 0.002* | 0.000* | 0.201 | 0.000* | 0.348 | - | |
**Significant correlations at a 95% statistical level.
***Significant correlations at a 90% statistical leve.
After conducting the multiple linear regression, the model offered almost the minimum adjusted R2 required (Véliz, 2017), with 0.67. Table 3 shows the adjustment results. Table 4 shows
| Table 3 Adjustments for the Multiple Linear Regression | |
| Model adjustment | Results |
| R | 0.827 |
| R2 | 0.684 |
| Adjusted R2 | 0.670 |
| Table 4 Regression Results | |||||
| Variable | Type of var. | ANOVA | Coeff. | Sig. | VIF |
| (NP+D&A)/E | Dependent | 0.969 | |||
| Constant | Constant | -0.776 | 0.000* | ||
| S/TA | Independent | 0.627 | 0.179 | 0.000* | 1.402 |
| EBITDA/S | Independent | 0.986 | 0.886 | 0.000* | 1.548 |
| EBIT/EBITDA | Independent | 0.138 | 0.127 | 0.247 | 1.981 |
| TA/E | Independent | 0.512 | 0.124 | 0.000* | 1.064 |
| EBT/EBIT | Independent | 0.094 | 0.290 | 0.000* | 1.265 |
| NP/EBT | Independent | 0.380 | 0.007 | 0.003* | 1.255 |
| (NP+D&A)/NP | Independent | 0.918 | 0.033 | 0.006* | 1.969 |
1. The ANOVA tests for each variable which evidence that all of them are heteroscedastic (Hair et al., 2010)
2. The VIF tests that evidence a very low level of multicollinearity between them (Cea, 2002).
3. The constant and coefficients, all of which are statistically significant at a 99% level, except for the EBIT/EBITDA variable, which didn’t show statistical relevance.
The coefficients reflect how relevant each element is regarding the FROE’s formation (Hair et al., 2010). The variable with higher influence over the FROE was EBITDA/S, with a coefficient of 0.886, followed by the EBT/EBIT with a coefficient of 0.290. The rest of variables obtained coefficients lower than 0.18. The variable with lower influence over the FROE was NP/EBT. The only element with a negative coefficient was the constant.
Discussion
Even though Donaldson Brown’s model boosted considerably managerial decision-making (Flesher & Previts, 2013), it was only composed by the ATO and the PM (Bauman, 2014). In the same way in which an additional element can be added such as the FL (Chang et al., 2014), the resulting FROE model (Damodaran, 2007; Jin, 2017; Weidman et al., 2019) added four elements to reach a total of seven, six of which were statistically significant (Cea, 2002; Hair et al., 2010; Véliz, 2017). The model conceptually states that, in order to reach better cash approximations over equity (Kaplan & Ruback, 1995), seven ratios should be enhanced, and that obey mainly to an income statement logic.
First, the assets in which the company invests should be productive enough to let the company create value for stockholders through the generation of sales (S/TA). Although the variable reached a coefficient of 0.179, it is the starting point of the creation of value process (Richardson et al., 2010). In the particular case of the industrial companies in Peru, it obtained a mean of 0.8101, which although is not low, should invite Peruvian industrial companies to invest in more productive assets. Second, those sales should leave an important EBITDA margin through an appropriate cost and expense administration (EBITDA/S) (Aiello & Bonanno, 2013; Arana & Burneo, in press). The very relevant coefficient of 0.886 is in line with Damodaran (2007)’s CROCI, and supports the importance of cash generation inside accounting measurements beyond profitability (Bagna & Ramusino, 2017; Kaplan & Ruback, 1995). Nevertheless, in the case of Peru, it obtained a mean of 0.1849, which can be interpreted as that those companies need urgently to work on their cost and expense structure in order to offer better profits.
Third, depreciation and amortization will serve as a tax shield, as well as the rest of the cost and expense structure, but without representing a cash outflow. Nevertheless, the variable (EBIT/EBITDA) was not statistically significant. This could be due to how irrelevant depreciation and amortization are against sales, particularly in the case of Peru. Among the data, the highest proportion of those accounts against sales was of 16.98%, and the lowest of 0%, being the average 4.46%. The average EBIT/EBITDA ratio shown in the descriptive statistics is 0.7611, which should involve further analysis on which kind of assets are generating the depreciation and amortization, and how productive are those assets. This links directly with the low coefficient obtained by S/TA.
Fourth, the stockholders will leverage their results through the involvement of debt (TA/E) (Lukic, 2015; Penman et al., 2007). An important finding is that, in spite of the importance of leverage among the different DuPont models, its coefficient is 0.124, while the one for EBT/EBIT is 0.29. This could be interpreted as that the financial cost at which the company assumes debt matters more than the debt itself, regardless of the moment in which the company decides to incorporate more financial obligations (Pendar et al., 2019). It is important to consider that in emerging countries, leverage can be influenced by asymmetry of information (Huynh et al., 2020). Regarding the Peruvian industrial companies analyzed, in average the highest ratio is TA/E with 1.9287, which indicates a high financial leverage among them.
Fifth, the financial leverage involves a cost that needs to be paid and leaves the remaining profits for taxation (EBT/EBIT), and that is the one previously explained under the TA/E’s framework. The (EBT/EBIT) represents the financial expenses which, under the regression coefficients, are more relevant than debt, and in average represent 14.08% of EBIT according to the descriptive statistics in Table 1. Sixth, over the remaining profits, tax income is paid, leaving the remaining profits available for stockholders (NP/EBT). This variable got a coefficient of 0.007, mainly because every time the company is profitable, it needs to pay income taxes, in an average and relatively stable rate of 25% according to the studied companies’ data. Finally, depreciation and amortization will add cash margin for the stockholders, which means that they not only play an important role as a tax shield, but will also increase cash flow in the end ([NP+D&A]/NP) (Damodaran, 2007), although in average they represent only 4.46% of sales. Almost all of the model’s elements were statistically validated, except for the EBIT/EBITDA, although EBITDA was validated in the EBITDA/S ratio, and considering also that it serves as a good cash and company value approximation (Kaplan & Ruback, 1995).
Final Considerations
The FROE extends even more the previous DuPont models under an income statement logic with liquidity considerations under solid statistical validations. Its detailed interpretation has an important potential on managerial decision-making regarding a company’s financial results because of its extended scope, both in profits and cash, and under an income statement logic. The EBIT/EBITDA should not yet be discarded, but the model should be tested with higher amount of data and in different industries, geographies and timeframes to support its extended but innovative scope. Therefore, the main objective of the study was indeed accomplished: to propose a more extended DuPont model under a more financial scope. Finally, under the results that focus on EBITDA/S, TA/E and EBT/EBIT, decision-makers should concentrate on generating as much EBITDA as possible, and to get access to lower costs on financing sources. Without question, the sample size is indeed a limitation for the study, but in spite of that, the results are encouraging enough to replicate the study not only in different emerging markets, but in developed ones as well to consolidate the FROE as a formal theory.
References
- Aiello, F., & Bonanno, G. (2013). Profit and cost efficiency in the Italian banking industry (2006-2011). Economics and Business Letters, 2(4), 190-205.
- Amir, E., Kama, I., & Livnat, J. (2011). Conditional versus unconditional persistence of RNOA components: Implications for valuation. Review of Accounting Studies, 16(2), 302-327.
- Arana, P., & Burneo, K. (in press). Emerging market stock valuation: New evidence from Peru. International Journal of Economic Policy in Emerging Economies.
- Bagna, E., & Ramusino, E. (2017). Market multiples and the valuation of cyclical companies. International Business Research, 10(12), 246-266.
- Bauman, M.P. (2014). Forecasting operating profitability with DuPont analysis: Further evidence. Review of Accounting and Finance, 13(2), 191-205.
- Bosch-Badia, M. (2010). Connecting productivity to return on assets through financial statements: Extending the Dupont method. International Journal of Accounting & Information Management, 18(2), 92-104.
- Bunea, O.I., Corbos, R.A., & Popescu, R.I. (2019). Influence of some financial indicators on return on equity ratio in the Romanian energy sector-A competitive approach using a DuPont-based analysis. Energy, 189, 116251.
- Cea, M.A. (2002). Análisis multivariable: Teoría y práctica en la investigación social. Madrid, Spain: Editorial Síntesis. ISBN: 978-8-4773-8943-9
- Chang, K.J., Chichernea, D.C., & HassabElnaby, H.R. (2014). On the DuPont analysis in the health care industry. Journal of Accounting and Public Policy, 33(1), 83-103.
- Curtis, A., Lewis-Western, M., & Toynbee, S. (2015). Historical cost measurement and the use of DuPont analysis by market participants. Review of Accounting Studies, 20(3), 1210-1245.
- Damodaran, A. (2007). Return on Capital (ROC), Return on Invested Capital (ROIC) and Return on Equity (ROE): Measurement and Implications. Retrieved from https://www.fep.up.pt/disciplinas/mbf922/Damodaran%20-%20return%20measures.pdf
- Flesher, D., & Previts, G. (2013). Donaldson Brown (1885-1965): The power of an individual and his ideas over time. Accounting Historians Journal, 40(1), 51-78.
- Fridson, M., & Alvarez, F. (2011). Financial Statement Analysis: A Practitioner’s Guide (4th ed.). Hoboken, NJ: John Wiley & Sons. ISBN: 978-0-470-63560-5
- Godek, P.E. (2015). A simple model of market valuation and trend reversion for U.S. equities: 100 Years of bubbles, non-bubbles, and inverse-bubbles. Finance Research Letters, 13, 29-35.
- Hair, J., Black, W., Babib, B., & Anderson, R. (2010). Multivariate data analysis (7th ed.). Mexico City, Mexico: Pearson Education. ISBN: 978-0-1381-3263-7
- Huynh, T., Wu, J., & Duong, A. (2020). Information asymmetry and firm value: Is Vietnam different? Journal of Economic Asymmetries, 21(11), 1-9.
- Jin, Y. (2017). DuPont Analysis, Earnings Persistence, and Return on Equity: Evidence from Mandatory IFRS Adoption in Canada. Accounting Perspectives, 16(3), 205-235.
- Kaplan, S., & Ruback, R. (1995). The valuation of cash flow forecasts: An empirical analysis. The Journal of Finance, 4(4), 1059-1093.
- Lim, S.C. (2014). The information content of disaggregated accounting profitability: Operating activities versus financing activities. Review of Quantitative Finance and Accounting, 43(1), 75-96.
- Lukic, R. (2015). The impact of financial leverage on performance of trade in Serbia. Business Excellence and Management, 5(3), 5-21.
- Melvin, J., Boehlje, M., Dobbins, C., & Gray, A. (2004). The DuPont profitability analysis model: An Application and Evaluation of an E-learning Tool. Agricultural Finance Review, 64(1), 75-89.
- Mishra, A.K., Moss, C.B., & Erickson, K.W. (2009). Regional differences in agricultural profitability, government payments, and farmland values: Implications of DuPont expansion. Agricultural Finance Review, 69(1), 49-66.
- Nguyen, V., Nguyen, T., Tran, T., & Nghiem, T. (2019). The impact of financial leverage on the profitability of real estate companies: a study from Vietnam stock exchange. Management Science Letters, 9(13), 2315-2326.
- Pendar, M., Tayar, H., & Karimeh, S. (2019). The impact of financial flexibility on capital structure decisions: Some empirical evidence. Management Science Letters, 9(1), 133-138.
- Penman, S., Richardson, S., & Tuna, I. (2007). The book-to-price effect in stock returns: accounting for leverage. Journal of Accounting Research, 45(2), 427-467.
- Richardson, S., Tuna, I., & Wysocki, P. (2010). Accounting anomalies and fundamental analysis: A review of recent research advances. Journal of Accounting and Economics, 50(2-3), 410-454.
- Seay, S.S. (2014). The economic impact of IFRS-a financial analysis perspective. Academy of Accounting and Financial Studies Journal, 18(2), 119-139.
- Véliz, C. (2017). Análisis multivariante: métodos estadísticos multivariantes para la investigación. Mexico, D.F., Mexico: Cengage Learning. ISBN: 978-6-0732-0142-1
- Weidman, S.M., McFarland, D.J., Meric, G., & Meric, I. (2019). Determinants of return-on-equity in USA, German and Japanese manufacturing firms. Managerial Finance, 45(3), 445-451.