Research Article: 2021 Vol: 25 Issue: 6
Forecasting Malaysian Ringgit against US Dollar; Individual Models Vs Combined Models
Imam Uddin, Institute of Business Management
Qurat Ul Ain Siddiq, Institute of Business Management
Mosab I. Tabash, Institute of Business Management
Arsalan Qayyum, Institute of Business Management
Muhammad AsadUllah, Institute of Business Management
Citation Information: Uddin, I., Siddiq, Q.U.A., Tabash, M.I., Qayyum, A., & Asadullah, M. (2021). Forecasting Malaysian Ringgit Against US Dollar; Individual Models Vs Combined Models. Academy of Accounting and Financial Studies Journal, 25(6), 1-10.
Abstract
The goal of this study is to forecast the Malaysian Ringgit exchange rate against the US Dollar using individual and combined models. There are three univariate models and one multivariate model among the four individual models. ARIMA, Nave, and Exponential Smoothing are the three univariate models, and NARDL is the multivariate model. The monthly data has been taken over the period from 2011 January to 2020 December. The observations from January 2020 to December 2020 are held back for the in-sample forecasting. The findings show that the NARDL plays an important role in exchange rate forecasting and outperforms all individual and combined by the least MAPE value of 0.2066. It is also clear that the var-cor combination of NARDL and Nave outperforms three individual and other combined models with a MAPE value of 0.352. It supports Poon and Granger's (2003) argument that combining models can produce better forecasting than individual models. The findings are useful for policymakers, FOREX markets, investors, traders, tourists, and hedgers in adjusting their policies accordingly.
Keywords
ARIMA, NARDL, Forecasting, Exchange Rate, Combined Models.
JEL Classifications Code
E37, E47, F47
Introduction
Since the Bretton Woods system's demise, forecasting foreign exchange rates has become a challenging but tough job (Panda & Narasimhan, 2007; Zhang & Hu, 1998). Currency changes are simply determined by current demand and supply for imports and exports, according to the classical view (balance of payment approach). However, in the modern era, the global turnover in foreign exchange is much higher than can be explained solely by international trade.
Meese & Rogoff, (1983a, 1983b, 1988) published a series of papers in which they questioned the credibility of these monetary exchange rate models, which were subsequently withdrawn from circulation. Their empirical findings show that the models' forecasts of future nominal and real exchange rates were not as accurate as a naive random walk in predicting future nominal and real exchange rates Because the random walk model does not make use of any fundamental information, the outcome was out of the ordinary. Contrary to expectations, the random walk performed better than conditional out-of-sample forecasts, which are forecasts based on realized values of fundamentals - economic variables other than the lagged exchange rate - but do not incorporate an economic interpretation. In the years that followed, a large number of studies looked into the Meese-Rogoff conundrum with different samples, econometric specifications, and explanatory variables. Even in recent work by Cheung et al., (2003), Rossi, (2004), and others, the empirical evidence is at best mixed, and Meese-finding Rogoff's claim of poor forecasting ability (out-of-sample) of exchange rate models relative to the simple random walk has never been convincingly refuted.
In the context of Malaysian economy, the above-mentioned unsolved issue is more important due to numerous reasons. The Malaysian economy possess some interesting insights. It is small cum open economy with a floating exchange rate regime and all of them are the determinants of the economic growth of Malaysian economy. The trade openness is now one of the highest among other global economies which is approximately 200% of its GDP. In past years, approximately half of their demand relied on the external trade therefore the economic system of Malaysia is significantly vulnerable with the exchange rate risk. The government of Malaysia has exercised several exchange rate regimes which include managed floating, free floating etc. In every regime, government somehow intervene in the market which include selling small denomination of foreign currencies, buying products in domestic currencies and domestic instrument to sterilization. Therefore, in this study, we forecast the Malaysian Ringgit by applying different univariate and multivariate models individually and combinedly. The details of selected univariate and multivariate models will discuss in the later chapters.
Literature Review
In the economic domain, accurate forecasting is critical. As a result, many types of forecasting research have been conducted in recent years. Many significant techniques have been designed to improve the precision of time series modelling and forecasting. In stochastic time series modelling, the (ARIMA) is the mostly applied model (Zhang, 2007; Cochrane 1997).
Because the time series is assumed to be linear and normal in nature, this model can be used to analyze it. ARIMA models are divided into three types: autoregressive (AR), moving average (MA), and autoregressive moving average (ARMA). Autoregressive (AR) ARIMA models (Box & Jenkins, 1970; Hipel & McLeod, 1994). In addition, seasonal forecasting is used to developed by Box and Jenkins, Seasonal ARIMA (SARIMA) is a variant of the ARIMA algorithm, (1970). The ARIMA model is well-known for its time series variations and the Box-Jenkins methodology that it employs (Zhang, 2003).
Many non-linear stochastic models are employed in the literature in order to circumvent this problem (Zhang, 2003; Altavilla & De Grauwe, 2010). (ANNs) are becoming increasingly popular in the field of time series forecasting (Kihoro et al., 2004). ANNs were initially developed as a result of research by biologists, but they quickly gained popularity in the field of time series forecasting (Kamruzzaman & Sarker, 2006). ANNs do not assume the existence of a statistical distribution, and their distinguishing feature is the ability to perform non-linear modelling on their input data by default if they apply in the forecasting of any time series. In part, this is because ANNs are self-adaptive and data-driven in that the model is chosen based on the data provided (Zhang et al., 1998). An enormous amount of research and development has taken place over the last few years in the area of the application of neural networks to time series modelling and forecasting.
In the literature, there are numerous neural network structures that have been developed as a result of on-going investigation. In 1995, Vapnik developed the (SVM) concept, which completely transformed the field of time series forecasting (Suykens & Vandewalle, 1999). SVM was originally developed to solve classification problems, but it has since been applied to a variety of other tasks, including estimation, regression, and time sequence forecasting (Cao & Tay, 2003). Because of its ability to classify and generalize data, the SVM methodology is gaining in popularity in time series forecasting. A good generalization capacity rule is the primary goal of SVM, which is to apply the structural risk minimization (SRM) principle in order to identify a good generalization capacity rule (Cao & Tay, 2003). In SVM, the training data point is responsible for determining the solution to a specific problem (Vapnik, 1998).
The solution obtained by SVM differs that training is equivalent to resolving a quadratic optimization problem with linear constraints (Cao & Tay, 2003). Additional advantage of SVM is that the solution can be controlled independently of the size of the input space, which is a significant advantage (Suykens & Vandewalle, 2000; Amat et al., 2018).
Today, forecasting exchange rates is done using a combination of models, such as those used by Khashei & Sharif, (2020), who forecast using an ARIMA and an ANN model, respectively. The researchers did find that when it came to forecasting, the combined models performed better than the individual models. Lam & colleagues, (2008) looked into the major global currencies as well (Altavila et al., 2008). As a result, when it comes to forecasting, combined models typically outperform single models. Matroushi also employs two combined models, the ARIMA-ANN and the ARIMA-MLP, to forecast exchange rates in addition to the ARIMA-ANN model. In forecasting, ARIMA-MLP has been shown to outperform other combined and individual models, according to some reports (Dunis et al., 2008).
ARIMA-ANN are two combined models proposed by Matroushi, (2011) for forecasting exchange rates. He also proposed the combination of ARIMA-MLP later. The author concluded that ARIMA-MLP outperformed other combined and individual models in forecasting. Wang et al., (2016) forecasted the exchange rate by combining the ARIMA model with a three-layer ANN model. Between 2010 and 2013, data on the Euro versus the US Dollar was gathered. According to the experimental results, the proposed combined models outperform the individual forecasting techniques. Mucaj et al., (2017) used ARIMA, ANN, and the ARIMA-ANN combined hybrid model to forecast the USD/ALL time series. According to the findings, the ARIMA-ANN combined hybrid model outperforms the ARIMA and ANN models in forecasting. Amat et al., (2018) discovered that combining traditional exchange rate models with machine learning and Taylor Rule models yields more accurate forecasting estimates than single models. Zhang & Hamori, (2020) estimated the exchange rate by combining fundamental models with machine learning and comparing them to random walk models. The findings show that fundamental models combined with machine learning outperform random walk models. In previous literature, the combination of univariate time series models and NARDL is almost abundant. Recently, AsadUllah et al., (2021) forecasts the exchange rate of Pakistani Rupees against USD by combining the NARDL with different univariate time series models. The results conclude that combination of NARDL and Naïve model has outperformed other individual and combined models. Therefore, in this study, we are keen to forecast the Malaysian Ringgit against the US Dollar by applying the same combination to validate the methodology in the context of other currency i.e., Malaysian Ringgit.
Methodology
Data
From the first month of 2011, to the last month of 2019, the authors collect monthly data on the Malaysian currency, i.e. Ringgit Exchange rate against US Dollars. The remaining observations between M1 2020 and M12 2020 were saved for in-sample forecasting. The reason for choosing data from 2011 is that it is the base year of IMF IFS statistics, namely 2010, from which the authors collect all explanatory variable data in the case of the NARDL Co-Integration model. Money Base Growth Rate, Trade Balance, Gross Domestic Product, Interest Rate, Inflation Rate, Oil Prices, and Gold Prices are among the explanatory variables. The reason for selecting the above explanatory variable is evidence in the literature of a significant relationship between exchange rate and the aforementioned macroeconomic fundamentals.
Methodological Approaches
In the forecasting time series literature, there are primarily two types of models: linear and non-linear. In linear models, the model estimates future observations by considering various linear combinations of the sample, whereas non-linear models were developed to challenge and hypothesise the concept of linearity among explanatory and control variables (Khashei & Bijari, 2010).
ARMA/ARIMA
Box and Jenkins is one of the most widely used models for potential forecasting values, and it is also one of the most complex (1976). The ARIMA model estimated the future values of the time series by combining the values from the past and present. When the time series becomes stationary after the first or second difference has been taken, the ARIMA model is referred to as an integrated model. Auto regression is a mechanism that takes historical data and decomposes it into components. According to the Box-Jenkins technique, ARIMA models are written as ARIMA (a, b, c), where a denotes the order of the autoregressive model, b the order of the moving average, and c the order of the stationary model. The ARMA model is used when a time series is stationary, and it is defined as follows: (a, b).
Joshe et al., (2020) predicted the time series of the Indian Rupee/USD by employing the ARIMA model. As a result, the authors came to the conclusion that ARIMA (1,1) produced the best results. AsadUllah et al., (2020) discovered that ARIMA was also suitable for forecasting the exchange rate of the Pakistani Rupee against the United States Dollar.
Naïve
The Nave 1 model is frequently used as a comparison point for other models with similar features, such as Smoothing Exponential and ARIMA (McKenzie et al., 2002). Dunis et al., (2008) used the Nave model to calculate the US Dollar/Euro exchange rate. Newaz, (2008) ranked the Nave model seventh in forecasting the Saudi Riyal to Indian Rupee exchange rate.
Exponential Smoothing Model
The ES model (Gardner, 1985) is a widely used forecasting tool in economics and finance. According to Brooks, (2004), it is distinct from the ARIMA method, which used an earlier linear combination of the previous time series value to predict future values. The new values will be more predictive of future time series than the previous values for previous time series. In the exponential smoothing model, the ordinary model is the one-parameter exponential smoothing model, i.e., Next forecast = Last forecast + the share of the previous error.
Non-Linear Autoregressive Distributed Lag (NARDL)
Shin et al., (2014) created a non-linear ARDL model that used positive and negative partial sum decompositions to detect asymmetric effects in the long and short term. NARDL models have several advantages over classical cointegration models. For starters, they are more effective in determining cointegration relationships in small sample sizes. Second, they apply whether the regressors are stationary at the level or at the first difference (I(0) or I(1)). They cannot be used, however, if the regressors are I (2).
Le et al., (2019); Bahmani et al., (2015); Turan et al., (2018) applies the NARDL model in their studies and found that there is an asymmetric relationship between different selected variables. The explanatory variables for the analysis of NARDL are shown in below Table 1
| Table 1 Independent Variables and Their Assessments Criteria | |
| Independent Variables | Assessment Criteria |
| Money Supply | Money Stock |
| Interest Rate | Market Rate |
| Inflation | CPI |
| GDP | IPI |
| Trade Balance | Exports Subtracted By Imports |
| Foreign Reserves | Official Foreign Reserves |
| Oil Price | Crude Oil Price |
Combination Techniques
When Armstrong, (2001) examined "The combination of forecasts," he came to the conclusion that "when you are unsure which method is the best, you should weigh forecasts equally." Another fast technique proposed by Granger & Ramanathan, (1984) is a linear mixture of individual forecasts, which integrates weights from the matrix of past predictions and the vector of past observations as calculated by OLS, as well as weights from the vector of past observations. As a result, some researchers prefer to use unequal weights rather than fixed equivalent weights when conducting their research. Deutsch et al., (1994) used (STAR) models to change the fixed weights in their study, and a non-linear time-dependent weighting scheme was proposed. As a result of the foregoing, the authors incorporate the var-cor and equal weightage methods into their exchange rate forecasting calculations.
Results and Discussion
Unit Root Tests
The primary step toward analysis in case of univariate and multivariate time series is to examine the unit root of each variables. The assumption or pre-requisite of univariate and multivariate analysis is all the variables should be stationary. In case of NARDL, the variables should be stationary at level or at 1st difference otherwise either we have to drop that variable or otherwise we cannot run the NARDL model if any of variables found stationary at the second difference.
In the Table 2, it has been indicated that all variables found stationary at 1st difference except trade balance and Gross Domestic Product. The authors test the stationarity by employing ADF and PP test in order to avoid any biasedness. The above results allow the authors to successfully run the NARDL analysis as the pre-requisite has been fulfilled.
| Table 2 Unit Root Test of Exchange Rate & Explanatory Variables | ||||
| Variables | ADF Test | PP Test | ||
| Level | 1st Diff. | Level | 1st Diff. | |
| ER | -1.703 | -9.744** | -1.7035 | -9.758** |
| GDP | -1.374 | -10.538** | -12.920** | -- |
| MS | -2.293 | -9.953** | -2.667 | 10.107** |
| INF | -2.474 | -8.582** | -2.140 | -8.452** |
| IR | -2.458 | -10.340** | -2.504 | -10.341** |
| OP | -2.664 | -8.544** | -2.243 | -8.337** |
| TB | -7.247** | -- | -7.555** | -- |
| FR | -2.681 | -7.832** | -2.754 | -7.941** |
Forecasting Exchange Rate from Univariate Model
Table 3 shows the result of two univariate time series models i.e., ARIMA and exponential smoothing model. In case of ARIMA, the best fitted model is ARIMA (3,1,2) with the R-Squared, Akaike-Info & Schwarz Criterion values of 0.015078, -1.8848 & -1.7849 respectively. In exponential smoothing model, the additive model has found to be superior in case of forecasting the exchange rate. The maximum value of α indicates that the impact of historical values on recent observation dies out quickly.
| Table 3 Univariate Models Forecasting Results | ||||||
| Models | Best Fitted Models | R-Squared | AIC | SC | ||
| ARMA/ARIMA Model | ARIMA (3,1,2) | 0.015078 | -1.884856 | -1.7849 | ||
| Exponential Smoothing Model | Trend | a | ß | F | ? | A.I.C. |
| Additive Trend | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 2.713 | |
Forecasting Via Non-Linear Autoregressive Distributive Lag
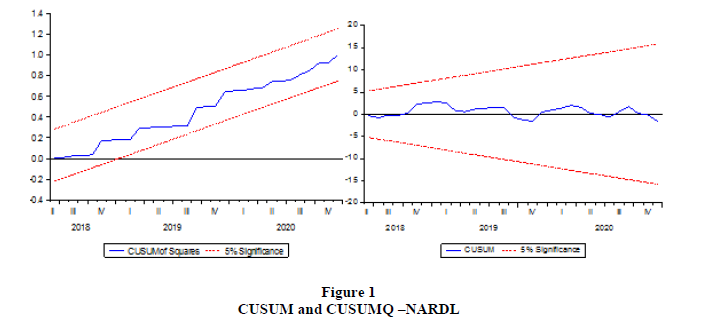
Table 4 interprets the results of NARDL analysis by employing the selected explanatory variables. The Bound test implies that there is long run-relationship at 10% significance level. The findings reveal that the Foreign reserves and exchange rate possess asymmetric relationship. One unit increase and one unit decrease in foreign reserves lead to decrease in 2.11 and increase in 3.45 units respectively which constitute the non-linear relationship between the above-mentioned variables. The decrease in exchange rate leads to enhance the exchange rate by -2.204 units which indicates that investors withdraw their investment from the economy when the return on capital declines. The diagnostic tests provide insignificant results which signifies that there is not any problem of heteroscedasticity, serial correlation and omission in the data set. The figure 1(a) and 1(b) represents the graphs of CUSUM and CUSUM-Q which implies that the NARDL is found to be stable at 5% confidence interval.
| Table 4 Nard Long Run Coefficients | ||||
| Variables | Estimates | Standard Error | T-Statistics | |
| FR-POS | -0.000049 | 0.000023 | -2.115838** | |
| FR_NEG | -0.000028 | 0.000008 | -3.453049* | |
| OP_POS | 0.007155 | 0.010645 | 0.672163 | |
| OP_NEG | 0.000752 | 0.004976 | 0.151060 | |
| IR_POS | 0.298914 | 0.618675 | 0.483151 | |
| IR_NEG | -1.238002 | 0.561700 | -2.204028** | |
| GDP_POS | -0.007618 | 0.014559 | -0.523291 | |
| GDP_NEG | -0.014665 | 0.014767 | -0.993144 | |
| GP-POS | -0.000898 | 0.000522 | -1.721103 | |
| GP_NEG | -0.000525 | 0.000574 | -0.915137 | |
| F-Statistics | R-Squared | |||
| Bound Test | 3.644032 | I0 Bound: 3.63 | I1 Bound 2.71 (10%) | |
| Diagnostic Tests | P-Value | |||
| Breusch-Godfrey LM Test | 0.1829 | |||
| Heteroscedasticity Test: Harvey | 0.1881 | |||
| RESET Test | 0.2222 | |||
**Significant at 5%
Performance of Individual and Combined Models in Forecasting Exchange Rate
Table 5 interprets the results of individual and combined models by calculating the Mean Absolute Percentage Error (MAPE). The lesser the value of MAPE, better the forecasting is the rule of thumb behind the calculation of MAPE value. In table 5, total twenty-six models have been run to forecast the exchange rate and their efficiency has been represented by the MAPE value. The twenty-six models include four individual models and eleven combined model via two, three- and four-ways permutation by applying equal weightage and var-cor methodology. The results indicate that the decision of selection of NARDL model was right as it outperforms all individual and combined models by producing the least MAPE value of 0.2066. On the other hand, it is also found that the combination of NARDL and Naïve model also found superior if compare to other individual and combined models except NARDL therefore we may conclude that the combination of different models plays a vital role in forecasting the exchange rate as combination of NARDL and Naïve outperforms other combinations and all three individual univariate models.
| Table 5 Accuracy of Individual & Combined Models (Mape Value) | ||||||||
| Individual | A | N | E | ND | ||||
| 2.353 | 1.675 | 3.890 | 0.2066 | |||||
| Equal Weightage Method | 2-Way Combinations | |||||||
| A-E | A-N | A-ND | E-N | E-ND | N-ND | |||
| 3.104 | 1.393 | 1.416 | 2.058 | 2.080 | 0.370 | |||
| 3-Ways Combination | 4-Way Combination | |||||||
| A-E-N | A-E-ND | E-N-ND | A-N-ND | A-N-S-ND | ||||
| 2.652 | 3.025 | 2.329 | 1.537 | 1.737 | ||||
| Var-Cor Method | 2-Way Combinations | |||||||
| A-E | A-N | A-ND | E-N | E-ND | N-ND | |||
| 2.807 | 1.135 | 2.701 | 1.001 | 2.471 | 0.352 | |||
| 3-Ways Combination | 4-Way Combination | |||||||
| A-E-N | A-E-ND | E-N-ND | A-N-ND | A-N-E-ND | ||||
| 1.396 | 2.564 | 0.873 | 1.003 | 1.100 | ||||
Conclusion
The objective of this study is to forecast the exchange rate of Malaysian Ringgit against the US Dollar via individual and combination of different models. The four individual models include three univariate and one multivariate model. The three univariate models are ARIMA, Naïve and Exponential Smoothing and the multivariate model represents by NARDL. The NARDL hardly applies for the forecasting of exchange rate in the previous literature therefore it is an addition in the literature. Furthermore, the combination of NARDL with the univariate time series techniques itself is a value-added for the future researchers. For the combination, the authors include the combination and equal weightage techniques to avoid the biasedness. The efficiency of forecasting is calculated by the Mean Absolute Percentage Error (MAPE). The lesser the values of MAPE, higher accurate the forecasting is. For the above objective, the data set of exchange rate, money supply, foreign reserves, interest rate, inflation rate, oil price, gold price, trade balance and Gross domestic product has been taken over the period from 2011 January to 2020 December. The observations from January 2020 to December 2020 are held back for the in-sample forecasting. The findings reveal that the NARDL plays a vital role in the forecasting of exchange rate and outperforms all individual and combined by the least MAPE value of 0.2066. It is also evident that the combination of NARDL and Naïve model under the var-cor combination outperform three individual and other combined models with the MAPE value of 0.352. It supports the argument of Poon & Granger, (2003) that the combination of models can produce better forecasting than the individual models. The results are beneficial for the policymakers, FOREX markets, investor, traders, tourists and hedgers to manipulate their policies accordingly in order to avoid any unforeseen risk and uncertainty.
References
- Altavilla, C., & De Grauwe, P. (2010). Forecasting and combining competing models of exchange rate determination. Applied Economics, 42(27), 3455-3480.
- Amat, C., Michalski, T., & Stoltz, G. (2018). Fundamentals and exchange rate forecastability with simple machine learning methods. Journal of International Money and Finance, 88, 1-24.
- Armstrong, J.S. (2001). Combining forecasts. Norwell, MA: Kluwer Academic Publishers.
- AsadUllah, M., Uddin, I., Qayyum, A., Ayubi, S., & Sabri, R. (2021). Forecasting Chinese Yuan/USD Via Combination Techniques During Covid-19. The Journal of Asian Finance, Economics and Business, 8(5), 221-229.
- Asadullah, M., Ahmad, N., & Dos-Santos, M.J.P.L. (2020). Forecast foreign exchange rate: the case study of PKR/USD. Mediterranean Journal of Social Sciences, 11(4), 129-137.
- Brooks, C. (2004). Introductory econometrics for finance. Cambridge: Cambridge University Press.
- Box, G.E., Jenkins, G.M., & Bacon, D.W. (1967). Models for forecasting seasonal and non-seasonal time series. Wisconsin univ madison dept of statistics.
- Cao, L.J., & Tay, F.E.H. (2003). Support vector machine with adaptive parameters in financial time series forecasting. IEEE Transactions on neural networks, 14(6), 1506-1518.
- Cheung, Y.W., Chinn, M.D., & Garcia Pascual, A. (2003) Empirical exchange rate models of the nineties: are any fit to survive? (Working Paper No. 551), University of California, Santa Cruz.
- Cochrane, J.H. (2005). Time series for macroeconomics and finance. Manuscript, University of Chicago, 1-136.
- Deutsch, M., Granger, C.W.J., & Terasvitra, T. (1994). The combination of forecasts using changing weights. International Journal of Forecasting, 10, 47– 57.
- Dunis, C.L., Laws, J., & Sermpinis, G. (2010). Modelling and trading the EUR/USD exchange rate at the ECB fixing. The European Journal of Finance, 16(6), 541-560
- Gardner, E.S. (1985). Exponential smoothing: The state of the art. Journal of Forecast, 41, 1-28.
- Granger, C.W.J., & Ramanathan, R. (1984). Improved methods of combining forecasts. Journal of Forecasting, 3, 197-204.
- Hipel, K.W., & McLeod, A.I. (1994). Time series modelling of water resources and environmental systems. Elsevier.
- Joshi, V.K., Band, G., Naidu, K., & Ghangare (2020), A. modeling exchange rate in India–empirical analysis using ARIMA model. Studia Rosenthaliana: Journal for the Study of Research, 12(3), 13-26.
- Kamruzzaman, J., & Sarker, R.A. (2006). Artificial neural networks: Applications in finance and manufacturing. In Artificial Neural Networks in Finance and Manufacturing 1-27. IGI Global.
- Khashei, M., & Sharif, B.M. (2020). A Kalman filter-based hybridization model of statistical and intelligent approaches for exchange rate forecasting. Journal of Modelling in Management.
- Kihoro, J., Otieno, R.O., & Wafula, C. (2004). Seasonal time series forecasting: A comparative study of ARIMA and ANN models.
- Lam, L., Fung, L., & Yu, I.W. (2008). Comparing forecast performance of exchange rate models. Available at SSRN 1330705.
- Le. H.P, Ho Hoang, G.B., & Dang T.B.V, (2019). Application of nonlinear autoregressive distributed lag (NARDL) model for the analysis of the asymmetric effects of real exchange rate volatility on Vietnam’s trade balance. Journal of Engineering Applied Sciences, 14, 4317-4322.
- Matroushi. S. (2011). Hybrid computational intelligence systems based on statistical and neural networks methods for time series forecasting: the case of gold price, Master’s Thesis, Retrieved from https://researcharchive.lincoln.ac.nz/handle/10182/3986
- Meese, R.A., & Rogoff, K. (1983a). Empirical exchange rate models of the seventies: Do they fit out of sample? Journal of International Economics, 14, 3–24.
- Meese, R.A., & Rogoff, K. (1983b). The out-of-sample failure of empirical exchange rate models: Sampling error or misspecification? In Frenkel, J.A. (Edition.). Exchange Rates and International Macroeconomics (67–112). Cambridge, MA: National Bureau of Economic Research.
- Meese, R.A., & Rogoff, K. (1988). Was it real? The exchange rate-interest differential relation over the modern floating-rate period. Journal of Finance, 43(4), 933–948.
- Mucaj, R., & Sinaj, V. (2017). Exchange rate forecasting using ARIMA, NAR, and ARIMA ANN hybrid model. Journal of Multidisciplinary Engineering Science Technology, 4(10), 8581-8586.
- Newaz, M.K. (2008). Comparing the performance of time series models for the forecasting exchange rate, BRAC University Journal, 2, 55-65.
- Panda, C, & Narasimhan, V. (2007). Forecasting exchange rate better with artificial neural network. Journal of Policy Modeling 29, 227-236.
- Rossi, B. (2005). Testing long-horizon predictive ability, and the Meese-Rogoff puzzle. International Economic Review, 46(1), 61–92.
- Shin, Y., Yu, B., & Greenwood-Nimmo, M. (2014). Modeling asymmetric co-integration and dynamic multipliers in a non-linear ARDL framework. New York: John Wiley & Sons
- Suykens, J.A., & Vandewalle, J. (2000). Recurrent least squares support vector machines. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 47(7), 1109-1114.
- Turan, T., & Mesut, K. (2018) Asymmetries in twin deficit hypothesis: Evidence from CEE countries. Ekonomický Casopis, 66(1), 580–97.
- Vapnik, V.N. (1998). An overview of statistical learning theory. IEEE transactions on neural networks, 10(5), 988-999.
- Wang. S, Tang, Z., & Chai, B, (2016). Exchange rate prediction model analysis based on improved artificial neural network algorithm. In: 2016th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 21-22 October 2016, 1-5.
- Zhang, G., Patuwo, B. E., and Hu, M. Y. (1998). Forecasting with artificial neural networks: The state of the art. International Journal of Forecasting 14, 35–62.
- Zhang, G.P. (2003). Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing, 50, 159-175.
- Zhang., Y., & Hamori. S. (2020). The predictability of the exchange rate when combining machine learning and fundamental models. Journal of Risk and Financial Management, 48(13), 1-16.