Keywords

Heterogeneous Beliefs, Asset Values.

Introduction

Equilibrium asset prices reflect investors’ beliefs about asset values. Many financial models assume these beliefs are homogeneous. Even a casual acquaintance with investment advisors and commentators suggests that belief homogeneity is a fairly heroic assumption. Belief differences may arise due to information differences or differing interpretations of information and have the potential to dramatically impact asset prices and trading dynamics. Several theoretical papers such as Shefrin (2001), Ziegler (2003), Basak (2005), Buraschi & Jiltsov (2006) and Li (2013) develop option pricing models to incorporate investor heterogeneous beliefs and show that belief differences affect option prices and thus explain the option-implied volatility smiles.

Friesen et al. (2012) empirically test the impact of investor heterogeneous beliefs on option prices by examining the cross-sectional relation between investor heterogeneous beliefs and the risk neutral skewness. They find stocks with greater belief differences have more negative risk neutral skews. The risk neutral skewness is measured by combining the prices of puts and calls. It is possible, the effect of heterogeneous beliefs on prices of puts and calls can be different. Feng et al. (2015) show differential relationships of puts and calls with stock returns. Therefore author examined the cross-sectional relationship between heterogeneous beliefs and option implied volatility smiles which allow me to measure put slope and call slope separately.

Using individual stock options traded on the Chicago Board Options Exchange (CBOE) from 2003 to 2005, author found that stocks with greater amount of open interest in out-of-the-money options, greater dispersion in financial analysts’ earnings forecasts and higher trading volume have more pronounced volatility smiles. The volatility smile is also more pronounced for small stocks, growth stocks (low earnings-to-price ratios) and value stocks (high book-to-market ratios). The latent factor for belief differences from factor analysis also shows strong correlations with smile slopes. My results confirm the findings of Friesen et al. (2012) that investor heterogeneous beliefs affect option values and further demonstrate the impact is same for puts and calls. The findings of this study also suggest that empirical studies of heterogeneous beliefs are robust to various different measures of option prices.

Literature Review and Hypothesis Development

There are various explanations for the volatility smile, which refers to the observed tendency of option-implied volatility to vary across strike prices. Some explanations relate to violations of the assumptions of the Black-Scholes model (e.g. violations of lognormally distributed returns or constant volatility). For instance, Hull (1993) points out that the volatility smile may be a consequence of empirical violations of the assumption of the normality of the log return. In addition, Bakshi et al. (2003) show that leptokurtic returns will cause the Black-Scholes model to misprice out-of-the-money (OTM) or in-the-money (ITM) options. Hull & White (1988) and Heston (1993) suggest that the volatility smile reflects stochastic volatility. Pena et al. (1999) show that transaction costs also affect the curvature of the volatility smile. Toft & Prucyk (1997) propose the leverage argument that more highly levered firms have steeper smiles. Other studies suggest that firm-specific factors are more important than the variation in systematic factors in explaining the smiles of individual stock options. For example, Dennis & Mayhew (2002) find the volatility smile of stock options is affected by liquidity and market risk measured by beta and size.

Another direction of research relates the volatility smile to market participants. Bollen & Whaley (2004) find net buying pressure determines the shape of the volatility smile, which they attribute to limits to arbitrage. Alternatively, several studies such as Shefrin (2001), Ziegler (2007), Buraschi & Jiltsov (2006) and Li (2013) relate the volatility smile to heterogeneous beliefs of investors. Friesen et al. (2012) examine the cross-sectional relation between heterogeneous beliefs and option prices using risk neutral skewness measure. They find stocks with greater investor belief heterogeneity have more negative risk neutral skews.

Different from the study of Friesen et al. (2012), researchers use volatility smile to examine the impact of heterogeneous beliefs on options. If heterogeneous beliefs affect the volatility smile, as the models in the previous section suggest, then greater belief differences will result in more pronounced volatility smiles. The determining characteristic of the volatility smile is that the implied volatility for out-of-the-money (OTM) individual stock options (both OTM puts and OTM calls) is greater than the implied volatility of at-the-money (ATM) options. When the implied volatility (vertical axis) is plotted against the strike price (horizontal axis), the put slope is therefore negative and the call slope is positive. When study refer to a more “pronounced smile”, author described absolute slope: “more pronounced” is defined as a more negative put slope and a more positive call slope.

To measure investor heterogeneous beliefs, author adopted the six proxy variables used in the paper of Friesen et al. (2012): firm size, earnings-to-price ratio, book-to-market ratio, dispersion in financial analysts’ earnings forecast, option open interest and stock trading volume. Hence my hypotheses are:

H1 Small stocks have more pronounced volatility smiles than large stocks. Equivalently, firm size should be positively related to the put slope (which is negative) and negatively related to the call slope (which is positive).

H2 Growth stocks have more pronounced volatility smiles than income stocks. Equivalently, the earnings-to-price ratio should be positively related to the put slope and negatively related to the call slope.

H3 Stocks with higher book-to-market ratios have more pronounced volatility smiles than stocks with lower book-to-market ratios. Equivalently, the book-to-market ratio should be negatively related to the put slope and positively related to the call slope.

H4 Stocks with a greater dispersion in financial analysts’ earnings forecasts have more pronounced volatility smiles than stocks with less dispersion in financial analysts’ earnings forecasts. Equivalently, the dispersion in financial analysts’ earnings forecasts should be negatively related to the put slope and positively related to the call slope.

H5 Stocks with more OTM option open interest have more pronounced volatility smiles. Equivalently, the put slope should be negatively related to OTM put option open interest while the call slope should be positively related to OTM call option open interest.

H6 Stocks with more trading volume have more pronounced volatility smiles. Equivalently, the stock trading volume should be negatively related to the put slope and positively related to the call slope.

Following the study of Friesen et al. (2012), research conducted factor analysis using the above six proxies for heterogeneous beliefs and obtain a latent factor for belief differences. Thus the last hypothesis is:

H7 The latent factor for heterogeneous beliefs should be negatively related to the put slope and positively related to the call slope.

Data and Methodology

This study uses a dataset on options traded on the Chicago Board Options Exchange (CBOE) from 2003 to 2005 provided by deltaneutral.com. The implied volatility is calculated using the mid-point of the bid and ask prices and inverting the Black-Scholes model using the bisection method. To be consistent with the existing literature, any option that violates basic arbitrage bounds is deleted. Options with zero open interest are also deleted. Since ITM options are less liquid than ATM or OTM options, the small volume of ITM options makes the quoted prices noisy. As optimistic investors demand OTM call options while pessimistic investors demand OTM put options, investor beliefs can be sufficiently reflected in OTM options. Therefore only OTM options are considered in this study. Only stocks which have both OTM puts and OTM calls are selected. Since most transactions are concentrated in the nearest expiration contracts, author uses only options with the shortest time to maturity. Following Whaley (1993), options with maturities less than seven days are eliminated. Therefore the sample is restricted to options with maturities between 7 and 30 days.

Unlike index options which exhibit monotonically decreasing implied volatilities with strike prices, implied volatilities of most stock options exhibit a “smile” shape. Followed Bollen & Whaley (2004) and consider separately the smile slopes of OTM puts and OTM calls. Using their moneyness, defined as the ratio of the strike price (X) to stock market price (S), options are categorized as follows: ATM options (0.95<=X/S<=1.05); OTM calls (X/S>1.05); OTM puts (X/S<0.95). The smile slope for OTM options is computed as the difference between the implied volatility of OTM options (IV_OTM) and the implied volatility of ATM options (IV_ATM) on the same underlying stock with the same expiration, divided by the difference between the moneyness of OTM options and the moneyness of ATM options.

To avoid differences in smile slopes driven by differences in stock price levels, moneyness is employed because it is comparable across stocks. If the implied volatility across the moneyness exhibits a “smile” shape, the put slope is negative and the call slope is positive. The robustness of results to alternative measures of smile slope is explained later.

Each day the implied volatility and the moneyness of options are averaged over all strike prices in each moneyness category, and then the put slope and the call slope are calculated. To test whether the volatility smile is related to heterogeneous beliefs at a cross-sectional level, author regress the smile slope on various proxies for heterogeneous beliefs described in Section I. The proxy variables are measured following the study of Friesen et al. (2012). Author included several control variables: bid-ask spread of the closing prices for OTM options as a proxy for transaction costs; time-to-expiration measured as the number of calendar days between the trade date and the expiration date; market uncertainty measured each month as the standard deviation of daily returns of value-weighted index including distributions; option volume used to proxy for liquidity and is summed over all options in each moneyness category. In addition, each firm’s market risk and idiosyncratic risk are also used as control variables. These are calculated each month by regressing daily stock returns on the daily returns of value-weighted index including distributions. Market risk is measured as beta and the idiosyncratic risk is measured as the standard deviation of residuals from the market model regression. Firm-specific variables are constructed each month using the data from the CRSP and the Compustat Industrial Quarterly File. For robustness checks, firm specific variables are also computed using daily stock prices rather than prices as of the last day of the previous month. The results based on daily stock prices are discussed in the section of robustness checks.

Empirical Results

Table 1 presents summary statistics for option-implied volatilities and smile slopes. The sample includes options on 865 stocks. The mean (median) implied volatility of OTM puts is 85% (73%) and the mean (median) implied volatility of OTM calls is 66% (57%). Both are higher than the mean (median) implied volatility of ATM options 46% (43%). The average put slope is -1.59, steeper than the average call slope 0.68. As argued in Buraschi & Jiltsov (2006), because the marginal utility is higher (lower) in bad (good) states of the world, the cost of an OTM put is higher than that of an OTM call, thus the implied volatility of an OTM put is higher than that of an OTM call.

Table 1 Summary Statistics on the Implied Volatility Smile
	Full Sample				Smile Sample (82%)				Skew Sample (18%)
	Obs	Mean	Median	Standard Deviation	Obs	Mean	Median	Standard Deviation	Obs	Mean	Median	Standard Deviation
IV of ATM Options	144627	0.46	0.43	0.18	117836	0.45	0.43	0.15	25574	0.48	0.45	0.20
IV of OTM Puts	144627	0.85	0.73	0.46	117836	0.87	0.75	0.46	25574	0.74	0.66	0.43
IV of OTM Calls	144627	0.66	0.57	0.38	117836	0.71	0.62	0.39	25574	0.45	0.42	0.16
PUT SLOPE	144627	-1.59	-1.37	1.20	117836	-1.72	-1.49	1.15	25574	-1.16	-0.97	0.99
CALL SLOPE	144627	0.68	0.56	0.93	117836	0.89	0.72	0.80	25574	-0.25	-0.18	0.72

This Table 1 presents descriptive statistics for option-implied volatilities and smile slopes. Sample includes options traded on CBOE for 865 stocks during the period from January 2003 to December 2005. The implied volatility is calculated using the mid-point of ask and bid prices, inverting the Black-Scholes model using the bisection method. Any option that violates the basic arbitrage bounds and has no open interest is excluded. Only stocks with both OTM puts and OTM calls with a maturity between 7 and 30 days are selected. Options are categorized based on the ratio of the strike price (X) to the current stock price (S): At-the-money options (0.95<=X/S<=1.05); Out-of-the-money calls (X/S>1.05); Out-of-the-money puts (X/S<0.95). Smile sample includes options with the implied volatility of OTM puts greater than that of ATM options and the implied volatility of OTM calls greater than that of ATM options. Skew samples are those options with the implied volatility of OTM puts greater than that of ATM options and the implied volatility of OTM calls smaller than that of ATM options. PUT (CALL) SLOPE is a measure of the implied volatility smile slope of OTM puts (calls), computed as the ratio of the difference of the implied volatility of OTM puts (calls) and ATM options to the difference of the moneyness of OTM puts (calls) and ATM options.

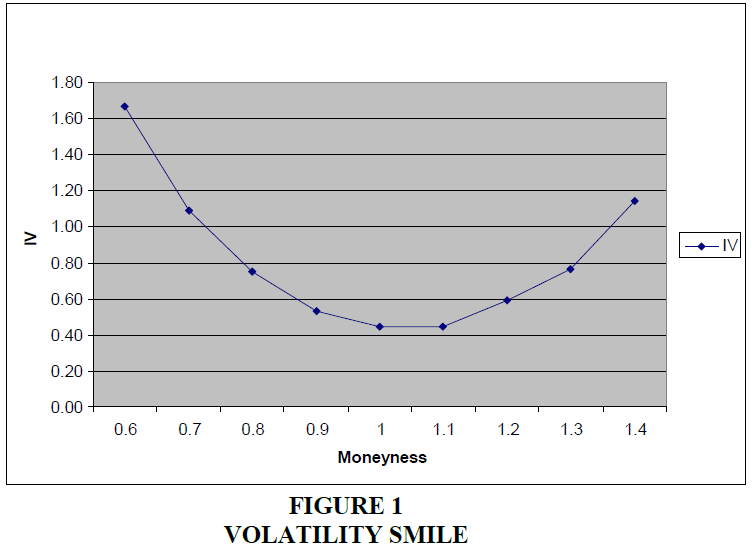
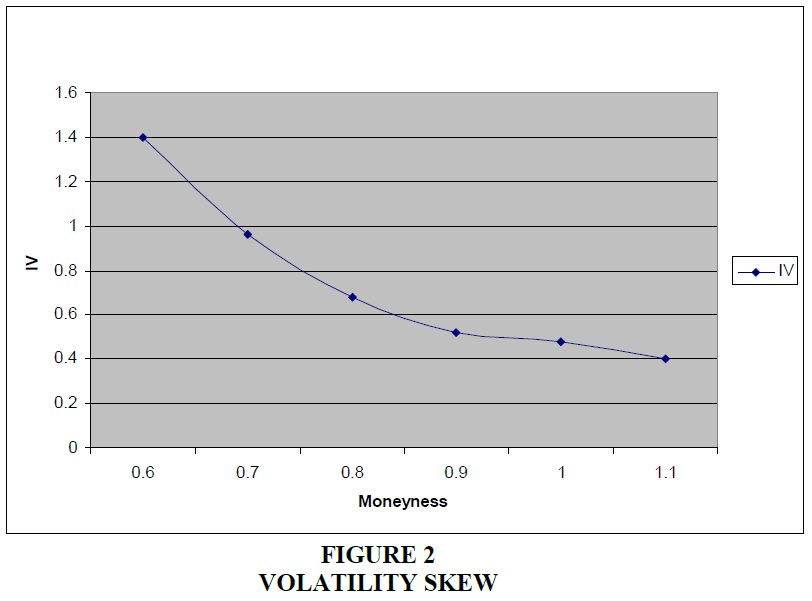
Consistent with the findings of Bollen and Whaley (2004), about 82% of the sample exhibit a “smile” shape. The average implied volatility of the smile sample (117,836 observations) is plotted across the moneyness in Figure 1. The put slope is negative (-1.72) and steeper than the call slope (0.89). About 18% of the sample (25,574 observations) exhibits monotonically decreasing implied volatilities with strike prices, which refered to as the volatility skew (Figure 2). The mean put slope and the mean call slope are negative: -1.16 and -0.25 respectively, but the put slope is much steeper than the call slope. A small number of observations in the sample exhibit shapes not characterized as a smile or a skew, and these observations are omitted from the analysis.

This figures 1 & 2 plots the mean implied volatility across moneyness for short-dated options (maturity between 7 and 30 days) on 865 stocks during the period of January 2003 to December 2005.

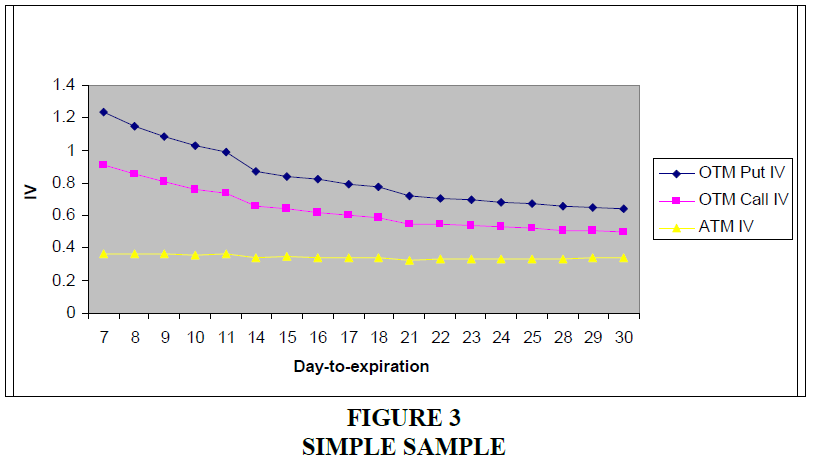
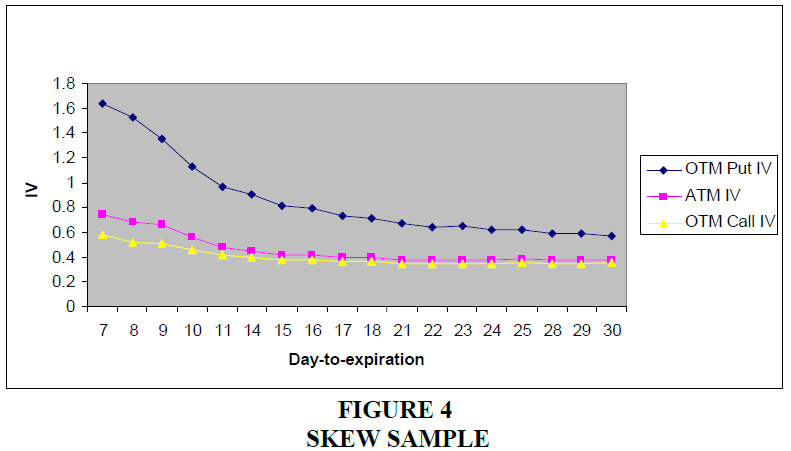
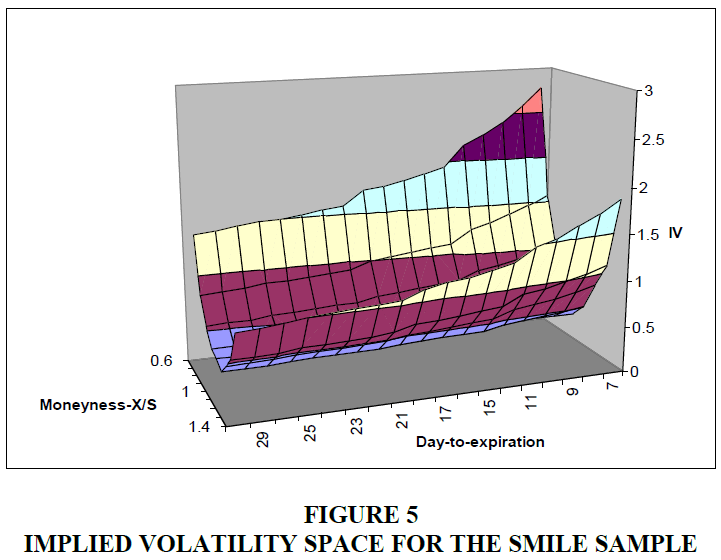
Figures 3 & 4 shows the term structure of the implied volatility the variation of the implied volatility with the maturity of the option. The implied volatilities of OTM puts and OTM calls increase as options become closer to expiration. The implied volatilities of short-dated ATM options in the smile sample are nearly constant across time-to-expiration as shown in Figure 3. The implied volatilities of short-dated ATM options in the skew sample increase slightly as options become closer to expiration as shown in Figure 4. Figure 5 illustrates the average implied volatility surface for the smile sample the variation of the implied volatility across moneyness and day-to-expiration. The smile becomes more pronounced when the option becomes closer to expiration.

This figure 3 & 4 plots the average implied volatility of options in each category with day-to-expiration. The sample contains options on 865 stocks over the period of January 2003 to December 2005.

This figure plots the implied volatility across moneyness and day-to-expiration for the smile sample. The time period is from January 2003 to December 2005.

Table 2 presents summary statistics for variables of the full sample that are used for hypothesis testing. The average daily open interest is about 4,780 contracts for OTM puts and about 5,860 contracts for OTM calls. The daily traded contracts are about 200 for OTM puts and 270 for OTM calls, consistent with the findings of Bollen and Whaley (2004) that more trading in stock options involves calls than puts. The mean (median) bid-ask spread for OTM puts is 16 cents (15 cents), slightly more than for OTM calls: 15 cents (13 cents).

Table 2 Summary Statistics
Variable	Mean	Median	Standard Deviation
OTM PUTS:
PUT SLOPE	-1.59	-1.37	1.20
OPEN INTEREST (in thousands)	4.78	0.50	19.23
OPTION VOLUME (in thousands)	0.20	0.00	1.27
SPREAD	0.16	0.15	0.35
OTM CALLS:
CALL SLOPE	0.68	0.56	0.93
OPEN INTEREST (in thousands)	5.86	0.63	26.56
OPTION VOLUME (in thousands)	0.27	0.00	1.54
SPREAD	0.15	0.13	0.24
OTHER  VARIABLES:
BETA	1.52	1.44	1.02
IDIOSYNCRATIC RISK (%)	2.25	1.97	1.23
MARKET VOLATILITY (%)	0.72	0.64	0.22
D/E	0.11	0.00	0.48
SIZE	21.24	21.00	1.36
E/P	0.04	0.03	0.03
BOOK-TO-MARKET	0.32	0.27	0.37
DISPERISON	0.14	0.05	0.38
STOCK VOLUME (in millions)	2.81	0.68	8.57

Most stocks in the sample are of medium and large capitalization because most small stocks do not have options or are not followed by financial analysts. The average firm size in the sample is about $1.68 billion. The average beta is 1.52 with the daily idiosyncratic risk of 2.25%. The average daily market volatility is 0.72%. The mean debt-to-equity ratio is 0.11 and a large number of firms in the sample have no long-term debt. The mean earnings-to-price ratio is 0.04, which is equivalent to a P/E ratio of 25. The mean (median) book-to-market ratio is 0.32 (0.27). The mean (median) dispersion in financial analysts’ earnings forecasts is 0.14 and the average daily stock trading volume is about 2.81 million shares.

This Table 2 presents summary statistics for variables that are used in subsequent regressions. Sample includes options traded on CBOE for 865 stocks during the period from January 2003 to December 2005. PUT (CALL) SLOPE is a measure of the implied volatility smile slope of OTM puts (calls), computed as the ratio of the difference of the implied volatility of OTM puts (calls) and ATM options to the difference of the moneyness of OTM puts (calls) and ATM options. OPEN INTEREST is the daily open interest on OTM options. OPTION VOLUME is the daily traded contracts on OTM options. SPREAD is the bid-ask spread on the daily closing OTM option prices. BETA is estimated by the market model for each month using daily data. IDIOSYNCRATIC RISK is the estimated standard deviation of daily stock returns using the market model for each month. MARKET VOLATILITY is the standard deviation of daily returns of value-weighted index including distributions for each month. D/E is the debt-to-equity ratio computed as the long term debt divided by the market capitalization as of the last day of previous month. SIZE is the natural logarithm of the market capitalization as of the last day of previous month. E/P is the earnings-to-price ratio as of the last day of previous month, computed as the quarterly earnings divided by the market price. BOOK-TO-MARKET is the book-to-market ratio computed as the book common equity value divided by the market capitalization as of the last day of previous month. DISPERSION is the dispersion of financial analysts' forecasts for quarter earnings, measured by the standard deviation of forecasts scaled by the absolute value of the mean forecast. STOCK VOLUME is the daily stock trading volume.

The bid-ask spread of OTM options is negatively related to the put slope and positively related to the call slope, suggesting options with high transaction costs have more pronounced smiles. This is consistent with the findings of Pena et al. (1999). Also the coefficient on the option volume is positive for the put slope and negative for the call slope, suggesting that illiquid options have more pronounced smiles than liquid options. The findings are consistent with previous studies that the volatility smile is affected by time-to-expiration, transaction costs and the liquidity of options.

Table 3 reports regression results in which the smile slope is regressed on the proxies for belief differences. Panel A presents results on the put slope and Panel B presents results on the call slope. For reference, column (1) includes only control variables. The put slope is positively related to day-to-expiration and the call slope is negatively related to day-to-expiration, indicating the smile becomes more pronounced as the expiration gets closer, consistent with the patterns shown in Figures 3 & 4 (recall, a more pronounced smile has a more negative put slope and a more positive call slope). The t-statistics for day-to-expiration are very large. To examine whether the difference in the smile slope is driven simply by day-to-expiration, author also run regressions for each day-to-expiration and results (discussed in the next section) are not qualitatively different.

Table 3 Volatility Smile Slope Regression
Panel A: PUT SLOPE
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
INTERCEPT	-3.168***	-4.391***	-3.240***	-3.142***	-3.162***	-3.127***	-3.154***	-5.533***
	(-80.42)	(-15.50)	(-84.34)	(-70.90)	(-80.20)	(-75.05)	(-75.62)	(-17.91)
EXPDAYS	0.092***	0.092***	0.092***	0.092***	0.092***	0.091***	0.092***	0.091***
	(147.02)	(147.17)	(147.23)	(157.23)	(147.03)	(148.48)	(147.25)	(157.50)
SPREAD	-0.798***	-0.772***	-0.803***	-0.784***	-0.798***	-0.811***	-0.806***	-0.767***
	(-2.79)	(-2.68)	(-2.80)	(-2.74)	(-2.79)	(-2.82)	(-2.80)	(-2.64)
OPTION VOLUME	0.007*	0.007***	0.006*	0.005	0.006*	0.035***	0.014***	0.028***
	(1.86)	(3.14)	(1.77)	(1.37)	(1.75)	(4.43)	(3.80)	(4.01)
BETA	0.000	0.002	0.007	0.000	0.000	0.000	0.000	0.013***
	(-0.05)	(0.39)	(1.50)	(0.05)	(0.08)	(0.00)	(-0.03)	(2.78)
IDIOSYNCRATIC RISK	0.467	2.505***	1.577***	0.598	0.624	0.065	0.242	4.728***
	(1.14)	(4.66)	(3.79)	(1.62)	(1.52)	(0.16)	(0.60)	(8.92)
MARKET VOLATILITY	4.981**	4.411*	7.983***	7.724***	4.952**	4.381*	5.602**	9.468***
	(2.04)	(1.78)	(3.22)	(3.40)	(2.03)	(1.81)	(2.24)	(3.99)
D/E	-0.073***	-0.062***	-0.056***	-0.010	-0.070***	-0.076***	-0.075***	-0.012
	(-6.16)	(-5.46)	(-4.49)	(-0.89)	(-6.10)	(-6.34)	(-6.26)	(-1.20)
SIZE		0.055***						0.329***
		(4.89)						(17.55)
E/P			1.027***					0.986***
			(12.23)					(13.43)
BOOK-TO-MARKET				-0.177**				-0.130**
				(-2.28)				(-2.06)
DISPERISON					-0.070***			-0.027**
					(-4.49)			(-2.27)
OPEN INTEREST						-0.005***		-0.006***
						(-11.04)		(-16.45)
STOCK VOLUME							-0.005***	-0.009***
							(-4.67)	(-16.61)
Adjusted R^2 (%)	35.57	35.89	36.17	35.65	35.62	36.1	35.67	37.55
Panel B: CALL SLOPE
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
INTERCEPT	1.987***	2.961***	2.009***	1.939	1.981***	1.97***	1.969***	3.607***
	(95.02)	(24.97)	(96.28)	(61.87)	(94.83)	(92.24)	(91.45)	(21.28)
EXPDAYS	-0.063***	-0.062***	-0.063***	-0.063***	-0.062***	-0.062***	-0.062***	-0.062***
	(-130.81)	(-131.23)	(-130.61)	(-138.72)	(-130.80)	(-130.69)	(-130.89)	(-138.61)
SPREAD	0.901***	0.860***	0.904***	0.897***	0.902***	0.913***	0.919***	0.869***
	(8.11)	(7.80)	(8.11)	(8.25)	(8.11)	(8.09)	(8.06)	(7.95)
OPTION VOLUME	-0.006***	0.004***	-0.006***	-0.004**	-0.006***	-0.017***	-0.017***	-0.015***
	(-3.99)	(2.91)	(-3.90)	(-1.99)	(-3.79)	(-8.09)	(-10.27)	(-8.74)
BETA	-0.022***	-0.024***	-0.024***	-0.021***	-0.022***	-0.022***	-0.022***	-0.026***
	(-6.78)	(-7.30)	(-7.39)	(-7.22)	(-6.97)	(-8.48)	(-6.84)	(-8.86)
IDIOSYNCRATIC RISK	-3.186***	-4.838***	-3.567***	-3.115***	-3.329***	-2.997***	-2.856***	-5.622***
	(-11.07)	(-14.48)	(-12.38)	(-12.03)	(-11.52)	(-10.51)	(-10.01)	(-15.70)
MARKET VOLATILITY	-28.490***	-27.951***	-29.354***	-29.563***	-28.462***	-28.610***	-29.362***	-30.458***
	(-13.53)	(-13.24)	(-13.83)	(-14.98)	(-13.52)	(-13.59)	(-13.85)	(-15.36)
D/E	0.037***	0.029***	0.033***	-0.025***	0.035***	0.039***	0.040***	-0.023***
	(4.77)	(3.96)	(4.16)	(-2.76)	(4.66)	(4.92)	(4.96)	(-2.73)
SIZE		-0.044***						-0.076***
		(-8.87)						(-11.30)
E/P			-0.324***					-0.218***
			(-8.38)					(-6.43)
BOOK-TO-MARKET				0.193**				0.158**
				(2.27)				(2.16)
DISPERISON					0.063***			0.042***
					(6.93)			(5.64)
OPEN INTEREST						0.002***		0.002***
						(7.55)		(7.54)
STOCK VOLUME							0.006***	0.010***
							(13.48)	(18.92)
Adjusted R^2 (%)	29.09	29.41	29.22	29.51	29.06	29.32	29.32	30.68

Table 4 Quintile Smile Slope
Panel A: Stocks Sorted on Firm Size											Panel B: Stocks Sorted on the Earnings-to-price Ratio
SIZE		PUT SLOPE			CALL SLOPE						E/P	PUT SLOPE		CALL SLOPE
Quintiles		Mean	Median		Mean					Median	Quintiles	Mean	Median	Mean	Median
1(Small)		-2.02	-1.83		0.98					0.90	1(Small)	-2.11	-1.94	0.91	0.85
2		-1.77	-1.60		0.81					0.72	2	-1.94	-1.77	0.83	0.76
3		-1.70	-1.53		0.73					0.65	3	-1.91	-1.73	0.79	0.72
4		-1.63	-1.48		0.66					0.60	4	-1.91	-1.68	0.78	0.68
5(Large)		-1.52	-1.45		0.62					0.59	5(Large)	-1.82	-1.60	0.78	0.66
Q5-Q1		0.50	0.38		-0.24					-0.31	Q5-Q1	0.29	0.34	-0.13	-0.19
		(20.78)	(16.77)		(-21.47)					(-21.88)		(5.02)	(5.87)	(-3.41)	(-5.76)
Panel C: Stocks Sorted on the Book-to-market Ratio											Panel D: Stocks Sorted on the Dispersion in Analysts’ Forecasts
BOOK-TO-MARKET		PUT SLOPE			CALL SLOPE						DISPERSION	PUT SLOPE		CALL SLOPE
Quintiles		Mean	Median		Mean					Median	Quintiles	Mean	Median	Mean	Median
1(Small)		-1.60	-1.47		0.58					0.51	1(Small)	-1.68	-1.51	0.71	0.60
2		-1.63	-1.48		0.66					0.59	2	-1.59	-1.46	0.70	0.62
3		-1.66	-1.51		0.73					0.66	3	-1.68	-1.51	0.74	0.64
4		-1.78	-1.58		0.84					0.75	4	-1.78	-1.59	0.80	0.72
5(Large)		-1.96	-1.76		1.00					0.90	5(Large)	-1.90	-1.70	0.86	0.77
Q5-Q1		-0.36	-0.29		0.42					0.39	Q5-Q1	-0.22	-0.19	0.15	0.17
		(-13.99)	(-13.80)		(22.68)					(24.54)		(-8.38)	(-8.98)	(7.72)	(11.19)
Panel E: Stocks Sorted on Open Interest											Panel F: Stocks Sorted on Stock Volume
OPEN INTEREST	PUT SLOPE						CALL SLOPE				STOCK VOLUME	PUT SLOPE		CALL SLOPE
Quintiles	Mean			Median			Mean		Median		Quintiles	Mean	Median	Mean	Median
1(Small)	-1.92			-1.71			0.99		0.91		1(Small)	-2.03	-1.82	0.98	0.89
2	-1.81			-1.59			0.90		0.81		2	-1.84	-1.67	0.86	0.78
3	-1.70			-1.55			0.73		0.68		3	-1.67	-1.52	0.72	0.68
4	-1.63			-1.49			0.62		0.59		4	-1.56	-1.44	0.61	0.59
5(Large)	-1.58			-1.50			0.56		0.54		5(Large)	-1.54	-1.47	0.63	0.61
Q5-Q1	0.34			0.21			-0.43		-0.37		Q5-Q1	0.49	0.34	-0.35	-0.28
	(13.60)			(7.90)			(-23.70)		(-23.69)			(17.96)	(14.03)	(-17.17)	(-16.14)
Panel G: Stocks Sorted on the Residuals of Open Interest on Firm Size											Panel H: Stocks Sorted on the Residuals of  Stock Volume on Firm  Size
OPEN INTEREST	PUT SLOPE					CALL SLOPE					STOCK VOLUME	PUT SLOPE		CALL SLOPE
Quintiles	Mean			Median		Mean		Median			Quintiles	Mean	Median	Mean	Median
1(Small)	-1.54			-1.41		0.58		0.51			1(Small)	-1.56	-1.45	0.61	0.55
2	-1.65			-1.49		0.71		0.62			2	-1.64	-1.48	0.69	0.62
3	-1.72			-1.53		0.74		0.66			3	-1.71	-1.54	0.75	0.66
4	-1.81			-1.64		0.85		0.75			4	-1.79	-1.62	0.80	0.72
5(Large)	-1.92			-1.72		0.92		0.82			5(Large)	-1.95	-1.74	0.95	0.86
Q5-Q1	-0.38			-0.31		0.34		0.31			Q5-Q1	-0.39	-0.29	0.34	0.31
	(-15.14)			(-17.16)		(18.47)		(24.61)				(-15.22)	(-15.04)	(17.87)	(21.68)

This Table 3 presents regression results of the smile slope. The sample includes 144,627 daily observations during the period from January 2003 to December 2005. EXPDAYS is the number of calendar days between the trade date and the expiration date. Robust Newey-West t-statistics are reported in parentheses under the parameter estimates.

Contrary to the results of Dennis and Mayhew (2002), column (1) indicates no significant relation between the put slope and beta but a significant negative relation between the call slope and beta. The smile is more pronounced during periods of low market volatility. The put slope is unrelated to the idiosyncratic risk of stocks while the call slope is negatively related to the idiosyncratic risk. This suggests that OTM calls have higher implied volatilities relative to ATM options when firm’s idiosyncratic risk is low, consistent with the results of Dennis and Mayhew (2002). Author also find highly levered firms have steeper call slopes, which is inconsistent with the leverage argument.

To test my first hypothesis, firm size is added into the regression. Column (2) shows that the coefficient on firm size is significantly positive (0.055) for the put slope and significantly negative (-0.044) for the call slope, supporting the hypothesis that small firms have more pronounced smiles than large firms. Column (3) shows that the earnings-to-price ratio is significantly positively (1.027) related to the put slope and significantly negatively (-0.324) related to the call slope, indicating that growth stocks have more pronounced smiles than income stocks and thus supporting hypothesis 2. Similarly, column (4) shows that estimated coefficients on the book-to-market ratio have their predicted signs: negative (-0.177) for the put slope and positive (0.193) for the call slope, supporting hypothesis 3 that stocks with high book-to-market ratios have more pronounced volatility smiles.

Column (5) in Table 3 shows that the dispersion in financial analysts’ earnings forecasts is negatively related to the put slope and positively related to the call slope, supporting hypothesis 4 that stocks with higher dispersion in financial analysts’ earnings forecasts have more pronounced volatility smiles. Column (6) and (7) show that coefficients on open interest and stock trading volume have their predicted signs: negative for the put slope and positive for the call slope. Stocks with more OTM option open interest or more trading volume on stocks have more pronounced volatility smiles, supporting hypotheses 5 and 6. The relation between the smile slope and open interest also supports the trading pressure argument of Bollen and Whaley (2004) that option prices are affected by the demand in options.

Table 4 presents mean and median put slopes and call slopes for five stock quintiles. Each month stocks are assigned into five quintiles based on a particular proxy for heterogeneous beliefs: size, earnings-to-price ratio, book-to-market ratio, dispersion in financial analysts’ earnings forecasts, open interest and stock trading volume. Table 4 Panel A shows that small capitalization quintile have more pronounced smiles, supporting the first hypothesis. Quintiles of the earnings-to-price ratio exhibit similar patterns in Panel B. Growth stocks have more pronounced smiles than income stocks. Panel C and D show that absolute values of the put slope and the call slope are monotonically increasing when moving from the lowest quintile to the highest quintile of the book-to-market ratio and the dispersion in analysts’ earnings forecasts respectively, supporting the third and fourth hypotheses. All the slope differentials between the highest and the lowest quintile are statistically significant.

This Table 4 presents mean and median smile slopes of stocks sorted on firm characteristics. Each month stocks are assigned into five quintiles based on the variable of interest. PUT (CALL) SLOPE is computed as the ratio of the difference of the implied volatility of OTM puts (calls) and ATM options to the difference of the moneyness of OTM puts (calls) and ATM options based on daily data, and then averaged across each month. SIZE is the natural logarithm of the market capitalization as of the last day of previous month. E/P is the earnings-to-price ratio as of the last day of previous month, computed as the quarterly earnings divided by the market price. BOOK-TO-MARKET is the book-to-market ratio computed as the book common equity value divided by the market capitalization as of the last day of previous month. DISPERSION is the dispersion of financial analysts' forecasts for quarter earnings, measured by the standard deviation of forecasts scaled by the absolute value of the mean forecast. OPEN INTEREST is the daily open interest on OTM put (or call) options averaged across each month. STOCK VOLUME is the daily stock trading volume averaged across each month. In Panel G and Panel H, open interest and stock volume are first regressed on firm size and then residuals are obtained. Each month stocks are sorted on the residuals of open interest and residuals of stock volume into five quintiles respectively. The mean and median of PUT SLOPE and CALL SLOPE on all stocks in each quintile are reported. T-statistics for testing the difference in the means equal to zero and z-statistics for testing the difference in the medians equal to zero are reported in parentheses.

Following Friesen et al. (2012), factor analysis is applied to the Spearman correlation matrix of six proxies for heterogeneous beliefs, as shown in Table 5. The factor analysis produces two factors. Results for maximum likelihood method and the principal factor methods are presented in Table 6 Panel A and Panel B respectively. Two factors are extracted using either method. The first factor measures firm size while the second factor is associated with belief differences. Then latent factor of heterogeneous beliefs is calculated as a linear combination of proxies using factor score coefficients.

Table 5 Spearman Correlation Coefficients
	DISPERSION	STOCK VOLUME	SIZE	E/P	BOOK-TO-MARKET
STOCK VOLUME	-0.11
SIZE	-0.27	0.70
E/P	-0.33	-0.05	-0.10
BOOK-TO-MARKET	0.13	-0.24	-0.27	0.16
OPEN INTEREST	-0.03	0.72	0.50	-0.11	-0.26

Table 6 Factor Analysis
Panel A: Maximum Likelihood Method
	Initial Factor Pattern		Rotated Factor Pattern		Factor Score
	Factor1	Factor2	Factor1	Factor2	Factor1	Factor2
DISPERSION	-0.15	0.62	-0.12	0.62	-0.00	0.45
STOCK VOLUME	0.94	0.04	0.94	0.00	0.71	0.13
SIZE	0.75	-0.25	0.74	-0.29	0.15	-0.30
E/P	-0.04	-0.53	-0.06	-0.53	-0.02	-0.33
BOOK-TO-MARKET	-0.28	0.00	-0.28	0.02	-0.03	0.00
OPEN INTEREST	0.75	0.16	0.76	0.12	0.16	0.16
Common Variance Explained	71%	29%	70%	30%
Panel B: Principal Factor Method
	Initial Factor Pattern		Rotated Factor Pattern		Factor Score
	Factor1	Factor2	Factor1	Factor2	Factor1	Factor2
DISPERSION	-0.19	-0.49	-0.12	-0.51	-0.07	-0.33
STOCK VOLUME	0.86	-0.07	0.86	-0.05	0.50	-0.05
SIZE	0.75	0.20	0.72	0.31	0.22	0.32
E/P	-0.02	0.52	-0.09	0.51	-0.05	0.34
BOOK-TO-MARKET	-0.34	0.08	-0.34	0.03	-0.09	0.04
OPEN INTEREST	0.74	-0.20	0.76	-0.07	0.26	-0.18
Common Variance Explained	75%	25%	75%	25%

This Table 5 presents Spearman correlation coefficients for seven proxies for heterogeneous beliefs that are used in subsequent factor analysis. The sample includes 865 firms during the period from January 2003 to December 2005. Each proxy variable is measured at monthly frequency. DISPERSION is the dispersion in financial analysts’ earnings forecasts, measured as the standard deviation of forecasts for quarterly earnings scaled by the absolute value of the mean earnings forecast. STOCK VOLUME is the average daily stock trading volume in millions. SIZE is the nature logarithm of the market capitalization as of the last day of previous month. E/P is the earnings-to-price ratio as of the last day of previous month, computed as the quarterly earnings divided by the market price. BOOK-TO-MARKET is the book-to-market ratio computed as the book common equity value divided by the market capitalization as of the last day of previous month. OPEN INTEREST is daily total open interests on both OTM puts and OTM calls averaged across each month.

This Table 6 presents results of the factor analysis. Panel A presents results using maximum likelihood method and Panel B presents results using principal factoring method. The factor analysis is based on the Spearman correlation between seven proxy variables. The prior communality estimate for each variable is set to its squared multiple correlation of each variable with all remaining variables. Varimax orthogonal rotation method is employed to rotate factors.

Table 7 reports of regression results of put slope and call slope on the latent factor. The latent factor is negatively related to the put slope and positively related to the call slope, supporting the hypothesis that stocks with greater belief differences have more pronounced smiles. The absolute value of t-statistics for the coefficients of the latent factor is relatively large compared to that of proxy variables as shown in Table 3. The latent factor has a stronger relationship with the volatility smile compared to proxy variables. The adjusted R-square is generally slightly higher relative to the adjusted R-square of regressions on proxy variables. These results support the argument that the latent factor is a less noisy measure of heterogeneous beliefs.

Table 7 Smile Slope Regressions Using the Latent Factor for Heterogeneous Beliefs
	Maximum Likelihood Method		Principal Factor Method
	PUT SLOPE	CALL SLOPE	PUT SLOPE	CALL SLOPE
INTERCEPT	-3.275***	2.038***	-3.277***	2.036***
	(-86.49)	(121.31)	(-85.28)	(120.18)
EXPDAYS	0.091***	-0.063***	0.091***	-0.063***
	(197.33)	(-153.66)	(197.16)	(-153.54)
SPREAD	-0.779***	0.893***	-0.777***	0.891***
	(-2.76)	(8.40)	(-2.76)	(8.39)
OPTION VOLUME	0.007**	-0.007***	0.005	-0.005***
	(2.06)	(-4.75)	(1.56)	(-3.87)
BETA	0.010***	-0.027***	0.010***	-0.027***
	(2.97)	(-13.20)	(3.01)	(-13.08)
IDIOSYNCRATIC RISK	2.951***	-4.55***	3.044	-4.527***
	(11.66)	(-25.29)	(12.06)	(-25.21)
MARKET VOLATILITY	7.493**	-28.489***	7.401**	-28.391***
	(4.19)	(-19.46)	(4.15)	(-19.40)
D/E	-0.06***	0.034***	-0.063***	0.036***
	(-9.59)	(6.31)	(-9.86)	(6.71)
Latent Factor for Heterogeneous  Beliefs	-0.189***	0.111***	-0.212***	0.118***
	(-26.00)	(25.18)	(-24.08)	(23.26)
R^2 (%)	36.23	29.53	36.20	29.47

This Table 7 presents regression results of the put slope and the call slope on latent factors estimated from the factor analysis. Robust Newey-West t-statistics are reported in parentheses under the parameter estimates. The sample includes 144, 627 daily observations during the period from January 2003 to December 2005.

In addition, each month author used the estimated latent factor to sort stocks into five quintile portfolios based on the degree of belief differences. The mean and median put slope and call slope are reported in Table 8. Stocks with greater magnitude of the latent factor for heterogeneous beliefs have more negative put slopes and more positive call slopes, supporting the argument that stocks with greater belief heterogeneity have more pronounced volatility smiles. The differential slopes between the highest and lowest belief heterogeneity quintiles are significantly different from zero.

Table 8 Smile Slope of Stocks Sorted on the Latent Factor for Heterogeneous Beliefs
				Maximum Likelihood Method					Principal Factor Method
				PUT SLOPE		CALL SLOPE			PUT SLOPE		CALL SLOPE
INTERCEPT				-3.275***		2.038***			-3.277***		2.036***
				(-86.49)		(121.31)			(-85.28)		(120.18)
EXPDAYS				0.091***		-0.063***			0.091***		-0.063***
				(197.33)		(-153.66)			(197.16)		(-153.54)
SPREAD				-0.779***		0.893***			-0.777***		0.891***
				(-2.76)		(8.40)			(-2.76)		(8.39)
OPTION VOLUME				0.007**		-0.007***			0.005		-0.005***
				(2.06)		(-4.75)			(1.56)		(-3.87)
BETA				0.010***		-0.027***			0.010***		-0.027***
				(2.97)		(-13.20)			(3.01)		(-13.08)
IDIOSYNCRATIC RISK				2.951***		-4.55***			3.044		-4.527***
				(11.66)		(-25.29)			(12.06)		(-25.21)
MARKET VOLATILITY				7.493**		-28.489***			7.401**		-28.391***
				(4.19)		(-19.46)			(4.15)		(-19.40)
D/E				-0.06***		0.034***			-0.063***		0.036***
				(-9.59)		(6.31)			(-9.86)		(6.71)
Latent Factor for Heterogeneous  Beliefs				-0.189***		0.111***			-0.212***		0.118***
				(-26.00)		(25.18)			(-24.08)		(23.26)
R^2 (%)				36.23		29.53			36.20		29.47
Panel A: Maximum Likelihood Method							Panel B: Principal Factor Method
	PUT SLOPE		CALL SLOPE					PUT SLOPE				CALL SLOPE
Quintiles	Mean	Median	Mean		Median		Quintiles	Mean		Median		Mean	Median
1(Small)	-1.51	-1.42	0.59		0.54		1(Small)	-1.49		-1.42		0.60	0.55
2	-1.64	-1.50	0.71		0.61		2	-1.67		-1.52		0.72	0.63
3	-1.69	-1.51	0.77		0.67		3	-1.67		-1.50		0.76	0.66
4	-1.80	-1.63	0.84		0.74		4	-1.80		-1.63		0.83	0.74
5(Large)	-2.00	-1.81	0.90		0.84		5(Large)	-2.01		-1.81		0.90	0.82
Q5-Q1	-0.49	-0.40	0.31		0.30		Q5-Q1	-0.52		-0.39		0.30	0.27
	(-19.09)	(-19.79)	(16.55)		(21.42)			(-21.74)		(-19.62)		(17.62)	(20.02)

Robustness Checks

To investigate the robustness of the results presented in the previous section, several dimensions are examined, such as alternative measures of the volatility smile, separating samples by day-to-expiration, alternative measures of firm-specific variables and examining results by years.

To investigate the robustness of the results presented in the previous section, several dimensions are examined, such as alternative measures of the volatility smile, separating samples by day-to-expiration, alternative measures of firm-specific variables and examining results by years.

First, different measures of the volatility smile are used. Following Toft & Prucyk (1997), the smile slope is scaled by the implied volatility of ATM options. Dennis & Mayhew (2002) argue that this measure is a complex since it impounds information in both the implied volatility level and the smile slope. Using this alternative measure would be hard to distinguish the effects on the slope from the level. Buraschi & Jiltsov (2006) show that both the volatility smile and the volatility level are greater when investor have greater belief differences. Consistent with the prediction of Buraschi & Jiltsov (2006), this study finds the implied volatility levels of ATM options are higher for stocks with greater belief differences. But the results for the smile slope scaled by the implied volatility of ATM options do not change the conclusions presented in the previous section.

Alternatively, similar to Buraschi & Jiltsov (2006), the smile slope is measured as the difference of the implied volatility of OTM and ATM options, without dividing the difference of moneyness. The results on this alternative measure are not qualitatively different from results presented in the previous section. However R-squares of multivariate regressions based on the above two alternative measures of the volatility smile are smaller.

Because smile slopes become more pronounced as options become close to expiration, researcher run regressions of the smile slope by day-to-expiration. Regression results (will be provided at request) are consistent for each day-to-expiration with some exceptions that some coefficients on firm size and the dispersion in analysts’ earnings forecasts are insignificantly different from zero. The coefficients on the control variables (not reported here) are also consistent with results presented in Table 3.

Alternatively author construct firm size, debt-to-equity, earnings-to-price and book-to-market ratios using daily stock prices rather than prices of the last day of the previous month. The study used these daily measures in the regressions of the put and call slope, as shown in Table 3. The signs and significances of these variables remain unchanged.

Last, the study examines the results by year. Due to the availability of data, author did not fully replicating the study period of Friesen et al. (2012), which is from 2003 to 2006. So author examined the sample year by year and find the results consistent over years.

Conclusion

Friesen et al. (2012) among others show that belief differences can affect option prices. Optimistic investors drive up the prices of out-of-the-money calls while pessimistic investors drive up the prices of out-of-the-money puts. The result is that the implied volatility of out-of-the-money options is greater than the implied volatility of at-the-money options. Hence belief differences may be reflected in the option-implied volatility smile the variation of the implied volatility with strike prices.

This paper finds that stocks with greater belief heterogeneity have more pronounced volatility smiles. Small stocks, stocks with low earnings-to-price ratios and stocks with high book-to-market ratios have more pronounced smiles than large stocks, stocks with high earnings-to-price ratios and stocks with low book-to-market ratios, respectively. Also the volatility smile is correlated with the dispersion in financial analysts’ earnings forecasts, out-of-the-money option open interest and stock trading volume, which are widely used proxies for heterogeneous beliefs in literature. These results support the idea that the volatility smile is related to belief differences.

This study provides evidence that the impact of heterogeneous beliefs on options is significant and not subject to particular specifications of valuation. The findings of this study provide insight on the option valuation and valuable guidance for investors. As argued in Qin (2017) that heterogeneous beliefs improve the allocation efficiency of option markets, speculators in option investments can construct portfolios based on heterogeneous beliefs. Even though the time period under this study is short, recent study of Feng et al. (2018) found similar relation between volatility smile and heterogeneous beliefs for a long and extended time period, which proved the robustness of the results over time. Therefore, this study not only contributes to the literature of heterogeneous beliefs and option valuation, but also help practitioners and regulators understand the role of the investor divergent opinions on the options thus assist them in make better investment and regulating decisions.

References

1. Basak, S. (2005). Asset pricing with heterogeneous beliefs. Journal of Banking and Finance, 28(11),2849-2881.
2. Bakshi, G., Kapadia, N., & Madan, D. (2003). Stock return characteristics, skewness laws, and the differential pricing of individual equity options. Review of Financial Studies, 16, 101-143.
3. Bollen, N.P.B., & Whaley, R.E. (2004). Does net buying pressure affect the shape of implied volatility functions? Journal of Finance, 59(2), 711-753.
4. Buraschi, A., & Jiltsov, A. (2006). Model uncertainty and option markets with heterogeneous beliefs. Journal of Finance, 61(6), 2841-2897.
5. Dennis, P., & Mayhew, S. (2002). Risk-neutral skewness: Evidence from stock options. Journal of Financial and Quantitative Analysis, 37, 471-493.
6. Feng, S., Friesen, G.C., & Zhang, Y. (2015). The relationship between the option-implied volatility smile, stock returns and heterogeneous beliefs. International Review of Financial Analysis, 41, 62-73.
7. Feng, S., Pu, X., & Zhang, Y. (2018). An empirical examination of the relation between the option-implied volatility smile and heterogeneous beliefs. The Journal of Derivatives, 25(4), 36-47
8. Friesen, G.C., Zhang, Y., & Zorn, T.S. (2012). Heterogeneous beliefs and risk-neutral skewness. Journal of Financial and Quantitative Analysis, 47(4), 851-8722.
9. Heston, S.L. (1993). A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies, 6(2), 327-343.
10. Hull, J.C., & White, A. (1988). An analysis of the bias in option pricing caused by a stochastic volatility. Advances in Futures and Options Research, 3, 29-61.
11. Hull, J.C. (1993). Options, Futures, and Other Derivative Securities. Englewood Cliffs, NJ: Prentice Hall
12. Li, T. (2013). Heterogeneous beliefs, option prices, and volatility smiles . Management Science, 59(10), 2392-2412.
13. Pena, I., Rubio, G., & Serna, G. (1999). Why do I smile? On the determinants of the implied volatility function. Journal of Banking and Finance, 23(8), 1151-1179.
14. Qin, Z. (2017). Speculations in option markets enhance allocation efficiency with heterogeneous beliefs and learning. Journal of Banking and Finance, 37(12), 4675-4694.
15. Shefrin, H. (2001). On kernels and sentiment. Working Paper, Santa Clara University.
16. Toft, K.B., & B. Prucyk (1997). Options on leveraged equity: Theory and empirical tests. Journal of Finance, 53(3), 1151-1180.
17. Whaley, R.E. (1993). Derivatives on market volatility: Hedging tools long overdue. Journal of Derivatives, 1, 71-84.
18. Ziegler, A. (2003). Incomplete information and heterogeneous beliefs in continuous-time finance. New York, NY: Springer-Verlag New York, LLC
19. Ziegler, A. (2007). Why does implied risk aversion smile? Review of Financial Studies, 20(3), 859-904