Keywords

Multi-armed bandit model; Simulation; Initial belief; Exploration.

Introduction

An organization facing a set of alternatives often needs to make choices under uncertainty. In new product development, research and development, and marketing, the organization selects the optimal alternative in each period and receives a reward. For example, in online banner advertising, a manager must select one banner to expose in a specific period out of a wide variety of candidates (Urban et al., 2014). Customers may or may not click the exposed banner with uncertainty. The manager will receive a reward if the banner is clicked and receives no reward if not. The manager repeats this process during a given period and must select an appropriate banner in each period to maximize the cumulative rewards. Known as reinforcement learning, an environment (customers) responds (click or no click) to the manager’s action (selecting a banner), and the manager must identify an optimal strategy to expose banners based on the results of the interactions with the customers (Sutton & Barto, 1998). The manager obtains knowledge about the estimated click-through rates of banners based on the interaction to maximize the reward; that knowledge is updated as the selection results accumulate. This type of problem is a typical example of the multi-armed bandit model widely used in the management literature (Denrell & March, 2001; March, 2010). In this paper, we investigate the mechanism of the initial belief effect in the multi-armed bandit model.

A manager can maximize cumulative rewards by earning rewards and searching for more knowledge, leading to an exploration - exploitation tradeoff. Exploitation exploits the currently superior alternative for a guaranteed reward, whereas exploration seeks new knowledge by searching for potentially superior alternatives (Luger et al., 2018). Neither extreme exploration nor exploitation is optimal - an optimal strategy balances exploration and exploitation (March, 1991).

Therefore, organizations must balance exploration by seeking new knowledge from a potentially superior alternative and exploitation of a current alternative with superior value (Levinthal & March, 1993).

There has been extensive research on methods to identify optimal or near-optimal solutions to learning problems (Bubeck & Cesa-Bianchi, 2012). Gittins & Jones (1974) identified an optimal strategy under special conditions. However, their method is computationally intensive and intractable in most cases (Gans et al., 2007). Therefore, a wide range of methodologies, including ε-greedy, upper confidence bound, and greedy bandit, were developed to efficiently solve the multi-armed bandit problem (Sutton & Barto, 1998).

One interesting, effective method is to change initial belief about the success probabilities of alternatives (Sutton & Barto, 1998). Any method to solve the multi-armed bandit model must set an initial estimation, called initial belief, of the success probabilities of alternatives (e.g., probability of clicking each banner in the above online banner advertising example). In most research, initial belief is set to the average success probability of alternatives. However, initial belief does not have to match that average, and deviation of initial belief from the average might improve performance (Sutton & Barto, 1998). There has been research using this effect of the change in initial belief (Kaelbling et al., 1996; Moore & Atkenson, 1993; Tadepalli & Ok, 1998), but the detailed mechanism of the initial belief effect has not been explained sufficiently. Therefore, this study aims to reveal that mechanism using simulation experiments.

Model

We use the multi-armed bandit model (Robbins, 1952) to examine the impact of initial belief on the optimal exploration level in reinforcement learning. The multi-armed bandit model is widely used to analyze the exploration - exploitation tradeoff problem (March, 2010; Posen & Levinthal, 2012; Shahrokhi Tehrani & Ching, 2019). In the multi-armed bandit model, a decision-maker faces a set of alternatives, each yielding random rewards from a different probability distribution unknown to the decision-maker. One alternative must be chosen in each period. The decision-maker must identify valuable alternatives to maximize the overall rewards, possible only by gathering information from observing the resulting rewards of selections. In each period, the decision-maker faces the dilemma of exploration - exploitation. If the decision-maker exploits the current optimal alternative, the expected reward increases, but the opportunity to extend knowledge about less- or not-selected alternatives is lost. The decision-maker must explore less-examined alternatives but forgo the currently believed optimal alternative to increase knowledge about potentially superior alternatives.

In each period, the decision-maker receives a random reward for selecting an alternative: 1 if the selection is successful and 0 if not. The success probability of an alternative follows a Bernoulli distribution with a success parameter randomly drawn from a probability distribution called a payoff distribution. The decision-maker must estimate and update the true success probabilities of alternatives using trial-and-error. The estimated success probability, called belief, of alternative i at time t is denoted by Consistent wtih March (1996), when alternative i is selected at time t, the belief is updated as where the reward is 1 if the selection is successful and 0 otherwise, and is the number of selecting i until time t.

The degree of exploiting an alternative with current high belief or exploring an alternative with low belief is determined by the level of exploration. The decision-maker must determine the level strategically to maximize the total rewards. We use the softmax selection rule to implement the exploration level (Luce, 1959). The probability of choosing alternative i is exp where τ is the exploration level. When τ is near zero, the strategy is extreme exploitation and the alternative with the highest belief will be selected. When τ is larger than zero, an alternative is selected probabilistically. The probability of selecting a low-belief alternative is relatively low when τ is low and grows as τ increases. When τ is infinity, the strategy is extreme exploration; all alternatives will be selected with the same probability neglecting beliefs. For example, when beliefs are (0.4, 0.5, 0.6), the choice probabilities are (0, 0, 1) with τ near zero, (0.02, 0.12, 0.87) with τ=0.5, (0.09, 0.24, 0.67) with τ=1, and (0.33, 0.33, 0.33) with τ=infinity.

Results and Discussion

We use simulation studies to examine the mechanism of initial belief in the learning process based on the multi-armed bandit model. We use an exponential payoff distribution with the mean parameter of 0.1. The distribution is similar to that used by Uotila (2017). Only a small number of alternatives carry a high probability of success, so finding superior alternatives is critical. We set the number of periods to 500 and the number of alternatives to 30.

Most simulation studies on exploration and exploitation have matched initial beliefs to the average payoff distribution. However, deviating from the average can improve the performance of exploration strategies (Sutton & Barto, 1998). This study examines the pattern and mechanism of the improvement.

We test the model over a wide range of initial belief (Q0) landscapes (from 0 to 1) and determine the optimal exploration level (τ) for each initial belief setting. The number of runs of simulation for each initial belief-exploration level combination is 10,000.

Table 1 presents the cumulative rewards for different initial beliefs and exploration levels. The average success probability of the payoff distribution is 0.2. When initial belief is set to this 0.2 (the actual average success probability), the optimal level of exploration is 0.6 with a cumulative reward of 331.1. However, if we deviate from initial belief by 0.2, the global optimum of 345.4 can be obtained with initial belief of 0.6 and an exploration level of 0.2. This result indicates that we can improve the reward by increasing initial belief from the true average and decreasing the exploration level. The percent increase in reward was approximately 4.32%, which is considerable in most industry contexts.

Table 1 Cumulative Reward For Different Initial Beliefs (Q0) And Exploration Levels (τ)
	Q 0=0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
τ=0	187.6	222.8	292.4	315.6	332.1	336.8	341.7	344.9	344.8	341.5	335.8
0.1	197.9	232.3	298.9	319.3	333.1	340.2	343.7	343.7	345.2	341.3	339.9
0.2	217.4	251.8	309.3	328.1	336.7	341.7	345.4	343.2	341.2	341.1	341.5
0.3	237.1	269.5	318.3	332.5	338.0	342.6	342.3	338.7	338.1	337.8	336.8
0.4	254.2	284.8	324.0	336.1	340.6	340.2	341.3	337.4	334.4	331.7	332.1
0.5	272.7	295.3	330.1	335.2	336.6	338.9	333.0	330.4	329.3	323.8	332.9
0.6	285.6	305.2	331.1	334.5	333.1	331.4	327.5	323.3	320.2	316.8	319.3
0.7	293.5	311.3	329.5	332.0	326.3	325.0	319.2	317.2	312.1	309.6	308.4
0.8	300.4	314.6	327.5	324.5	321.5	316.7	314.3	308.0	299.9	299.9	301.2
0.9	304.2	314.6	318.2	315.8	312.7	305.5	302.3	298.3	293.3	290.4	291.4
1	305.2	314.4	313.7	309.2	304.7	299.2	292.0	289.1	284.7	277.0	279.0

The results also reveal the pattern of rewards according to exploration level and initial belief. For a given initial belief, the optimal reward is achieved not with an extreme exploration level but with a moderate exploration level. For instance, when initial belief is 0.3, the optimal exploration level is 0.4, not 0 or 1. Consequently, the reward has an inverted U-shaped pattern in the exploration level, which confirms the results of previous studies that a balance between exploration and exploitation is critical (March, 1991, Posen & Levinthal, 2012).

Similarly, for a given exploration level, the reward has an inverted U-shaped pattern for initial belief. For example, when the exploration level is 0.5, the reward is maximal at initial belief of 0.4. Therefore, setting initial belief to an appropriate level is essential. The results also demonstrate that, as initial belief increases, the optimal exploration level decreases. For example, with initial beliefs of 0, 0.3, and 0.6, the corresponding optimal exploration level decreases from 1 through 0.4 to 0.2.

This study examines the underlying mechanism of the improved performance of the strategy using higher initial belief and lower exploration than the strategy with initial belief of the true average success probability. Hereafter, S1 denotes the strategy with initial belief of 0.2 and an exploration level of 0.6 (the optimal strategy for initial belief matched to the average payoff distribution), and S2 denotes the strategy with initial belief of 0.6 and an exploration level of 0.2 (the optimal strategy for initial belief deviated from the average payoff distribution).

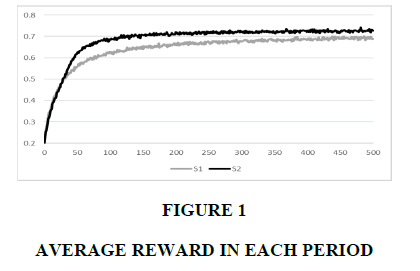
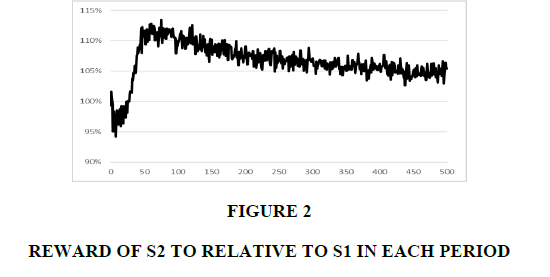
We first examine the average reward in each period. Figure 1 illustrates the average rewards of S1 and S2, while Figure 2 illustrates the relative reward of S2 compared with S1. The relative reward decreases to 95% in the initial periods, indicating that S1’s reward is larger than S2’s. After period 30, S2’s reward exceeds S1’s, and the relative reward increases to and remains at approximately 113% in period 60. After period 60, S2 is still superior to S1 but the gap between S2 and S1 decreases. The relative reward decreases to and remains at 105% after period 400. S1 is superior to S2 in initial periods, and then S2 becomes dramatically superior. However, the gap decreases and stabilizes.

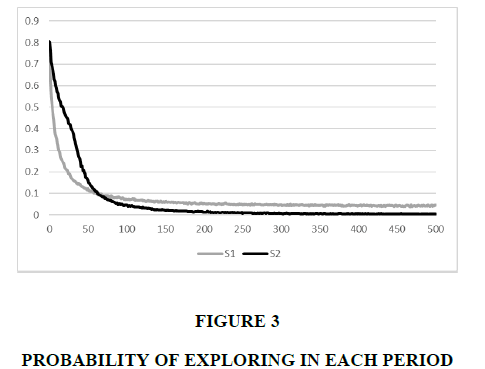
We investigate the differences in the reward patterns by examining the probability of exploring - the probability of not selecting the top 10% alternatives in terms of belief, denoted by PE. Thus, PE indicates the tendency to search for potentially superior alternatives and forgo the currently believed good alternatives.

Figure 3 illustrates the PEs of S1 and S2 in each period. Initially, the PEs are high because of a lack of knowledge, then rapidly decrease as knowledge is gathered, and finally converge at some moment. For the first 60 periods, PE2 (PE of S1) is larger than PE1 (PE of S2). PE1 then becomes larger than PE2, indicating that S1 explores more new knowledge than S2 in the early period, and S1 explores less than S2 afterward.

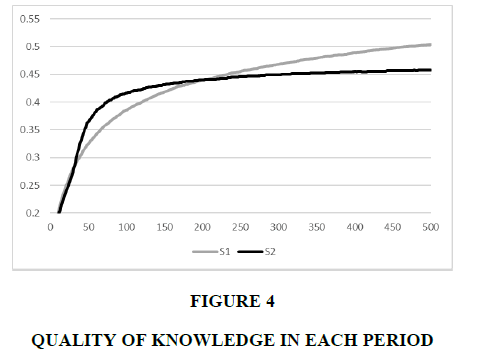
Figure 4 illustrates the quality of knowledge defined as the proportion of alternatives with a top 10% belief to the actual alternatives with a top 10% success probability, denoted by QK. In the initial periods, QK1 and QK2 are similar; however, during periods 40 and 200, QK2 is larger than QK1. After period 200, QK1 is larger than QK2. This result implies that S1 acquires more knowledge in the early stage than S2 but exploits the knowledge in the latter stage. In contrast, S1 tries to gather more knowledge, continuously losing the opportunity for exploitation.

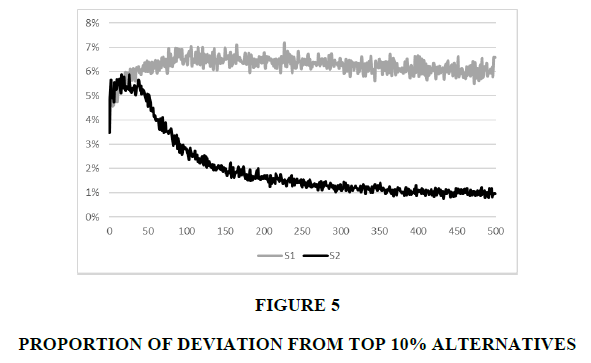
S1’s average reward is lower than S2’s even in the latter stage with more knowledge based on the proportion of selecting the non-top 10% alternatives in period t+1 after selecting the top 10% alternatives in period t, as depicted in Figure 5. In the initial periods, those proportions of S1 and S2 are similar, but the proportion of S2 decreases to approximately 1%. In contrast, that of S1 converges to approximately 6%. Consequently, S2 deviates from superior alternatives and explores other alternatives, even after gathering sufficient knowledge.

Maintaining optimal balance is critical for decisions during exploration - exploitation learning. A decision-maker can increase knowledge by exploring potentially superior alternatives, but the currently-known optimal alternatives must be forgone. In contrast, selecting the alternatives with the highest belief will provide a guaranteed reward but reduce the opportunity to increase knowledge.

Manipulating initial belief can improve performance by mitigating the exploration - exploitation tradeoff (Sutton & Barto, 1998). This study investigates the mechanism of the effect of changing initial belief. For the highest performance, it is crucial to gather more knowledge in the early stage and exploit that knowledge in the latter stage. If initial belief is identical to the actual average success probability, the optimal strategy tends to explore with a high probability, possibly hindering additional improvement. Changing initial belief can resolve this problem.

We demonstrate that increasing initial belief and decreasing the exploration level can improve the cumulative reward. Setting initial belief higher than the actual average success probability leads to a difference between the estimated success probability and belief, which drives frequent exploration in the initial periods. This new strategy explores more in the initial periods than the original strategy, resulting in fewer rewards. However, based on the knowledge gathered during the initial periods, the new strategy improves the quality of knowledge during the early stage, increasing rewards.

After the estimated success probability converges to the true success probability, the low level of exploration strategy encourages the exploitation of current knowledge. Therefore, the new strategy reduces the probability of exploring after the initial periods and uses the acquired knowledge by selecting superior alternatives. In contrast, the original strategy using the actual average as initial belief tends to explore continuously, leading to a higher quality of knowledge than the new strategy in the latter stage. However, it does not exploit the acquired knowledge and frequently deviates from superior alternatives after selecting them. Therefore, its average reward after the initial periods is less than that of the new strategy.

Conclusion

This study assumes a stationary environment where the success probabilities of alternatives do not change over time. However, they might change over time, which will erode the usefulness of acquired knowledge. Further studies should examine the impact of changing initial belief in such dynamic environments.

References

Bubeck, S., & Cesa-Bianchi, N. (2012). Regret analysis of stochastic and nonstochastic multi-armed bandit problems.arXiv preprint arXiv:1204.5721.

Denrell, J., & March, J.G. (2001). Adaptation as information restriction: The hot stove effect.Organization Science,12(5), 523-538.

Gans, N., Knox, G., & Croson, R. (2007). Simple models of discrete choice and their performance in bandit experiments.Manufacturing & Service Operations Management,9(4), 383-408.

Gittins, J.C., & Jones, D.M. (1974). A dynamic allocation index for the sequential design of experiments. In J. Gani, K. Sarkadi, and I. Vincze (eds.), Progress in Statistics, pp. 241–266. North-Holland, Amsterdam–London.

Kaelbling, L.P., Littman, M.L., & Moore, A.W. (1996). Reinforcement learning: A survey.Journal of artificial intelligence research,4, 237-285.

Levinthal, D.A., & March, J.G. (1993). The myopia of learning.Strategic management journal,14(S2), 95-112.

Luce, R. (1959). Individual Choice Behavior: A Theoretical Analysis, Wiley, New York.

Luger, J., Raisch, S., & Schimmer, M. (2018). Dynamic balancing of exploration and exploitation: The contingent benefits of ambidexterity.Organization Science,29(3): 449-470.

March, J. G. (1991). Exploration and exploitation in organizational learning.Organization science,2(1), 71-87.

March, J. G. (1996). Learning to be risk averse.Psychological review,103(2), 309.

March, J. G. (2010).The ambiguities of experience. Cornell University Press.

Moore, A.W., & Atkeson, C.G. (1993). Prioritized sweeping: Reinforcement learning with less data and less time.Machine learning,13(1), 103-130.

Posen, H.E. and Levinthal, D.A., 2012. Chasing a moving target: Exploitation and exploration in dynamic environments.Management science,58(3), pp.587-601.

Robbins, H. (1952). Some aspects of the sequential design of experiments.Bulletin of the American Mathematical Society,58(5), 527-535.

Shahrokhi Tehrani, S., & Ching, A.T. (2019). A Heuristic Approach to Explore: The Value of Perfect Information.Johns Hopkins Carey Business School Research Paper, (19-05).

Sutton, R. S., & Barto, A. G. (1998).Introduction to reinforcement learning. Cambridge: MIT press.

Tadepalli, P., & Ok, D. (1998). Model-based average reward reinforcement learning.Artificial intelligence,100(1-2), 177-224.

Uotila, J., 2017. Exploration, exploitation, and variability: Competition for primacy revisited.Strategic Organization,15(4), pp.461-480.

Urban, G.L., Liberali, G., MacDonald, E., Bordley, R., & Hauser, J.R. (2014). Morphing banner advertising.Marketing Science,33(1), 27-46.