Introduction

Materials Requirements Planning (MRP) is a very useful application area in inventory planning for manufacturing firms. MRP has particular importance to manufacturing inventory systems with dependent demand components (Stevenson, 2018). It has become widely used for managing inventories. The main reasons for this popularity are the benefits gained from its application. According to MRP, the requirements for a part are not expressed as a rate per day, but rather as a vector of dynamic requirements scattered through time. Stocked parts and subassemblies exhibit intermittent usage based on the expected requirements of the assembly line. For instance, the usage of a part that is known to have seasonal demand will fluctuate. It is obvious that such erratic requirements make it desirable to use ordering systems that develop economical orders to absorb this changing and intermittent usage. These ordering rules are known as "lot-sizing techniques" (Schroeder & Goldstein, 2018).

Many lot-sizing heuristics are described in the literature of MRP, also, there are many differing opinions regarding the desirability and the applicability of each (Glock et al., 2014). Some research studies have attempted to demonstrate the superiority of some lot-sizing rules over others, while other studies reported that the economic order quantity is inferior to other lot-sizing techniques such as the Silver-Meal algorithm.

The purpose of this research is to investigate the performance of some popular lot-sizing techniques on the basis of four criteria: ordering cost, carrying cost, total inventory cost, and average inventory.

Theoretical Background

MRP is a logical system for inventory planning and control. MRP systems, as currently known, have been used for several decades. Most of its popularity is due to the advancements in computer technology that enable vast amounts of information to be handled (Krajewski et al., 2016).

During the past decades, MRP has become the prevailing methodology for production and inventory management in manufacturing firms. Earlier, (Orlicky, 1974) found that more than 1000 firms the United States have installed MRP systems. This has changed the way manufacturing inventories and material flows are managed and controlled. As a result, customer service levels improved and inventory investments were reduced.

The concepts that underlie MRP are not new. Aquilano, (2014) cite that the Romans used MRP concepts in planning construction projects, Venetians used them in shipbuilding, and Chinese used them in building the Great Wall.

According to Krajweski (2007) the primary objective of MRP systems is to control inventory levels, to set operating priorities for items, and plan capacity utilization for loading the production system. With respect to inventory, the objectives are: to order the correct part, in the correct quantity, and at the correct time. For operating priorities, the objectives are to order in the correct due date, and to ensure that the due date remains valid. Finally, for capacity planning, the MRP objectives are to plan for a complete and accurate load, and to plan for an adequate time to view future loads.

The aforementioned objectives are the same for Order Point Systems. Order Point Systems are defined as a set of procedures, decision rules, and records intended to ensure continuous physical availability of all items comprising an inventory in the face of uncertain demand (Chase et. al., 2006). However, MRP is more suitable for a manufacturing environment than Order Point Systems, because the first is product oriented, while the second is part oriented.

MRP System Inputs

Four inputs are very essential to the application of MRP system which is:

Demand Report

Demand for end items stems from two sources: regular customer orders, and random or independent demand. Regular customer orders are generated by company marketing efforts. These orders are considered to be firm; they include specific quantities and they have specific dates. Independent demand is forecasted through statistical methods. This demand is subject to further analytical analysis to determine safety stock levels, order points, and order quantities to satisfy predetermined service levels (Silver & Meal, 1973).

Demand for parts and subassemblies come from two sources: dependent and independent. Dependent demand is the net requirement for a particular subassembly or part that is determined by the MRP system. Independent demand comes from sources outside the firm. These sources order parts and subassemblies for service and repairs.

Master Production Schedule (MPS)

The MPS is an aggregate plan stating product needs by classes of items in specific time periods (Florim et al., 2019). The MPS is stated in terms of finished products that are ready for consumption, or in terms of subassemblies that are used in higher levels of the product assembling process. Table (1) depicts an example of a master production schedule for an end item.

Table 1 MPS For An End Item
Period (Weeks)	1	2	3	4	5	6	7	8	9
Required Quantity	200			400		700			800

The span of time the MPS covers is normally related to the cumulative procurement and production lead time for the product in question. The MPS demarcates the entire production program of the firm. Therefore, it contains requirements of end items that the company produces, as well as independent orders for components and subassemblies (Krajweski et al., 2007). Independent demand is usually not part of the MPS, but is fed directly into the MRP system at separate levels.

Inventory Records

The MRP system requires accurate inventory records. If inventory records are not accurate then orders may be greater or less than actual requirements. Either situation is undesirable. Inventory records should also indicate safety stock, the ordering rule, and the lead time of each item, part, or subassembly. Lead Time (LT) is the waiting period between ordering an item and receiving it (Aquilano, 2014). Therefore orders should be placed with lead time in mind. End items, subassemblies, and parts must be checked into inventory when received or completed, and they must be checked out of inventory when they are released for shipping or for usage in higher production stages.

Product Structure

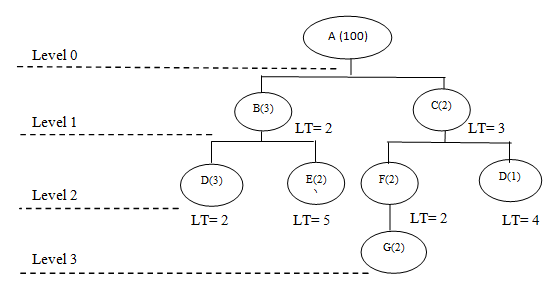
This document shows how the product is put together. It, also, is known as the Bill of Materials (BOM). The BOM contains information that identifies each part or subassembly, and the ratios that parts and subassemblies fit into each other (Harris & Maggard, 1977). Figure 1 depicts the product structure of a product that consists of four levels. The demand on this end item is 100 units, the figures in parentheses refer to the number of parts that go into the parent part (also known as component ratio), while LT refers to the lead time required for producing each part or component.

The MRP Method

According to Swink, et al., (2014) the MRP method is very simple and logical. It starts with end item gross requirements stated in the MPS. End item gross requirements are the sum of regular customer orders and random orders. The MRP system determines end item net requirements by subtracting on hand inventory from gross requirements. Next dependent demand requirements of the components in the product structure are calculated. Component demand (Di) is decided by multiplying the component's ratio times the net requirements of the component that immediately precedes it (Di-1).

MRP determines component gross requirements by summing that component’s dependent demand and external demand. Component net requirements are determined using the same logic as with the end item net requirements. The MRP method goes through the same logic for every production period and updates inventory records after calculating net requirements.

Lot-Sizing Techniques

In this part of the research, we shall describe some popular lot-sizing techniques which are use with the MRP system to minimize the cost of holding inventory while avoiding backorders and stock outs.

The techniques described are the most popular of those developed earlier by Orlicky (1974), Harris (1913), Collier (1980), McLaren (1977), Harris & Maggard (1977), Whybark & Williams (1976), Silver & Meal (1973), Silver, et al., (1998), Silver & Meltunburg (1984), and Wagner & Whitin (1958). Some of these methods are simple in logic while others are more complex.

Fixed-Order Quantity (FOQ)

The Fixed-Order Quantity can be used for any item in the MRP system, but in practice this method is most applicable to items that afford high ordering costs.

The lot size for this method is easy to calculate. It can be determined from historical data, arbitrarily, or by using intuitive/empirical factors. The quantity ordered may reflect exageneous deliberations such as facts not taken into account by any lot-sizing method. Once the quantity is determined, it will be used repetitively. The order quantity does not change unless to meet some unusual conditions of demand. If this occurs, then the quantity will be adjusted. Thereafter, the order quantity returns to the original size.

The advantages of this method are: it is easy to calculate and understand, inexpensive to apply, results in zero stock outs. The disadvantages of this method are: it is limited to items with sufficiently high ordering cost, and it results in carrying excess inventory.

Fixed-Period Requirements (FPR)

The rationale for this technique is similar to that of the fixed-order quantity method. Here, the time interval between orders is constant while the quantity ordered varies. The time interval can be determined arbitrarily or intuitively. The order size is simply the sum of the net requirements for the time interval calculated earlier. Once the time interval is determined it will be used repetitively. The interval is extended when there are zero requirements for a time period. This technique results in high carrying cost because the high average of all items in inventory. However, the order size is inexpensive to calculate, and the method is easy to understand.

The Economic Order Quantity (EOQ)

The EOQ is the classic approach to minimizing inventory costs. The objective of this method is to find the optimum order quantity (Q*) at which total inventory cost is minimized.

The basic assumption that underlies this model are: demand is known with certainty, lead time (L_t) is not permissible, replenishment is instantaneous, order quantities are always the same, unit cost is always constant, planning horizon is in finite, and lead time, demand, and costs are stationary.

Due to the deterministic assumptions of this mode, the only pertinent cost components in the model are the ordering and holding costs. The total cost of inventory consists of holding and ordering costs, and is expressed by the following equation:

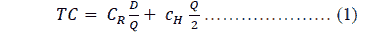
Where: TC=total inventory cost

C_H=ordering cost

C_R=Carrying Cost

D=annual demand

Q=quantity ordered

Taking the first derivative of equation 1, results in the following equation that minimizes the total inventory cost:

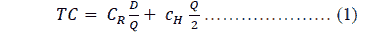
The EQQ approach provides a framework for the analysis of more complex models. In addition, there are situations where this model provides significant inputs for the inventory decision-making process, though this model is never intended for the MRP system because it treats each part as independent from the rest of the items in the product structure. However, it could be applied when the demand volume of parts is large.

The Lot-for-Lot method (L-f-L)

The method is the simplest and most straightforward among all the lot-sizing rules. This method is also referred to as the discrete ordering rule. The lot-for-lot provides a period-by-period coverage of net requirements. The quantity ordered equals the net requirements for the period. Since net requirement are dynamic, the quantity ordered is subject to change, and consequently it must be recomputed whenever necessary. This method minimizes inventory carrying cost, but setup or ordering cost tends to be very high due to frequency of ordering. In practice, this method is recommended for expensive items, or for items that are characterized by highly discontinuous demand.

Least Unit Cost (LUC)

The LUC method and the three techniques that follow have certain characteristics in common. The allow the lot size and the ordering interval to vary. They also share the assumption of discrete inventory depletion at the beginning of each period. This assumption means that a portion of each order is consumed immediately in the first period the order covers. Thus, there is no inventory carrying cost incurred for the portion consumed. Unlike the EOQ technique where the carrying cost is determined by the average inventory on hand, the LUC determines the carrying cost based on the previous assumption.

The lot size for the LUC is determined by a trial-and-error procedure. In determining the lot size, the LUC asks whether the quantity ordered should include present period's requirements only or should the second or the third period's requirements be included in the order. The final decision is based on the lot size the yields the least unit cost (i.e. setup cost plus ordering cost). The deficiency of this method is that is considers one lot at a time, and the unit cost fluctuates between orders. The next three techniques will attempt to overcome this deficiency.

Least Total Cost (LTC)

The LTC model resembles the classic EOQ model presented earlier. It is based on the idea that total inventory cost (order and carrying) for all lots will be minimized if these two costs are as nearly equal as possible. The model strives to achieve this goal by ordering lots when the setup cost/unit is nearly equal to the carrying cost/unit.

The LTC used a more direct procedure than LUC. The Economic Part-Period (EPP) is calculated, then order quantities are selected where the part-period cost is most nearly equal to the EPP. Krajweski et al., (2007) defines the EPP as the quantity of inventory items which if carried in inventory for one period, would result in a carrying cost equal to the cost of setup. The EPP is determined by dividing the inventory carrying cost per unit per time period (CH) into the setup cost (CR).

In general, the LTC approach is favored over the LUC. However, the LTC has a severe drawback. The least total cost is found at a point were carrying cost equals setup cost. The relationship holds true for the classic EOQ model, where inventory depletions is assumed to be continuous. However, LTC is preferred over LUC due to its smaller computation burden and to its tendency to develop ordering patterns that result in lower inventory holding and ordering costs.

The Part-Period-Balancing (PPB)

The PPB model employs the same logic as the LTC. The computation procedure of the lot size is similar to the LTC except for one adjustment referred to as look-ahead/look-back. The objective of this adjustment is to prevent stock covering peak requirements from being carried for long periods, and to avoid orders being initiated for periods characterized with low requirements. In many instances the LTC and the PPB yield the same results.

The PPB takes the results of the LTC approach for a particular order and looks ahead at the net requirements for the periods following those covered by the order. If it seems more economical to increase the size of the first order, to cover another period's requirements than to include it in the second order, then the LTC lot will be increased by that amount. Consequently, the second order will be keyed to a new time period other than the period determined by the LTC method.

The look-back test is performed only if the look-ahead test fails (i.e. yields identical results as the LTC). This test looks back into the earlier order lots to see if it is more economical to decrease the size of an order than to maintain it at the same size. If the test results in some savings, then the order size will be adjusted. The look-back test, if applicable, results in smaller earlier orders than the LTC.

The look-ahead/look-back tests result in adjustments that affect the entire ordering schedules determined under the LTC method. The savings resulting from these adjustments are sometimes trivial, and may negative. The method may result in many small orders which tend to defeat the logic of the LTC that forms the basis of the PPB approach. The fact that the PPB requires tedious computational effort makes the LTC more attractive.

The Silver-Meal Algorithm (S-M)

The Silver-Meal Algorithm is a new and simple approach to the lot-sizing problem. The authors of this technique claim that it produces, on the average, holding and ordering costs less than 1/2 of 1 percent higher than those produced by the most sophisticated techniques such as the Wagner-Whitin algorithm. The following is the method used in the computation:

T=1, 2, 3, ………. the time duration that the current order is to last.

M=EEP=CR/CH

Q=order quantity

R&J=quantities to be used in the algorithm

FJ demand in a particular period.

The procedure is:

Step 1

Let T=1

R=demand, period 1=F

Step 2

Is_T² F_T+1>G_T ?

No: Go to Step 3

Yes: Go to Step 4

Step 3

Let T=T+1

Evaluation R=R+F_T

And G_T=G_T-1+(T-1) F_T

Step 4

Calculation of lot size

Q=current value of

Lot- Sizing Evaluation

Several attempts were conducted in the past to evaluate lot-sizing methods under different conditions (Florim, 2019), in this part of the research we shall evaluate the lot-sizing techniques presented previously using the MPS depicted in Table 2 which represents the Gross Requirements of an item, with an ordering cost of $50/order, and a carrying cost of $1/unit/year.

For purposes of comparison, the total inventory cost (ordering cost+carrying cost) for each method is calculated along with the average inventory during the planning horizon. On hand inventory is assumed to be zero at the beginning planning horizon; no safety stock is required with zero lead time.

Table 2 MPS
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	60			90					60
On Hand Inventory (0)	25	15	15	35	35	15	10	0	30	180
Order Releases	60			90					60

Fixed-Order Quantity (FOQ)

Table 3 presents the final MRP schedule for the MPS shown above. An order size of 60 units is determined arbitrarily to cover the requirements of periods 1 through 3. This quantity is raised to 90 in the fourth period to cover the increased requirements in this period.

Table 3 Foq MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
Gross Requirements (GR)	35	10		70		20	5	10	30	180

No. of orders=3

Average Inventory=180/9=20 units

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory x Carrying Cost)=( 3 × 50)+( 180 × 1 )=$ 330.

Fixed Period Requirements

Table 4 shows the final MRP schedule for the MPS presented in Table 2. A fixed order period of 3 is determined randomly. The scheduled order is 115 units to cover the requirements of periods 1-5. The second scheduled order took place in period 6 because there were no requirements in periods 3 and 5. In the 6th period, the FPR returned to its origin, 3. An order of 35 is scheduled in the 6th period to satisfy the need of periods 6-8, and another order of 30 is scheduled in 9th period to cover the requirements of the last period.

The Lot-for-Lot Technique

As we said earlier, the lot-for-lot method is the simplest; Table 4 presents the results of this method.

Table 4 FPR MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	115								30
On Hand Inventory (0)	80	70	70	0	0	35			30	245
Order Releases	115					35			30

No. of orders=3

Average Inventory=245/9=27.2 units

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=(3 × 50)+( 245 × 1 )=$ 395.

Table 5 EOQ MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	45			70		45			45
On Hand Inventory (0)	10	0	0	0	0	25	20	10	25	80
Order Releases	45			70		45			45	205

No. of orders=4

Average Inventory=80/9=9 units (approx.)

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=( 4 × 50)+( 80 × 1 )=$2 80

Table 6 LFL MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	35	10		70		20	5	10	30
On Hand Inventory (0)	0	0	0	0	0	0	0	0	0	0
Order Releases	35	10		70		20	5	10	30	180

No. of orders=7

Average Inventory=0/9=0 units Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=( 7 × 50)+(0 × 1 )=$ 350

The Least Unit Cost Technique

According to this method the order size that covers the requirement for one, two, three periods or more is determined by a trial-and-error rule to achieve the least unit cost (ordering and carrying cost).

With reference to Table 2 and Table 7, suppose that we determine the order size to be 35 units (column 4) to cover the requirements of the first period. This means that this quantity does not incur carrying cost because it will be consumed immediately, and the order is not inventoried for any period (column 3), therefore, the unit and the total carrying cost is zero (columns 5 and 6 respectively). The unit ordering cost is the ordering cost divided by order size (50/35=$1.430, column 7). The total inventory cost consists of the unit ordering and unit carrying costs, which equals to 1.430+0=$1.430. Now assume that we determine that the order size is 45 units (column 4) to cover the requirements of the first and second periods. For this order size, 35 units will be consumed in the first period and 10 units are held in inventory for one period (column 3) to be consumed in the second period.

The unit carrying cost is the total carrying cost (1×10=10) divided by order size (10/45=$0.22, column 6). The unit ordering cost is $50 divided by the order size, or 50/45=$ 1.11. The total inventory cost is: 1.11+0.22=$ 1.33. We notice now that ordering 45 units results in lower total unit cost compared to ordering 35 units. Therefore, we decide to order 45 units to satisfy the needs for the first and second period. The same procedure is repeated for different order size starting from period four, and so on. The analysis of the least unit cost is depicted in Table 7, while the LUC MRP is presented in Table 8.

Table 7 Least Unit Cost Analysis
Period	Gross Req.	Stocking Periods	Order Size	Carrying Cost		Ordering Cost/Unit	Total Unit Cost
				Total	Unit
-1	-2	-3	-4	-5	-6	-7	-8
				(CH x3)	(CH/3)	(CR/4)	(6+7)
1	35	-	35	-	-	1.43	1.43
2	10	1	45	10	0.22	1.11	1.33*
3		2	-	-	-	-	-
4	70	3	115	220	1.9	0.43	2.33
4	70	-	70	-	-	0.71	0.71*
5		1	-	-	-	-	-
6	20	2	90	40	0.44	0.55	0.99
6	20	-	20	-	-	2.5	2.5
7	5	1	25	5	0.2	2	2.2
8	10	2	35	25	0.71	1.42	2.13*
9	30	3	65	115	1.76	0.43	2.19
9	30	-	30	-	-	1.67	1.67*

*=optimal

Table 8 LUC MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	45			70		35			30
On Hand Inventory (0)	10	0	0	0	0	15	10	0	0	35
Order Releases	45			70		35			30	180

No. of orders=4

Average Inventory=35/9=4 units (approx.)

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=( 4 × 50)+(35 × 1 )=$ 235

Least Total Cost

This method resembles the EOQ method because it depends on the principle of making ordering cost equal to carrying cost as much as possible. This method, also, requires less operations compared to the previous method. To determine the order size, an economic factor K is computed. This factor is computed by dividing the ordering cost by the carrying cost. The result represents a sum of inventory that if we hold it, then ordering and carrying costs will be close to each other. In our case, K=50/1=50. Table 9 presents the analysis of the LTC method.

In this table the total inventory cost was computed for different order sizes. Then the order size (45) whose total inventory cost closer to K=50 was selected to cover the requirements of period 1 through 3. The same procedure was implemented for periods 4 through 9. Table 10 presents the LTC MRP schedule.

Table 9 LTC Analysis
Period	Requirements	Storage Periods	Order Size	Cumulative Inventory Cost
-1	-2	-3	-4	-5
1	35	0	35	-
2	10	1	45*	10**
3	-	2	-	-
4	70	3	115	220
4	70	0	70	-
5	-	1	-	40
6	20	2	90	40
7	5	3	95*	55**
8	10	0	10	-
9	30	1	40*	30**

* optimal order size

** total inventory cost is closer to $50.

Table 10 LTC MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	45			95				40
On Hand Inventory (0)	10	0	0	25	25	5	0	30	0	95
Order Releases	45			95				40		180

No. of orders=3

Average Inventory=95/9=11 units (approx.)

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=(3 × 50)+( 95 × 1 )=$ 245

Part Period Balancing

As it was mentioned earlier, this method is an adjustment of the EOQ technique. First the number of orders is determined by dividing the annual gross requirements by EOQ which yield the number of orders per year. Second, the number of months is divided by the number of orders which gives the period between orders. We clarify as follows:

No. of orders=240/45=5.3 orders/year

Time interval between orders=12/5.3=2 periods (approx.)

Using this result and the logic of this method, we obtain the MRP schedule presented in Table 11.

Table 11 PPB MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	45			70		30		35
On Hand Inventory (0)	10	0	0	0	0	10	5	30		55
Order Releases	45			70		30		35		180

No. of orders=4

Average Inventory=55/9=6 units (approx.)

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=( 4 × 50)+( 55 × 1 )=$ 255

The Silver-Meal Algorithm

Using the multiple iterations presented in section 5.9, the Silver-Meal MRP schedule is constructed and shown in Table 12. Due to the paper limit, the iterations were not presented; however, the author is ready to present it upon request.

Table 12 Silver-Meal MRP Schedule
Period	1	2	3	4	5	6	7	8	9	Total
GR	35	10		70		20	5	10	30	180
Scheduled Orders	45			70		20	5	10	30
On Hand Inventory (0)	10	0	0	0	0	0	0	0	0	10
Order Releases	45			70		20	5	10	30	180

No. of orders=6

Average Inventory=10/9=1 units (approx.)

Total Inventory Cost=(No. of Orders × ordering cost)+(On Hand Inventory × Carrying Cost)=( 5 × 50)+( 10 × 1 )=$ 260

Lot-Sizing Performance Evaluation

Table 13 summarizes the results of evaluating the lot-sizing techniques presented in this work. From this table it seems obvious that the performance of the lot-sizing methods is different on four criteria: the ordering cost, the carrying cost, the total inventory cost, and the average inventory. Table 14 ranks the performance of the lot-sizing techniques, from lower to higher, based on these criteria. The FOQ, FPR, and LTC ranked first on the ordering cost criterion. The LFL ranked first on the basis of carrying cost, while the LUC method ranked first on total inventory cost criterion.

Finally, the LFL ranked first on the average inventory basis. The selection of a suitable technique depends on the priority of the company and the trade-offs that can be achieved from each technique. A guide line may be derived from the previous evaluation, if the company is sensitive to ordering cost, then it should select the FOQ, FPR, or the LTC method. If the company wants to incur lower carrying cost, then it should adhere to the LFL method. If the company is sensitive to total inventory cost, then LUC serves better than the other techniques. If the company is interested in low level inventories due to lack of storage area, then the LFL or the S-M serve better in this case.

Table 13 Summary of Analysis
Technique	Ordering Cost	Carrying Cost	Average Inventory	Total Inventory Cost
FOQ	$150	$180	20	$330
FPR	150	245	27	395
EOQ	200	80	9	280
LFL	350	0	0	350
LUC	200	35	4	235
LTC	150	95	11	245
PPB	200	55	6	255
S-M	250	10	1	260

Table 14 Lot-Sizing Techniques Performance Ranking
Criteria
Ordering Cost		Carrying Cost		Total Cost		Average Inventory
FOQ	150	LFL	0	LUC	235	LFL	0
FPR	150	S-M	10	LTC	245	S-M	1
LTC	150	LUC	35	PPB	255	LUC	4
EOQ	200	PPB	55	S-M	260	PPB	6
PPB	200	EOQ	80	EOQ	280	EOQ	9
LUC	200	LTC	95	FOQ	330	LTC	11
S-M	250	FOQ	180	LFL	350	FOQ	20
LFL	350	FPR	245	FPR	395	FPR	27

Concluding Remarks

This study has highlighted the operating characteristics of eight lot-size models considering four criteria: carrying cost, ordering cost, total inventory cost, and average on hand inventory. To achieve this, a review of the most popular lot-sizing techniques was conducted; we also, highlighted the advantages and disadvantages of each method. A case example was used to prepare the MRP schedule according to the logic of each lot-sizing technique, then the performance of each method is measured based on the four criteria mentioned above. The techniques were ranked, from high to low, according to each criterion to provide a guideline for management to view the possible trade-offs between the methods, and to aid management in selecting the appropriate method that coincides with its priorities. No technique dominated the other techniques, some techniques performed best on the basis of total inventory cost, while another performed best on average inventory on hand. Therefore, the selection on any technique to be used depends on management's priorities. The concepts and techniques presented in this study reflects the importance of understanding the relationships among the four criteria and each method, these concepts are critical in selecting, designing, and operating MRP methods. Although the results of this study are limited to the case example applied, it could serve as a basis to study different cost structure and different demand patterns. This study could be extended to include variable lead time, safety stock, and different product structures. In addition, MRP could be coupled with capacity requirement planning to provide more realistic results.

References

Aquilano, C. (2014). Operations and supply chain management, (14^th edition). Pearson, NY, USA.

Google scholar , Indexed at

Chase, R.B. (2006). Operations management for competitive advantage, (11^th edition). Irwin, McGraw Hill, NY, USA.

Collier, D. (1980). A comparison of MRP lot sizing methods considering capacity change costs. Journal of Operations Management, 1(1), 23-29.

Crossref , Google scholar , Indexed at

Florim, W., Dias, P., Santos, A., Varela, L., Madureira, A., & Putnik, G. (2019). Analysis of lot-sizing methods' suitability for different manufacturing application scenarios oriented to MRP and environments. Brazilian Journal of Operations & Production Management, 16(4), 638–649.

Crossref , Google scholar , Indexed at

Glock, C.H. (2014). The lot sizing problem: A tertiary study. International Journal of Production Economics, 155, 39-51.

Crossref , Google scholar , Indexed at

Harris, F. (1913). How much stock to keep on hand, factory. The Magazine of Management, 10, 281-284.

Google scholar , Indexed at

Harris, R., & Maggard, J. (1977). Computer models in operations management. Harper and Row, NY, USA.

Heizer, J., Render, B., & Munson, C. (2017). Operations management: Sustainability and supply chain management, (12^th edition). Pearson, NY, USA.

Krajewski, L., Malhotra, M., & Ritzman, L., (2016). Operations management: Process and supply chain, (11^th edition). Pearson, Boston, USA.

Krajweski, L., Ritzma, L., & Malhotra, M. (2007). Operations management: Process and value chain, (8^th edition). Pearson, NY, USA.

McLaren, B. (1977). A study of multiple level lot sizing procedures for material requirements planning systems. PhD dissertation, Purdue University.

Google scholar , Indexed at

Orlicky, J. (1974). Materials requirements planning. McGraw Hill, NY, USA.

Schroeder, R., & Goldstein, S. (2018). Operations management in the supply chain, (7^th edition). McGraw Hill, NY. USA.

Silver, E., & Meal, H. (1973). A heuristic selecting lot size requirements for the case of a deterministic time varying demand rate and discrete opportunities for replenishment. Production and Inventory Management, 14(2), 64?74.

Crossref , Google scholar , Indexed at

Silver, E. (1998). Inventory management and production planning and scheduling, (3^rd edition). John Wiley & Sons, NY, USA.

Google scholar , Indexed at

Silver, E., & Miltenburg, J. (1984). Two modifications of the silver-meal lot sizing heuristic. Information Systems and Operational Research, 22, 55-69.

Crossref , Google scholar , Indexed at

Stevenson, W. (2018). Operations management, (13^th edition). McGraw Hill, Penn plaza, NY, USA.

Swink, M., Melnyk, S., Cooper, M., & Hartly, J. (2018). Managing operations across the supply chain, (2^nd edition). McGraw Hill, NY, USA.

Wagner, H., & Whitin, T. (1958). Dynamic version of the economic lot size model. Management Science, 5(1), 89?96.

Crossref , Google scholar , Indexed at

Whybark, C., & Williams, J., (1976). Materials requirements planning under uncertainty. Decision Sciences Journal.

Received: 28-Dec-2021, Manuscript No. AEJ-21-8966; Editor assigned: 30-Dec-2021, PreQC No. AEJ-21-8966(PQ); Reviewed: 10-Jan-2021, QC No. AEJ-21-8966; Revised: 20-Jan-2022, Manuscript No. AEJ-21-8966(R); Published: 28-Jan-2022