Keywords

Monetary Policy Transmission Mechanism, Stock Market Channel, Bank Lending, Market Disciplining.

JEL Classifications

E42; E51; E52; G21

Introduction and Background

A country must have a strong banking sector to achieve sustainable economic growth (Onuonga-Okeri, 2014). Recent financial crises across the globe and the repercussions have crushed the confidence of economic agents in the banking system exposing the possible weaknesses of financial systems in channelling resources to their best use (Stephanou, 2010). However, on the other hand Keiding (2016) cites various issues that may expose the extent of limitation on the part of bank regulations in avoiding crises. Firstly, there is generally lack of enough information in the hands of regulators (SARB, 2013) due to limited access to the extent that even if action is taken, it may be too late or may actually be damaging. Secondly, there are cost implications in regulating financial institutions like banks, thereby regulators may simply refrain (Haldane & Madouros, 2012; Hoenig, 2012). Lastly, Keiding (2016) pointed out that there are several parties to the regulatory framework and in some instances, it may not be clear which of these decide upon the action to be taken on the troubled bank (Haldane & Madouros; Mhango, 2014). The latter is the argument held by critics of twin-peak regulatory framework which has been implemented in South Africa since 2013 (SARB, 2013; Gordhan, 2012; KPMG, 2012).

Furthermore, it has been noted that regulatory compliance costs are prohibitively very high (Harle et al., 2010). The stock market, given listed banks, is a potential source of market discipline on these institutions; however, the key questions to be asked are: the stock market able to assess (monitor) the risk of a particular bank and influence the respective management’s behaviour? Can the stock market assess bank risk and influence bank behaviour? Necessary to note is that there are several market players, notably shareholders, subordinated debtors and uninsured big depositors who can exercise the discipline (Romera & Tabak, 2010).

The main argument is that the traditional bank lending channel model, being a demand-oriented model, fails to control for stock market influence on bank lending. This shortcoming can be addressed by incorporating the capital budget model to bank lending in contrast to the traditional bank lending model. This idea is heavily and explicitly popularised by Krainer (2012, 2014) and Deyoung et al. (2015). This paper applies this line of thinking to the South African dataset in an effort to observe the link between stock markets and the banking sector, that is, “whether the stock market with its many eyes can see more clearly the underlying factors for loan supply and demand to the private sector”(Krainer, 2014) to the extent of disciplining banks.

This helps in understanding the conduct of monetary policy, particularly the kind of asset and markets to be targeted with monetary policy stance aimed at stabilising bank lending and contributing to overall economic development. Bank lending challenges’ solution may lie in the manner of monetary policy focus and implementation (Krainer, 2014).

Literature Review

This study is closely related to the theoretical work on capital budgeting model of bank lending, examining how financial institutions should manage their portfolios when they face costs of external financing linked to capital market imperfections. This is in line with the works of Froot et al. (1993) and Froot & Stein (1998). Froot et al. (1993) specifically showed that firms facing costly external finance, stochastic net worth, and attractive future investment opportunities behave in a risk-averse manner. Bank lending is taken as an investment decision, so that like all investment decisions, it has to face a cost of capital snag (Krainer, 2012; 2014). This view stresses the role of the market valuations of bank stocks reflecting the equity cost of capital for banks. According to this view, banks adjust their investments in loans in response to changes in the cash flows (or profitability) associated with the loans and their cost of capital.

On the other hand, the new bank lending channel, hinges on financial innovation which contributed to the developing of the “Originate to Distribute” (OTD) model (van Rixtel & Gasperini, 2013; Pinna, 2014). In principle, these innovations allowed a broader range of investors to access a class of assets hitherto limited to banks (i.e. loans) thereby distributing these risks to financial (capital) markets. As a result, banks’ funding became much more dependent on perceptions of financial markets (van Rixtel & Gasperini, 2013). Across literature, it has been acknowledged that bank capital has an effect on bank lending if the cost of not meeting minimum capital requirements is high and when the equity market is imperfect to the extent that banks cannot easily issue equity in financial distress periods (Gambacorta & Mistrulli, 2004; Altunbas et al., 2009). To put it in perspective, Beltratti & Stulz, (2012) found out that equity prices of banks with more Tier 1 capital performed comparatively well (with regards to loan supply) during the crisis, than low-capitalized banks.

For South Africa, it has long been postulated that the banking sector does not lend much due to low household savings, and the analysis for such behaviour is scant (Ivashina & Scharfstein, 2010). This study contributes to this strand of literature specifically for the South Africa case and emerging economies as stock markets’ effect of bank loans works through both the demand and supply side. The latter is of more interest to this study as it depends on the individual bank’s financial market price and its balance sheet considering its capital position, a component that has seen regulations being upped to preserve creditability of the sector. Sichei (2005) as well as Mishi & Tsegaye (2012) investigated for the case of South Africa, the bank lending channel, taking into account one of the unique features of the banking sector- concentration. Literature on the traditional bank lending channel is vast, at least globally (Bernanke & Gertler, 1995; Kishan & Opiela, 2000; Angeloni et al., 2003; Ehrmann, & Worms, 2004; Gambacorta, 2005; Ashcraft, 2006; Peek & Rosengren, 2010; Gambacorta & Marques-Ibanez, 2011; Simpasa et al., 2014). However, recent strands of literature emerging have pointed to the possibility of stock market channel of the monetary policy transmission mechanism; notable contributors are Cosimano et al. (1999) Sondermann et al. (2009); Krainer (2011, 2012, 2014) for the case of US, UK and Japan, as well as Burdekin & Tao (2011).

Few studies have incorporated both stock prices and bank loans in their empirical modelling (Dale & Haldane, 1995), Mbutor, 2010; Burdekin & Tao, 2011; Krainer, 2011). The development of the stock market is seen as a complement to that of the banking sector (Garcia & Liu, 1999). However, it is still not clear if stock market can best predict bank lending in South Africa due to limited work in this area. Tan & Floros (2012) show that increased volatility of stock markets can result in greater bank performance measured by return on equity and its excess.

Raunig et al. (2014), using panel data found that growth rate in bank loans declines sharply in periods of uncertainty. Uncertainty was proxied by stock prices volatility, with the effect observed to be varying according to individual specific bank characteristics, such as size and liquidity. In sharp contrast to the above, Karim et al. (2012) concluded that stock markets and banking sector are independent based on results from Granger non-causality test in bivariate and multivariate framework, using both monthly and quarterly time series data on Malaysia.

It is imperative to note here, that the South African banking sector albeit highly sophisticated and well-connected internationally, is highly concentrated (Mishi et al., 2016) as measured by the Herfindahl-Hirschman Index (Mlambo & Ncube, 2011; SARB, 2013, 2014; Banking Association of South Africa (BASA) 2011, 2014). This phenomenon makes comparison across groups (accounting for heterogeneity) categorised by size, laudable when modelling issues within this sector. Bank size has been proxied by assets in line with banking sector literature (Bernanke & Gertler, 1995; Kashyap & Stein 1995, 2000; Kishan & Opiela, 2000; Gunji & Yuan, 2010; Mishi & Tsegaye 2012; and Onuonga-Okeri, 2014).

Carrera (2011) notes that different identification strategies have been proposed, including the use of bank-level data to account for heterogeneity in the response of banks to changes in monetary policy. This is underpinned by the belief that banks are price-takers, in that the demand for loans is infinitely elastic, and reacts differently to monetary policy depending on the substitutability among alternative sources of non-deposit finance. Based on this, four banks have qualified to be in the ‘big banks’ categories (natural log (ln) of total assets value is 10 and above), while eight fall into the small banks categories (ln total assets is below 10). Furthermore, the categorisation reflected and upheld the general market assertion that there are big four banks in South Africa, and they have been rightly identified as Absa, First National Bank (FNB), Nedbank and Standard Bank alphabetically (Mlambo & Ncube, 2011; Maredza & Ikhide, 2013).

Methodology

To determine the impact of stock markets on bank lending in South Africa, the specification of bank lending of monetary policy transmission stresses the capital budgeting aspects of bank investments in private loans as in Krainer (2012, 2014). The reduced-form linear specification of the stock market oriented view of bank lending is given by:

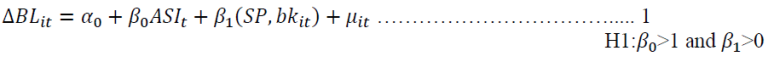
Where

BL = bank lending by each bank (i) in time t.

ASI= All Share index, stock market index in time t.

SP, bk = share price of the specific bank (i) at time (t)

The traditional demand oriented model, on the other hand, follows the following specification:

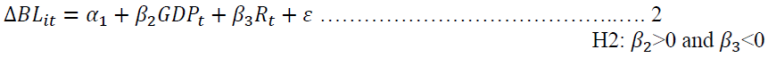
Where, GDP= South Africa’s gross domestic product at time t.

R= monetary rate at time t.

The results of the above specifications are two non-nested hypotheses on this linear bank loan market model.

Variable Definition, a Priori Expectations and Data Sources

BL: Bank lending, the dependent variable, is measured as individual bank loans and advances, to the private sector. The data is obtainable from individual bank financial statements obtained from the Bankscope database.

ASI: All Share Index proxies the profitability generated on the asset acquisitions of loan customers, which will also reflect the investment opportunities of firms, so is the wealth of households. In line with Ibrahim (2006) and Brinkmeyer (2014), a positive and significant relationship between ASI and changes in BL is expected. This variable is obtained from Quantec easydata database.

SP, BK: Share prices for individual banks are used to capture the cost of capital for banks as informed by literature (Krainer, 2014). The data was obtained from Bankscope individual bank’s financial statements. A priori, a positive relationship with bank loans to the private sector is expected, as in Brinkmeyer (2014).

GDP: In theory, the sign of β₂ is ambiguous. In this study, the supply side perspective concurs with a positive β₂ from the traditional argument that higher income of firms and households imply a greater ability to service debt (Ong et al., 2013); therefore, banks are willing to lend more as the default risk is revised down ( Paile, 2014; Jourdan & Ellyne, 2015 for the case of South Africa).

R: Is the money market rate representing the monetary policy stance by the South African Reserve Bank. As the interest rate increase, the demand for loans is expected to decline, hence a negative relationship a priori (Kakes & Sturm, 2002; Liu, 2011; Mishi & Tsegaye, 2012)

Estimation Procedure

a. We run the two regressions separately and the results compared in terms of goodness of fit and stability. The model that better fits the data, which better explains bank lending, identifies the best monetary policy transmission channel in South Africa, the traditional bank lending channel or the existence of the new stock market channel. The latter vindicates the assertion that stock markets have a significant influence on the banks, that is, there is a link between the stock markets and the banks.

b. Non-nested hypothesis tests (J-type tests), as proposed by Davidson and MacKinnon, (1981; 1993) are done. First run the regression in 1 and collect fitted values of BL; the fitted values are included as explanatory in the regression of equation 2. If the estimated coefficient on the fitted values from equation 1 is statistically significant, then reject H₂, if not, then fail to reject H₂. Repeat the procedure for equation 2. The hypotheses being tested are stated in equations 1 and 2 above.

Comparing the non-nested hypotheses implies four outcomes: reject H₁ and fail to reject H₂; reject H₂ and fail to reject H₁; reject both or fail to reject both H₁ and H₂. If both are rejected, then neither model is very useful in explaining bank lending. On the other hand, if it is not possible to reject both, then the data is not opulent enough to differentiate between the two competing models of bank loaning.

Estimations

The models specified above, 1 and 2, are panel in nature, and the key estimation technique is the regression analysis. The study employed panel data models, as opposed to time series models, because of two important reasons. Onuonga-Okeri (2014) while investigating the Kenyan banking sector provided an elaborate account of the advantages of panel data, as well as the different estimation techniques. Panel data models and in particular, the fixed effects model takes into account bank-specific heterogeneity (Gujarati, 2004; Brooks, 2014). The dataset utilised in this study followed a given sample of banks over time, thus providing multiple observations on each entity in the sample, and therefore, following under the category of panel data (Hsiao, 2003; Huang & Lee, 2007). This study benefited from such data structure and related techniques. The fundamental advantage of a panel data set over other formats is the great flexibility in modelling differences in behaviour across entities/ units.

Table 1 below presents the baseline regression results. The variants of the estimation techniques represent pooled ordinary least squares (POLS), 1 and 2; Generalised Least Squares fixed effects techniques (3 & 4) and random effects’ assumed assumption (5 & 6) and least square dummy variable estimation (7 & 8). Based on estimations 1, 3, 5 and 7, the nontraditional bank lending channel is evident in South Africa. The stock markets, at both levels (individual banks and from the side of profitability of the investments, All Share index) significantly explains bank lending. In a similar vein, Ibrahim (2006) concluded that bank loans react positively to the increase in stock prices however, there is no evidence of influence from bank loans to stock prices. The results are also in line with the findings in Krainer (2014).

Table 1: Bank Lending- Traditional (T) vs. Non Traditional (NT) Channel
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
VARIABLES	POLS(NT)	POLS(T)	FE(NT)	FE(T)	RE(NT)	RE(T)	LSDV(NT)	LSDV(T)
jse_alsi	923.2*		1,097***		1,094***		1,097***
	(524.2)		(290.3)		(287.1)		(290.3)
shareprice	11.36***		9.781***		9.847***		9.781***
	(4.026)		(2.942)		(2.886)		(2.942)
2. BFI							-289,961***	-285,978***
							(48,566)	(37,766)
3.BFI							-386,041***	-336,560***
							(44,057)	(42,273)
4.BFI							-380,434***	-342,737***
							(44,275)	(43,452)
5.BFI							67,896	-5,031
							(50,321)	(42,126)
7.BFI							-349,289***	-283,155***
							(47,603)	(39,551)
9.BFI							-65,651	-36,915
							(44,017)	(37,279)
10. BFI							-279,196***	-297,665***
							(59,563)	(51,880)
11. BFI							80,216*	41,949
							(43,394)	(37,279)
gdp		-16,861*		-11,716**		-12,157**		-11,716**
		(8,971)		(5,427)		(5,578)		(5,427)
mmarketr		-17,392***		-25,132***		-24,546***		-25,132***
		(4,712)		(2,943)		(3,018)		(2,943)
8. BFI								-361,654***
								(46,322)
12. BFI								-339,464***
								(43,344)
Constant	14,824	355,098***	6,262	409,468***	-4,625	377,578***	173,129***	583,484***
	(59,149)	(57,870)	(31,555)	(35,571)	(79,981)	(50,856)	(43,880)	(44,353)
Observations	111	162	111	162	111	162	111	162
R-squared	0.131	0.088	0.310	0.331			0.783	0.692
Number of BFI			9	11	9	11

In the case of Nigeria, Oludare et al. (2013) found a positive relationship between returns and NPL, and they interpreted it as: an increase in the amount of NPL ratio will bring about an increase in stock market volatility. However, it can be learnt that there is a link between stock markets and banks fundamentals, especially the loan market variables. Karim et al. (2012) did test causality between stock market and bank loans, and in the case of Malaysia, the authors found strong evidence of no causality running between stock prices and bank loans’ different models and samples. Their explanation for this was the inefficiency of the Malaysia stock market, which is contrary to the South African one (see the literature on South African stock market efficiency (Watson & Rossouw, 2012; Noakes & Rajaratnam, 2014).

The results imply that bank management consider the information presented by stock markets in their investment (extending credit) decisions. In this case, if a bank is performing contrary to its investors’ expectations, their reaction which would affect stock prices will further make bank managers to respond accordingly. In this regard, the stockholders have the ability to impact the investment decision-making by banks. In addition, banks consider the stock market very informative as the All Share Index, reflecting the potential profitability of newly funded ventures, significantly positively explains bank lending. Bank managers are wary of the information asymmetry problems, and the stock markets aggregate and present such information in the form of stock performance which managers can easily discern. Furthermore, Burdekin and Tao (2011) suggest that the stock market could serve as a useful indicator for monetary policy given the significant positive link between its strength and bank lending in China.

Similarly, the traditional model is binding as well. However, the coefficient of growth in GDP is negative, contrary to theory and some evidence in literature. To further investigate this, the volume of turnover on the primary stock market was controlled for; the model improved significantly and the coefficient for primary market turnover was positive. There is a strong negative correlation between primary market turnover volume and GDP growth. On the other hand, money market rates indeed have a negative effect on bank loan demand. This is in line with theory and empirical works in this field. From this analysis it can be argued that in good times (higher economic growth episodes) companies rely on retained earnings than borrowings, hence the negative relationship between bank loan and growth in GDP. On the other hand, stock market development act as a intermediating factors as its inclusion in the model improves the model fit. This further explains the negative coefficient on GDP growth rate.

The fixed or random effects assumption does not make any difference to the results, only that ALSI and GDP are more statistically significant compared to in POLS. On the other hand, the LSDV models confirm that there is a great difference between the banks, as shown by statistically significant intercepts of the individual bank financial institutions (BFI). The comparator firm is BFI (1), which is ABSA. The BFIs that are not having an intercept statistically different from that of ABSA, are the remaining three of the “big four”, FNB, Nedbank and Standard bank, respectively. The behaviour of the big four banks is statistically similar, and all other smaller banks have intercepts that are statistically lower than these, implying the dominance of the big four banks in the South African banking sector. This dominance is also reflected in the widely used measure of concentration, namely, HH-Index which is very high since late 1990s.

Unlike in Krainer (2014) and ignoring Lucas’ (1980) warning, this study controlled for other variables which would help the models fit the data better as outlined below.

Revised Specifications

For the non-traditional (NT) model (stock market channel), the following bank fundamentals obtained in literature were considered:

1. Bank size (size)- the log of bank i’s total assets;

2. Income (lincome)- the total income as a proxy for profitability of each bank;

3. Equity (lequity)- measuring bank capitalization;

4. Total risk capital (lrisk)- capturing the effect of risk capital; and

5. Non-performing loan reserves (lnplres) - proxy for credit risk, from the eyes of the bank managers. This is forward-looking as compared to non-performing loans.

The first set of estimations in Table 1 below failed to distinguish the model that holds for the South African banking sector lending channel.

• jse_alsi= Johannesburg Stock Exchange (JSE) All Share index which represents 99% of the full market cap of all eligible equities listed on the Main Board of the JSE. This is proxy for stock market performance

• shareprice= share price; representing the average price per share for the each individual banking financial institution in the study over the years. The share price is in South Africa currency, Rand

• BFI- banking financial institution- there are 12 banks in the study, Bank 1 is comparator, bank 6 has been omitted due to data. This is a dummy variable ranging from 1-12; 2. BFI is banking financial institution 2 on the list; 3 BFI is Banking Financial Institution 3 on the list, etc. The banks are listed in alphabetical order- see Appendix 1.

Appendix 1 A1: Banking Financial Insitutions (BFI)
Bank	Freq.	Percent	Cum.
ABSA	21	9.33	9.33
African	20	8.89	18.22
Bidvest	21	9.33	27.56
Capitec	15	6.67	34.22
FNB	18	8	42.22
Grindrod	21	9.33	51.56
Investec	21	9.33	60.89
Mercantile	11	4.89	65.78
Nedbank	21	9.33	75.11
Sasfin	20	8.89	84
Standard	21	9.33	93.33
Ubank	15	6.67	100
Total	225	100

• Gdp- gross domestic product, measuring the size of the economy. Growth rate in gdp is captured as percentage change in gross domestic product

• Mmarketr= money market rate, representing monetary policy stance.

Furthermore, the global financial crisis dummy variable was created. In addition, the 1997/98 Asian financial crisis, the 2001/02 minor domestic financial crisis as well as the transition to inflation targeting (IT) monetary policy dummy variables were considered however, they turned out to be immaterial. The motivation for inclusion of all these variables is evidently widespread in literature (Gambacorta, 2005; Simpasa et al., 2014; Onuonga-Okeri, 2014). Literature argues that these are key bank fundamentals which, thus, may be considered by individual institutions before extending loans, or still influence the amount of funds available for lending through influencing the ability to raise funds.

On the other hand, for the traditional (T) loan demand model, general price levels, proxied by inflation is controlled for. This variable captures the macro-economic uncertainties that, in their presence, would hamper demand for loans. Controlling for the above produces the results in Table 2, with size, and non-performing loan reserves positively related to loan supply, while income is negatively linked to loan supply. The latter may be premised on that loan supply is an investment for the bank and increases when other sources of income are limited or low. The results from the revised models, demonstrating the value of controlling other necessary variables, are presented in Table 2.

Table 2 Revised Models: Testing for Stock Market Channel
	(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)
VARIABLES	POLS(T)	FE(NT)	FE(T)	RE(NT)	RE(T)	LSDV(NT)	LSDV (T)	POLS(NT)
size		0.558**		0.428***		0.442***		0.750***
		(0.237)		(0.155)		(0.160)		(0.0907)
jse­_alsi		0.193		0.119		0.106		0.225*
		(0.197)		(0.0744)		(0.0818)		(0.129)
d.shareprice		-9.88e-07		3.28e-05***		3.46e-05***		5.89e-05***
		(3.33e-05)		(1.18e-05)		(1.26e-05)		(2.20e-05)
lincome		-0.692**		0.309*		0.280		-0.652***
		(0.278)		(0.179)		(0.193)		(0.128)
lequity		0.739		0.365***		0.373***		0.470**
		(0.436)		(0.107)		(0.109)		(0.178)
lrisk		-0.439		-0.570***		-0.563***		-0.350***
		(0.270)		(0.0655)		(0.0678)		(0.100)
lnplres		0.498***		0.0679		0.0712		0.498***
		(0.0817)		(0.0600)		(0.0609)		(0.0403)
g_fc	31,122				83,866***	0.0256	83,866***	0.221**
	(48,149)				(27,419)	(0.0617)	(27,419)	(0.108)
2.BFI						0.562**	-285,481***
						(0.223)	(35,099)
3.BFI						-4.617***	-347,164***
						(0.606)	(39,370)
4.BFI						0.209	-366,324***
						(0.214)	(41,748)
5.BFI						-0.130	-12,713
						(0.0900)	(39,170)
7.BFI						0.159	-286,742***
						(0.237)	(36,757)
9.BFI						-0.0805	-36,915
						(0.0824)	(34,638)
10.BFI						0.442*	-282,081***
						(0.257)	(48,302)
11.BFI						-0.413***	41,949
						(0.0890)	(34,638)
gdpc	-12,925		-3,891		-6,191		-6,191
	(9,113)		(15,879)		(5,157)		(5,157)
mmarketr	-22,320***				-29,521***		-29,521***
	(5,750)				(3,320)		(3,320)
infl	13,969		6,115		9,721*		9,721*
	(9,635)		(23,344)		(5,427)		(5,427)
8.BFI							379,609***
							(43,273)
12.BFI							-352,277***
							(40,388)
Constant	295,830***	0.865	158,511	-0.256	356,495***	0.274	534,242***	0.149
	(64,261)	(1.620)	(200,177)	(0.490)	(36,695)	(0.538)	(44,192)	(0.795)
Observations	161	23	30	88	161	88	161	88
R-squared	0.116	0.993	0.004	0.961	0.434	0.997	0.739	0.986
Number of BFI				9	11

ALSI and individual bank stock are still positive and significantly related to bank loan supply, while equity and risk capital are negative and significant in the POLS model. In the same model, the global financial crisis significantly increased bank loan supply- there could have been trade off. The banks facing viability challenges due to non-performing loans, may have considered extending more credit to remain profitable. However, this they did considering the potential profitability of funded investments, as observed from the positive coefficient on ALSI.

The only exceptions remain the performance of T models wherein the GDP turned out insignificant when macro-economic uncertainty (inflation) is controlled for. Inflation itself is only significant and positively related to loan supply in the random effects and LSDV sub-models. Borrowing tends to increase in most uncertain times in line with adverse selection theory. According to Kaya & Meyer (2014), lending is, for the most part a consequence of an adverse economic outlook and fears that a greater share of clients will be unable to service loans in the future (as depicted by low stock market prices or over stock market index). As a response, banks limit loan supply to the best clients by tightening credit requirements.

The above results show improvement in the goodness of fit of the model, with adjusted R-squared values, where applicable, significantly improving. The R-squared values may seem low however, they are in line with studies in related literature and model specifications (Kapan & Minoiu, 2013). However the additional control variables could not help to identify the best bank lending channel at play in South Africa. As a result, up to this point, it is not clear which model best describes bank lending in South Africa between the two, namely: traditional bank lending channel (demand side) or the non-traditional stock market channel. To check further, a non-nested hypothesis test is discussed below.

Non-Nested Hypothesis Testing

As proposed by Davidson & MacKinnon (1981), to compare non-nested hypotheses, there is the J test as the best alternative; especially with linear models as in this case. To understand the approach, assume two non-nested hypotheses that are offered as alternative explanations for L:

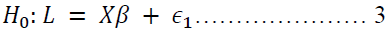
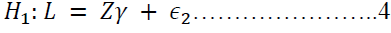
Also consider that the two disturbances are in line with the classical normal model assumptions, where X has k1 and Z has k2 independent non-stochastic regressors (Brooks, 2014). It follows then the “artificial” compound model will take the form:

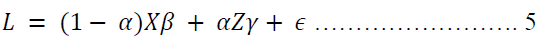
By estimating this model, the non-nested model was tested by one parameter, that is, if α = 0, the composite model breaks to equation (3) and when α = 1, the compound model collapses to equation (4). Theoretically, specification in equation 5 above is appealing and straight forward; however, its empirical application is constrained as the parameters are not identifiable. In literature, and since Davidson & MacKinnon’s (1981, 1993, 2004) proposition, the composite model can easily be replaced by one “in which the unknown parameters of the model not being tested are replaced by estimates of those parameters that would be consistent if the DGP [data generating process] actually belonged to the model they are defined” (Davidson & MacKinnon, 1993), without loss of information or validity.

• Size = measure of individual banking financial institution, proxied by natural log of total assets of that bank

• jse_alsi= Johannesburg Stock Exchange (JSE) All Share index which represents 99% of the full market cap of all eligible equities listed on the Main Board of the JSE. This is proxy for stock market performance in South Africa

• d.shareprice= change in share price of each individual banking financial institution

• lincome= natural log of income generated by the individual banking financial institution (BFI). The income is in South African Rands, then natural log is taken.

• Lequity= natural log of equity for each individual banking financial institution (BFI). Equity is in South African Rands, then natural log is taken

• Lrisk= natural log of risk (proportion of assets as per risk tier ratio provisioning), the assets value are in South African Rands, then a natural log is taken

• Lnplres= natural of non-performing loans and reserves per each individual banking financial institution (BFI). Non-performing loans and reserves are in South African Rands, then a natural log is taken

• g_fc = growth in fixed capital formation in South Africa, measured in percentages.

• gdpc= gross domestic product per capita in South African Rands

• mmarketr= money market rate as proxy for monetary policy stance in South Africa

• infl= inflation rate in South Africa measured from the Consumer Price Index

The results of non-nested model are presented in Table 3 below.

Table 3 Non-Nested Variables Test (J Type Test)
VARIABLES	Baseline (NT)	Baseline (T)	Revised  (NT)	Revised (T)	Baseline J-test (NT)	Baseline J-test (T)	Revised J-test (NT)	Revised J-test (T)
size			0.750***				0.706***
			(0.0907)				(0.0940)
jse-alsi			0.225*				0.218
			(0.129)				(0.132)
d.shareprice			5.89e-05***				6.24e-05***
			(2.20e-05)				(2.22e-05)
lincome			-0.652***				-0.653***
			(0.128)				(0.129)
lequity			0.470**				0.524***
			(0.178)				(0.183)
lrisk			-0.350***				-0.357***
			(0.100)				(0.100)
lnplres			0.498***				0.511***
			(0.0403)				(0.0413)
g_fc			0.221**	31,122			0.289**	81,690*
			(0.108)	(48,149)			(0.115)	(48,139)
jse_alsi	923.2*				1,149**
	(524.2)				(519.6)
shareprice	11.36***				10.24**
	(4.026)				(4.346)
gdpc		-16,861*		-12,925		-25,658**		5,787
		(8,971)		(9,113)		(11,229)		(8,628)
mmarketr		-17,392***		-22,320***		-10,385		-21,790**
		(4,712)		(5,750)		(9,824)		(10,693)
infl				13,969				5,311
				(9,635)				(10,608)
demand1					1.061**
					(0.443)
supply1						1.106***
						(0.261)
demand2							-1.41e-06*
							(8.34e-07)
supply2								71,255***
								(5,991)
Constant	14,824	355,098***	0.149	295,830***	-168,826*	151,858	0.352	-441,926***
	(59,149)	(57,870)	(0.795)	(64,261)	(91,694)	(111,000)	(0.820)	(95,175)
Observations	111	162	88	161	108	108	86	86
R-squared	0.131	0.088	0.986	0.116	0.214	0.220	0.987	0.679
Standard errors in parentheses
*** p<0.01, ** p<0.05, * p<0.1

Four models have been estimated: two baseline (non-traditional which has stock market/ supply side approach vs traditional which has the demand side approach) and two modified (non-tradition vs traditional as define before).

• demand1= residuals of the traditional baseline model used as regressors in the non-traditional baseline specification

• supply1= residuals of the non-traditional baseline model used as regressors in the traditional baseline specification

• demand2= residuals of the traditional modified model used as regressors in the non-traditional modified specification

• supply2= residuals of the non-traditional modified model used as regressors in the traditional modified specification

Thus, to test equation (4), γ in 5 is replaced by its estimate 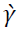obtained by regressing L on Z. If we write 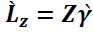the equation to be estimated to test whether α = 0 is

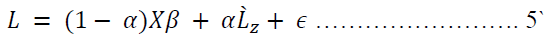
Similarly, to test equation (2), the study estimate 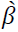by fitting equation (1) to the data and replaced Xβ in (5) by 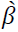, or 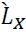. The equation estimated to test (2) as a result then became:

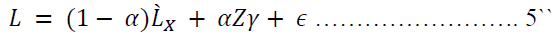
The Davidson and MacKinnon J-test applies the t-test for the estimated coefficients on 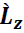in equation (5`) and 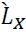in equation (5``). A statistically significant t-statistic on the coefficient of 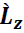rejects H₀ as the appropriate model and a significant t-statistic onthe 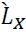coefficient results in the rejection of H₁. Davidson and MacKinnon (1993) show “why the J and P tests (which in [linear models] are identical) are asymptotically valid.”

Comparing the non-nested hypotheses implies four outcomes: reject H₀ and fail to reject H₁; reject H₁ and fail to reject H₀; reject both or fail to reject both H₀ and H₁. If both are rejected, then neither model is very useful in explaining bank lending, on the other hand, if it is not possible to reject both, then the data is not opulent enough to differentiate between the two competing models of bank lending. It is also prudent to take note of some of the weaknesses of the J test that have already been stated in literature. For Godfrey & Pesaran (1983) assert that there are some conditions where the J test is likely to over-reject the true hypothesis, for example, in smaller samples. Moreover, Davidson & MacKinnon (2004) agree that the J test will over-reject, “often quite severely” in finite samples when the sample size is small. In relation to this study, the sample is fairly large enough to worry about this limitation, that is, there are 12 banks over a twenty year period. Based on this, the study continued with the J test on the South African banking sector data.

The results in Table 3 above displaying statistically significant coefficients on added residual variables from each of the other model (demand1, supply1, demand2 and supply2) prove that the two models still hold; however, the performance of other variables in the traditional model is weakened, making the model less robust. Depending on whether other control variables are included or not, either the market rate or GDP growth becomes significant, respectively. The results are, again, inconclusive. Due to this, the omitted variable test in STATA is utilised to check which model exhibits omitted variable problem.

Robustness Checks

In addition to Krainer’s (2014) test for omitted variables, this study made use of the diagnostic test available in STATA as a post hoc analysis. The results (not presented for brevity) show that there is a negative relationship between GDP growth, market interest rate and bank lending. On the other hand stock market based variables, individual bank stock prices and overall stock market performance (JSE-ALSI) positively affect bank lending. The stock market channel model better explains bank lending than the traditional channel as R-squared is relatively higher 0.131> 0.088. This difference is tested statistically using the post hoc options. The post hoc analysis in the form of Ramsey Omitted Variables Test show that for Non-Traditional Channel (stock market) (F(_,_)(3, 105) 0.51; p-value = 0.6753 and vs Traditional Bank lending channel F(_,_) (3,156) 3.29; p-value = 0.0222. The p-value 0.68 > 0.05, we fail to reject null hypothesis and concluded that the non-traditional (stock market) channel has no omitted variables. The p-value 0.02< 0.05, we reject null hypothesis and concluded that the traditional bank lending channel has some omitted variables. It can be concluded that the stock market channel is superior to the traditional bank lending channel in South Africa, just as in the case of Sondermann et al. (2009) and Krainer (2014). Indeed, stock markets do matter for bank loan supply as bank managers derive information about the economy and its prospects from the stock market index as well as considering the strength of their balance sheet through stock prices. This implies that there is great possibility of the existence of stock market discipline of banks in South Africa; a phenomenon tested in future study.

Heteroskedasticity was tested using Breusch-Pagan test, the results confirmed presence of homoscedasticity. Robust standard error estimation was done, which does not alter estimated coefficients; however, due to the change in standard errors, the test statistics provides reasonably accurate p-values (Stock & Watson, 2008). According to Stock & Watson (2003), the rule-of-thumb is to always assume heteroskedasticity.

Summary and Conclusion

The paper estimated the model of stock market lending channel to test the role of stock markets on bank lending. Taking into account various possible estimations, the results point to a significant role played by stock market in determining the lending pattern of banks. The results indicate the presence of stock market channel of monetary policy transmission in South Africa, thus vindicating the appropriate intermediate target for the central bank to be price level, with price stability being the ultimate goal (as the current Inflation Targeting framework). Furthermore, the results point to the possibility of stock market discipline of banks as, indeed, stock markets have been found to be significantly linked to banks operations as being an information aggregator and provider. Overall, the results confirm that stock markets influence bank lending and thus, there exists a stock market lending channel for the monetary policy transmission in South Africa. These results are in line with Chatterjee’s (2015) findings, where the interaction between stock market liquidity and bank loans was determined as prevalent to the extent that it poses challenges to the existing banking literature on monetary transmission mechanism in several ways. Such findings have implications for the monetary policy transmission conduct as they close a gap in literature on the weakness of monetary policy effect on bank lending (Kashyap & Stein, 2000).

The capital budgeting model proposed by Krainer (2012, 2014) and tested in this study is in line with a bank equity model postulated by Bolton & Freixas (2006). Their model shows that monetary policies do not affect bank lending. However, monetary policies affect bank equity capital and corporate financing through changes in loans to corporate bond spreads. Due to this link, the expected relationship is positive, as bank equity decreases, loans become scarce. In this study (Table 2), a positive relationship was, indeed, found. Moreover, Kapan & Minoiu (2013), for the case of Japan, concluded that banks with strong balance sheets were better able to maintain lending during the crisis, as higher and better quality capital was key in mitigating the crisis effect on bank lending.

To support the link between stock market and bank lending, Johnson (2006) argued that agents consider underlying economic uncertainties before trading. This creates a causal link between state of the economy and stock market fundamentals and, in turn, bank balance sheet management. Ibrahim (2006) upholds a similar line of thinking, arguing that the health of the banking sector depends crucially on stock market stability. On the other hand, Chatterjee (2015) argued that stock market liquidity not only determines implied cost of capital for borrowers but also governs the supply side via terms for external funds, such as deposits and bank borrowings. Unlike Ibrahim (2006), this study uses individual bank stock prices as well as the stock market index.

Indeed, stock markets proved to be an informative sector to the supply of bank loans. Banks observe their financial soundness by checking their how their share prices are performing as well as how the stock markets, in general, are performing (measured by All share index) before deciding on how much to lend. This finding points to the possibility of stockholders having the ability to impact the investment decision-making by banks. The traditional lending channel was found to be less robust than the new bank lending channel in the J-type test used to compare the goodness of fit of the models.

Stock market variables were identified as statistically significant missing variables in the traditional bank lending model. Using the Ramsey omitted variable test, the traditional bank lending channel produced a p-value of 0.02 which is less than 0.05 and therefore, we rejected the null hypothesis (model has no omitted variables) in favour of the null that the channel has some omitted variables. On the other hand, a p-value of 0.68 on the stock market channel led to failure to reject the null that the model has no omitted variables, and thus concluding that the model is well specified, and there are no missing variables.

The capital budgeting model is confirmed for the case of South Africa by these results. Quality capital increases lending and in line with Ibrahim (2006), the health of the banking sector depends on stock market stability. Stock markets and the banking sector are found to be complementary to each other in line with the financial services’ view. The first condition for effective market monitoring is that markets must be open. South Africa had made strides towards this as the markets are highly developed, sophisticated and efficient, ranking favourably high globally. The authorities should continue to keep abreast with international regulations and standards, for example implementation of the Basel Accords as this assist in stabilizing the financial system as well as allowing for coordination among various actors in the system (these includes banks and stock markets). On the other hand, disclosure of capital structure and risk exposure should be timely and readily available. The Basel Accords recommendations, of which South Africa keenly implements, support more disclosure of information by banks to allow market participants to monitor the institutions’ fundamentals

Acknowledgements

The authors wish to acknowledge the comments and insights form the reviewers. Funding: Syden Mishi wish to acknowledge funding by National Research Foundation GRANT UID: 89077. The standard disclaimer applies.

References

1. Allen, F., & Carletti, E. (2008). Mark-to-Market accounting and liquidity pricing. Journal of Accounting and Economics, 45(2-3), 358 - 378.
2. Altunbas, Y., Gambacorta, L., & Marques-Ibanez, D. (2009). Securitisation and the bank lending channel. European Economic Review, 53(8), 996-1009.
3. Angeloni, I., Kashyap, A., & Mojon, B. (2003). Monetary Policy Transmission in the Euro Area. Cambridge University Press, Cambridge.
4. Ashcraft, A.B. (2006). New evidence on the lending channel. Journal of Money, Credit, and Banking, 38(3), 751-76.
5. Banking Association of South Africa (BASA). (2011). South African Banking Sector Overview; Available online: http://www.banking.org.za/index.php/our-industry/2011-south-african-banking-sector-overview/
6. Banking Association of South Africa (BASA). (2014). South African Banking Sector Overview; http://www.banking.org.za/index.php/our-industry/2014-south-african-banking-sector-overview/
7. Beltratti, A., & Stulz, R.M. (2012). The credit crisis around the globe: Why did some banks perform better? Journal of Financial Economics, 105(1), 1-17
8. Bernanke, B.S., & Gertler, M. (1995). Inside the black box: The credit channel of monetary policy transmission. Journal of Economic Perspectives, 9(1), 27-48
9. Bolton, P., & Freixas, X. (2006). Corporate finance and the monetary transmission mechanism. Review of Financial Studies, 19(3), 829-870.
10. Brinkmeyer, H. (2014). Drivers of Bank Lending: New Evidence From the Crisis. Wiesbaden: Springer Gabler
11. Brooks, C., (2014). Introductory Econometrics for Finance. Cambridge: Cambridge University Press
12. Burdekin, R.C.K., & Tao, R. (2011). An ABC Guide to Provincial Lending Patterns in China. Chinese Economy, M.E. Sharpe, 44(5), 34-54
13. Carrera, C. (2011). The Bank Credit Channel in Peru: Evidence and Transmission Mechanism. Economic Studies Magazine, (22), 63-82.
14. Chatterjee, U.K. (2015). Bank liquidity creation and asset market. Journal of Financial Stability, 18, 139-153.
15. Cosimano, T.F., Fullenkamp, C., & Chami, R. (1999). The Stock Market Channel of Monetary Policy. IMF Working Papers 99/22, International Monetary Fund.
16. Dale, S., & Haldane, A.G. (1995). Interest rates and the channels of monetary transmission: Some sectoral estimates. European Economic Review, 39(9), 1611-1626.
17. Davidson, R. & MacKinnon, J.G. (1981). Tests for Model Specification in the Presence of Alternative Hypotheses: Some Further Results. Working Papers 430, Queen's University, Department of Economics.
18. Davidson, R., & MacKinnon, J.G. (1993). Estimation and Inference in Econometrics. Oxford University Press, Oxford.
19. Davidson, R., & MacKinnon, J.G. (2004). Econometric Theory and Methods. New York: Oxford University Press.
20. Deyoung, R., Gron, A., Torna, G., & Winton, A. (2015). Risk overhang and loan portfolio decisions: Small business loan supply before and during the financial crisis. The Journal of Finance, 70(6), 2451-2488
21. Ehrmann, M., & Worms, A. (2004). Bank networks and monetary policy transmission. Journal of the European Economic Association, 2(6), 1148-71.
22. Froot, K.A., & Stein, J.C. (1998). Risk management, capital budgeting, and capital structure policy for financial institutions: an integrated approach. Journal of Financial Economics, 47(1), 55-82.
23. Froot, K.A., Scharfstein, D.S., & Stein, J.C. (1993). Risk management: Coordinating corporate investment and financing policies. Journal of Finance, 48(5), 1629-58.
24. Gambacorta, L. (2005). Inside the bank lending channel. European Economic Review, 49(7), 1737-1759.
25. Gambacorta, L., & Marques?Ibanez, D. (2011). The bank lending channel: lessons from the crisis. Economic Policy, CEPR; CES; MSH, 26(66), 135-182.
26. Gambacorta, L., & Mistrulli, P.E. (2004). Does bank capital affect lending behaviour? Journal of Financial Intermediation, 13(4), 436-57.
27. Garcia, F.V., & Liu, L. (1999) Macroeconomic determinants of stock market development. Journal of Applied Economics, 2, 29-59
28. Ghiasi, E., Mohseni, R.M., & Shirazi, J.K. (2014). Banking and stock markets in Iran: Are they complements or substitutes, ISADER, 6 (1), 7-20.
29. Godfrey, L.G., & Pesaran, M.H. (1983). Tests of non-nested regression models: Small sample adjustments and Monte Carlo evidence. Journal of Econometrics, 21, 133-154
30. Gordhan, P. (2012). 2012 Budget Speech: S A National Treasury, February 22; Cape Town, South Africa
31. Gujarati, D. (2004). Basic Econometrics. (4th Edition). The McGraw-Hill Companies, New York
32. Gunji, H., & Yuan, Y. (2010). Bank profitability and the bank lending channel: Evidence from China. Journal of Asian Economics, 21, 129-141.
33. Haldane, A., & Madouros, V. (2012). The dog and the Frisbee. Speech at the Federal Reserve Bank of Kansas City's 366th economic policy symposium, "The changing policy landscape", Jackson Hole, Wyoming, 31st August.
34. Harle, P., Luders, E., Peparides, T., Pfetsch, S., Pappensieker, T., & Stegemann, V. (2010). Basel III and European banking: Its impact, how banks might respond, and the challenges of implementation, McKinsey Working Papers on Risk, No 26. McKinsey & Company, November.
35. Hoenig, T. (2012). Back to Basics: A Better Alternative to Basel Capital Rules. Address to the American Banker Regulatory Symposium, Washington DC, 14th September.
36. Hsiao, C. (2003). Analysis of Panel Data (2nd Edition). Cambridge: Cambridge University Press.
37. Huang, Y., & Lee, Y.J. (2007). An improved generalized spectral test for conditional mean models in time series with conditional heteroskedasticity of unknown form. Econometric Theory, 23(01),106-154.
38. Ibrahim, M. (2006). Stock Prices and Bank Loan Dynamics in a Developing Country: The Case of Malaysia. Journal of Applied Economics, 9(1), 71-89.
39. Ivashina, V., & Scharfstein, D. (2010). Bank Lending during the Financial Crisis of 2008. Journal of Financial Economics, 97(3), 319-338.
40. Johnson, T. (2006). Dynamic Liquidity in Endowment Economies. Journal of Financial Economics, 80(3), 531-562.
41. Jourdan, B., & Ellyne, M. (2015). Did the 2005 National Credit Act contribute to an unsecured boom and bust? Unpublished Master’s Dissertation for the University of Cape Town’s Economic Development Programme.
42. Kakes, J., & Sturm, J.E. (2002). Monetary policy and bank lending: Evidence from German banking groups. Journal of Banking & Finance, 26(11), 2077-2092.
43. Kapan, T., & Minoiu, C. (2013). Balance Sheet Strength and Bank Lending during the Global Financial Crisis, IMF Working Paper 13/102; Washington: International Monetary Fund.
44. Karim, B.A., Lih, L.S., & Karim, Z.A. (2012). Bank loans and stock prices: An empirical evidence. Aceh International Journal of Social Sciences, 1(2), 48-52
45. Karim, D., Liadze, I., Barrell, R., & Davis, E. (2012). Off-balance sheet exposures and banking crises in OECD countries. Journal of Financial Stability, 9(4), 673-681.
46. Kashyap, A.K., & Stein, J.C. (1995). The impact of monetary policy on bank balance sheets. Carnegie Rochester Conference Series on Public Policy, 42, 151-95.
47. Kashyap, A.K., & Stein, J.C. (2000). What do a million observations on banks say about the transmission of Monetary Policy? American Economic Review, 90, 407-428.
48. Kaya, O., & Meyer, T. (2014). Tight bank lending, lush bond market New trends in European corporate bond issuance; Current Issues: Global financial markets, Editor: Dallmeyer, J. Deutsche Bank Research.
49. Keiding, H. (2016). Economics of Banking. Palgrave: MacMillan.
50. Kishan, R.P., & Opiela, T.P. (2000). Bank size, bank capital, and the bank lending channel. Journal of Money, Credit, and Banking, 32(1), 121-41.
51. KPMG. (2012). 2012 Banking Industry Outlook Survey: Regulatory Change Spans the Enterprise. Retrieved from www.kpmg.com/us/bankingindustry
52. Krainer, R. (2011). On the Role of a Stock Market in the European Bank Loan Market: A Study of France, Germany, and the Euro Area, an invited presentation at the 29th SUERF Colloquium on New Paradigms in Money& Finance, Brussels, 11-12 May 2011.
53. Krainer, R. (2012). Is there a Stock Market Channel for Bank Lending in the Euro Area? Banque de France Working Paper No. 221
54. Krainer, R. (2014). Monetary policy and bank lending in the euro area: is there a stock market channel or an interest rate channel? Journal of International Money and Finance, 49(B), 283-298.
55. Liu, L. (2011). Monetary policy, bank size and bank lending. Evidence from Australia, MPRA Paper 35033, University Library of Munich, Germany.
56. Lucas, R.E. Jr. (1980). Methods and Problems in Business Cycle Theory. Reprinted in Lucas (1981): Lucas, R. E., Jr. (1981), Studies in Business-Cycle Theory. Oxford: Blackwell.
57. Maredza, A., & Ikhide, S.I. (2013). Dealing with the challenge of generating employment in South Africa: Does banking sector efficiency matter? International Business and Economics Research Journal, 12(11), 1361-1372.
58. Mbutor, O.M. (2010). Can Monetary Policy enhance remittances for economic growth in Africa? The case of Nigeria. Journal of Economics and International Finance, 2(8), 156-163.
59. Mhango, M. (2014). Twin Peaks is not for SA, Fin24. Retrieved from www.fin24.com/companies/financial-services
60. Mishi S., Sibanda K., & Tsegaye A. (2016) Industry concentration and risk taking: Case of South African Banking sector. African Review of Economics and Finance, 8(2).
61. Mishi, S., & Tsegaye, A. (2012). The role of banks in monetary policy transmission in South Africa.Economics Research Southern Africa, ERSA, Working paper: 295. Cape Town, South Africa.
62. Mlambo, K., & Ncube, M. (2011). Competition and efficiency in the banking sector in South Africa. African Development Review, 23(1), 4-15
63. Noakes, M.A., & Rajaratnam, K. (2014). Testing market efficiency on the Johannesburg Stock Exchange using the overlapping serial test. Annals of Operations Research, 1-28
64. Oludare, S., Olagunju, M., & Adelodun, O. (2013). Stock market volatility and non-performing loans: evidence from stocks of the Nigerian banks. African Finance Journal, 15(1), 82-104 
65. Ong, R., Haffner, M., Wood, G., Jefferson, T.M., & Austen, S.E. (2013). Assets, debt and the drawdown of housing equity by an ageing population, AHURI Final Report no. 153, Australian Housing and Urban Research Institute, Melbourne.
66. Onuonga-Okeri, S. (2014). The Analysis of Profitability of Kenya`s Top Six Commercial Banks: Internal Factor Analysis. American International Journal of Social Science, 3, 5. 
67. Peek, J. & Rosengren, E.S. (2010). The Role of Banks in the Transmission of Monetary Policy, In The Oxford Handbook of Banking, Allen Berger, Philip Molyneux, and John Wilson, eds. Oxford: Oxford University Press.
68. Paile, K. (2014). The Impact of the National Credit Act on Household Debt Levels in South Africa From: http://wiredspace.wits.ac.za/handle/10539/14754 Unpublished Thesis & Dissertation, WITS
69. Raunig, B., Scharler, J. and Sindermann, F. (2014). Do Banks Lend Less in Uncertain Times? Working Paper 194. Oesterreichische Nationalbank.
70. Romera, M.P., & Tabak, B.M. (2010). Testing for market discipline in the Brazilian banking industry. Banks Bank System, 5(3), 112-128.
71. Sichei, M. (2005). Bank-lending channel in South Africa: Bank-level dynamic panel data analysis. University of Pretoria, working paper: 2005-10.
72. Simpasa, A., Nandwa, B., & Nabassaga, T. (2014). Bank Lending Channel of Monetary Policy Transmission in Zambia: Evidence from Bank-Level Data, Working Paper Series N° 211 African Development Bank, Tunis, Tunisia.
73. Sondermann, D., Bohl, M.T., & Siklos, P.L. (2009). The Euro Area Stock Market Channel: Does One Size Fit All?  Finance Research Letters, 6(4), 230-235.
74. South African Reserve Bank (SARB). (2013). Banking Supervision Department Annual Report.
75. South African Reserve Bank (SARB). (2014). Banking Supervision Department Annual Report.
76. Stock J.H., & Watson M.W. (2008). Phillips Curve Inflation Forecasts, NBER Working Papers 14322, National Bureau of Economic Research, Inc.
77. Stephanou, C.  (2010). Rethinking market discipline in banking lessons from the financial crisis. Policy Research Working Paper 5227, World Bank.
78. Tan, A.Y., & Floros, C. (2012). Stock market volatility and bank performance in China. Studies in Economics and Finance, 29(3), 211-228.
79. Van Rixtel, A., & Gasperini, G. (2013). Financial crises and bank funding: Recent experience in the euro area, BIS Working Papers 406, Bank for International Settlements.
80. Watson, S., & Rossouw, J. (2012). JSE efficient and share price reaction to forced financial restatements. Journal of Economic and Financial Sciences, 5(2), 417-435.