Predicting Bankruptcy of Selected Indian Steel Companies - A Multinomial Regression Approach

Sheeba Kapil; Aniruddha Ghosh

Research Article: 2022 Vol: 26 Issue: 5

Predicting Bankruptcy of Selected Indian Steel Companies - A Multinomial Regression Approach

Aniruddha Ghosh, Indian Institute of Foreign Trade

Dr. Sheeba Kapil, Indian Institute of Foreign Trade

Citation Information: Ghosh, A., & Kapil, S. (2022). Predicting bankruptcy of selected indian steel companies - a multinomial regression approach. Academy of Accounting and Financial Studies Journal, 26(5), 1-14.

Abstract

The Indian steel industry is facing a mammoth liability from its outstanding loans amounting to Rs three lakh crore in various banks. To explore this anomaly, a study has been conducted to analyse the bankruptcy risk of 150 steel companies in India. The first objective was to identify the number of steel companies lying in the distress zone. The second objective was to find whether the distress condition has deteriorated more in large companies or in small and medium companies. The third objective was to develop a bankruptcy prediction model using the Multinomial Logistic Regression to assess the authenticity of the bankruptcy risks these steel companies face. Emphasis was also made to explore the major reasons behind the distressed condition of the various types of steel companies. Altman Z-score model was used as a proxy to determine the level of distress among the various selected Indian steel companies. Thereafter, Multinomial Logistic Regression Model is used for predicting the accuracy of the bankruptcy among the steel companies. Results include that bankruptcy risk has a significant relationship with debt-equity level and level of working capital of the company. The overall model explanation was 81.07%. Other outcomes include lower operating margin level, and lower level of net profits as well. This study again proves that excessive usage of debt is hazardous for the survival of the company. The study also shows that the prediction capability of the model is significantly strong and is better for predicting bankruptcy risks among steel companies. It also provides the provision for further research regarding the introduction of additional explanatory variables and qualitative variables to improve the model.

Keywords

Bankruptcy Prediction, Altman-Z Score, Multinomial Logistic Regression Model.

Introduction

The bankruptcy of several companies within an industry hurts the sustainable affluence of people both economically and socially. The listed iron and steel industry in India has also similar repercussions. This study will help us to understand the prosperity of the listed iron and steel companies in India in the long run. It would also help us to understand whether the distress condition has deteriorated more in large companies or in small and medium companies, which will answer the dilemma of sustainability of the above companies (Amoa‐Gyarteng, 2019; Oude Avenhuis, 2013; Altman et al., 2019). Thus, this article will provide development opportunities for small and medium iron and steel companies to foster growth (Mangena & Pike, 2005). A recent report on bankruptcy filings submitted by Insolvency and bankruptcy board of India (IBBI) almost However, predicting the bankruptcy of steel companies is not a new one. The main reasons for conducting this study lie in the following facts India’s steel production came down 0.7% to 45.537 million tonnes, whereas consumption grew 4.1% to 39.147 metric tonnes in the half-year ended September 2015 of the fiscal ending 31st March 2016. Imports continued to hurt the industry, rising 43.4% to 5.501 metric tonnes, while exports decreased 26.4% to 2.024 metric tonnes in the period. So adverse revenue situations, high debt levels, and increased borrowing costs lead to the assessment of bankruptcy risk of the Indian steel companies listed in the BSE. To overcome this adverse situation, this study approaches to propose a model through multinomial logistic regression to predict the bankruptcy level of the steel manufacturing companies in India (Singh, 2004). This study firstly introduces the topic and the present scenario in the steel industry in India, followed by a brief literature review, then by the methodology followed to carry the research forward, then by findings and discussion and lastly, the conclusion which epitomizes the whole study including the limitations as well (Dambolena & Khoury, 1980).

Literature Review

There are several works done by many authors on bankruptcy prediction, however, among them, Altman’s Z score model of analyzing bankruptcy is the most popular one (Bellovary et al., 2007). The bankruptcy work started way back during the 1930’s, when the authors started to the analyze financial profile of companies with risk of business failure. Most of the research work done till 1960’s included univariate (i.e., individual ratio) studies, among the studies Beaver’s study in 1966 was the most popular one. In 1968, Altman suggested the first multivariate study 1968, which included financial ratios and applied multiple discriminant analysis (MDA) for predicting the bankruptcy risk of corporate entities, whose literature has left a huge impression till this day (Altman, 1968). However, in modern studies logit model or the logistic regression model, probit model and neural network models are considered to be more superior in estimating the bankruptcy risk of the firms (Bellovary et al., 2007). However, I have chosen logit analysis for my study as the lowest model accuracy turns to be 20% and the highest accuracy tends to be 98%. From previous studies, it was known that the number of factors in a model varied from 1 to 57 factors (Bellovary et al., 2007). In our study we have taken 14 factors. The average number of factors applied in a model are ten as per previous studies (Bellovary et al., 2007).

This paper tries to highlight the following areas which were not addressed earlier.

1. To identify the number of companies lying in the distress zone.
2. To find the relationship between bankruptcy risk and various variables under study viz., market capitalization, price to earnings, price to book-value, level of working capital, retention level, operating profit margin, debt to equity level, total revenue and net worth of the companies.
3. To develop a bankruptcy prediction model for predicting the accuracy of the bankruptcy among the steel companies.
4. To find the major reasons behind the distressed condition of the steel companies.

The above study will thus help us to understand the level of bankruptcy in the Indian steel companies and thus will leave us with a scope to explore the current postulated model whether it fits similarly to other countries and industries as well. It also gives us a scope that to what extent the variables can be taken i.e., apart from the quantitative variables what other qualitative variables can affect the prediction accuracy of the model.

As per Achim et al. (2012) Principal component Analysis technique was used to assess the bankruptcy risk conditions in Romanian manufacturing companies. The study assessed the efficiency of the Romanian manufacturing companies and developing a model for gauging bankruptcy risks in two categories of companies i.e., good companies and bad companies. Again et al. (2014) were of the view that the company performance can be measured on any accounting-based metrics of financial performance represented by indicators like return on assets, return on equity, debt ratios, flexibility, etc. Similarly, various authors have found different results on the variables selected for the study (Kasgari et al., 2013).

Firm Size

As per the tenets of the agency theory, larger firms generally disclose more information to different users of the annual report which leads to a reduction in agency costs and thus reducing the level of agency risk. Previous studies have shown that the relationship between the firm size and the risk reporting of the firm is of mixed nature, for instance, (Beretta & Bozzolan, 2004; Hussainey et al., 2013) found a positive degree of relationship between firm size and levels of risk, (Hassan et al., 2006; Rajab & Handley-Schachler, 2009) found very low degree of relationship between the two variables. Here assume that large firms rely on finance from external sources; hence, they have incentives to disclose more risk information to send a good signal to investors and creditors about their ability to manage risk. In addition, large firms have sufficient resources to cover the cost of additional risk disclosures. Here, in our study, we have taken various measures to relate the firm size i.e., the market capitalization, total assets, the net sales and the net worth of the firm (Hernandez Tinoco et al., 2018).

Operating Profit Margin

Risk disclosure studies, reported a negative relationship between profitability and risk disclosure level, while (Hussainey et al., 2013) reported a positive relationship between these two variables. Nonetheless, agency theory expects that managers of companies with high operating profit margin would tend to provide more risk information in the interim reports, in order to justify their present performance to the shareholders.

Working Capital

According to signaling theory, companies’ managers will disclose more information if their liquidity ratios are high, to distinguish their skills in managing liquidity risks compared with other managers in companies with lower liquidity ratios. The current ratio is considered a true measure of the liquidity of the firm. The higher the ratio the better is considered the liquidity position of the firm. Marshall & Weetman (2002) & Hussainey et al. (2013) found that high-liquidity firms provide more risk information to send positive signals to investors (Qurriyani, 2013).

The Debt Level of the Firm

Based on tenants of agency theory, agency costs are higher in highly leveraged firms i.e., firms having a high debt to equity ratio. Generally, corporate managers in the retail industry tend to provide more risk management information in order to send a good signal to debt holders regarding the corporate ability to meet its obligations. Deumes & Knechel (2008); Hussainey et al. (2013); Hassan et al. (2006); Marshall & Weetman (2007); Taylor et al. (2010) found a positive relationship between the two variables, Abraham and Cox (2007), Linsley & Shrives (2006), and Rajab & Handley-Schachler (2009) found insignificant association between the two variables.

Price to Earnings (PE)

Price to earnings can be defined as market price per share divided by earnings per share. Sometimes used as a yardstick to benchmark and invest in the shares of the company. This can be sometimes misleading as well. Largay & Stickney (1980) highlighted that the in spite of the PE being double the organization went into bankruptcy. Hence, PE has a negative signal on the overall health of the firm. There is although a dilemma that PE may or may not vary with risk (Beaver & Morse, 1978).

Price to Book Value (P/BV)

Price to book value is measured in terms of market price per share divided by book value of assets a firm owns (Linsley & Shrives, 2005). The authors considered this measure because the historical return on equity is assumed to be a good indicator of future return on equity and also for the reason that the statistics required to estimate the relationship are simple (Wilcox, 1984). Furthermore, the book value of the assets is an indicator of the organic growth of the firm and hence, will be useful for predicting the bankruptcy of the firm (Linsley & Shrives, 2000).

Retention Ratio

The retention ratio is calculated as one minus the dividend payout ratio. In other words, the amount retained within the organization after the distribution of equity and preference dividend is divided by the total distributable profits of the firm (Investopedia, 2019). The more a company retains the more stable is the company in terms of the reserve. The level of retained earnings of a firm had a positive impact on the effect of the bankruptcy of any firm as it also envisages the changes in the profit structure in times of bankruptcy (Altman, 1968; 2014; William & Hansen., 1988; Libby et al., 1987).

Net Worth

Net worth can be defined as Total assets minus the long-term debt – current liabilities of the firm. Net worth is a strong indicator of the financial position of a business. Battiston et al. (2007) was of the view that the net worth of the firm becomes smaller when the firms are nearer to the verge of bankruptcy or under distress. Hence, net worth is considered to be a valuable measure for predicting bankruptcy (Xu & Zhang, 2009).

Total Assets

Total assets are used as a base for computing various useful ratios for predicting bankruptcy and used as a metric for measuring the organic growth of the firm (Elshandidy et al., 2013). Many studies have suggested that the firm’s total assets have a direct relationship with the bankruptcy condition of the firm. Bankrupt firms and firms in the distress zone have a poor return on assets and hence, poor organic growth. In our study, it is used as a useful barometer in predicting the bankruptcy of the Indian steel companies (Altman, 1968; 2014; Achim & Borlea, 2014; Elzahar & Hussainey, 2012; Bellovary et al., 2007; Hussainey et al., 2013).

Net Sales

Net sales are considered to be an important construct for the prediction of bankruptcy as the results of many studies suggest that the net sales of a firm plummet as they are on the verge of bankruptcy and negative profits also emerge from the same. Many studies were also of the opinion that sales and cash flows are the strong indicators of distress, they also send a strong signal to the investors about the performance of the firm (Bulow et al., 1978; Altman, 1968; Altman, 2014; Beaver, 1966; FlitzPatrick, 1932; Elzahar & Hussainey, 2012; & Bellovary et al., 2007).

So, after studying the results we implemented the logistic regression technique to predict bankruptcy and formulate the following hypotheses:

H_a1: Various variables like type of iron and steel companies, market capitalization, price to earnings, price to book value, level of working capital, retention level, operating margin, debt to equity level, total assets, net worth, sales, and CEO characteristics impact significantly the bankruptcy level of the selected Indian iron and steel companies in India.

H_a2: The distress level is more relevant in larger companies as compared to medium size and smaller companies.

Data and Methodology

Research Design

The study is exploratory as we tried to develop a model to predict the bankruptcy level of the steel companies. The study is descriptive in nature as well as we have used the various measures of central tendency i.e., the mean and the standard deviation to measure the efficiency of the model (Premachandra, 2011).

Sample, Sample Design

The sample under study is the steel companies who are operating in India. The source of the information regarding the size and the financial metrics are obtained from secondary sources i.e., from the annual report for the year 2015 of various steel companies. Judgmental sampling was done to go forward for the analysis. After administering 165 samples it was found out that 15 steel companies were having too many missing value cases which would be erroneous from our study (Ntim, 2011). So, with the remaining sample of 150, we proceeded toward our analysis. Again, for running and validating the experiment we dichotomized the dataset into test and training data sets. The training sample (n=125) companies comprised of 6 sponge iron and steel manufacturing steel companies, 10 large sized steel companies, 106 medium and small sized steel companies and 3 pig iron manufacturing steel companies. Even after the deletion of 15 steel companies, there were a few value cases that were then substituted by the mean value of each variable under the study. Similarly, the test sample (n=25) was composed of 6 large-sized steel companies, 18 medium and small-sized steel companies, and 1 pig iron company (Messier & Hansen, 1988).

Variables, Data Coding, and Model Design

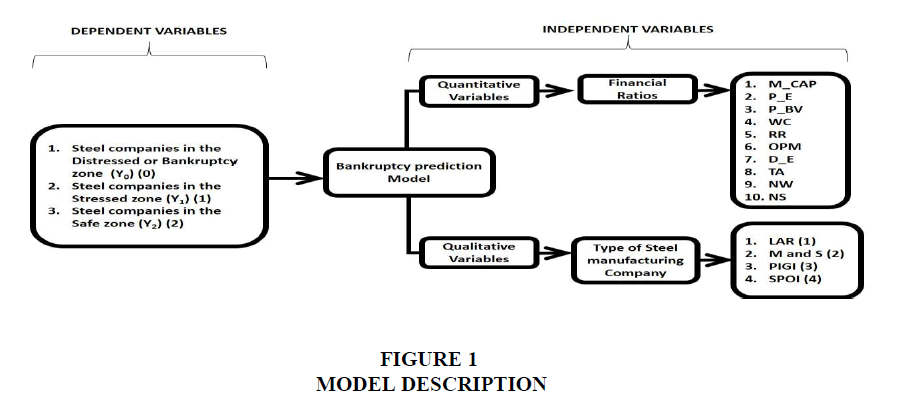
As stated earlier the study comprises secondary data collected and compiled from the annual reports of the various steel companies taken under the sample. The following Figure 1 shows the description of the qualitative and quantitative variables taken in our study. To assess the distress level of the companies we used the proxy of Altman z-score and computed the scores. Any score that was below 1.81 was considered to be in the distress zone, tagged as (Y0); scores between 1.81 and less than 3.0 were in the stress zone, labeled as (Y1) and any value greater than or equal to 3.0 was in the safe zone, coded as (Y2). The predictor variables are market capitalization (M_CAP), price to earnings (P_E), price to book-value(P_BV), level of working capital (measured by current ratio)(WC), retention level(RR), operating profit margin(OPM), debt to equity level(D_E), total assets(TA), total revenue (net sales)(NS), net worth(NW) and type of company, a four-level categorical variable viz. large size steel manufacturing companies (LAR) (1); medium and small sized steel companies (M and S) (2); pig iron manufacturing steel companies (PIGI) (3) and sponge iron manufacturing steel companies (SPOI) (4).

Figure 1: Model Description.

Statistical Tools

Altman Z-Score Model

The bankruptcy prediction model developed and prescribed by Altman (1968) which is as follows:

Z-score=0.012J1 +0.014J2+0.033J3+0.006J4+0.999J5(A)

Where, J1= working capital / total assets; J2 = retained earnings / total asset; J3= earnings before interest and taxes/ total assets; J4= market value of equity / book value of total liabilities; and J5= sales / total assets; and Z-score = the overall index.

Multinomial Logistic Regression

The multinomial logistic regression is also known as the polytomous logistic regression model is an augmentation of the binary logistic regression model also known as the binomial logistic regression model. This model is mainly used when there is an existence of more than two unordered or nominal categories in the study. Similar to the binary logistic regression the multinomial logistic regression analysis also uses the maximum likelihood estimation criteria to evaluate the probability of categorical association. The prediction model is formed with availability of n covariates and x constant as a vector of n+1 with a value x0=1 resulted into 2 Logit functions (Fagerland & Hosmer, 2012).

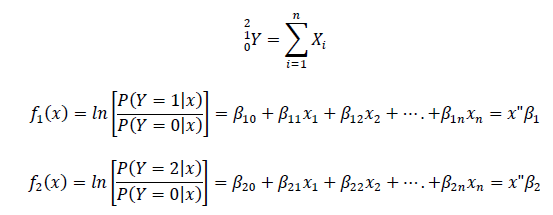(B)

Multinomial regression analysis is a multivariate technique that is mostly conducted after satisfying the normality conditions of the data, involving various input variables and output variables. Tabachnick et al. (2020) were of the view that usage of MLR technique has been:

1. It has a very robust to the violations of the assumptions of the multi-variate normality, equal variances, and covariance across the groups.
2. The output statistics can be interpreted easily.
3. MLR doesn’t assume a linear relationship between input and output variables.
4. The input variables need not be an interval
5. MLR also doesn’t make it mandatory that the input variables should be unbounded, and
6. Lastly, MLR does not assume the normally distributed error terms.

In regards to the above advantages, MLR is used a model-building tool to perform risk analysis and identification of risk factors for a given condition or a given risk profile (Madhu et al., 2014). Here the data was analyzed with the aid of both descriptive and inferential analysis (Vandemaele, 2009).

Findings

Descriptive Statistics

The descriptive statistics of the selected Indian iron and steel companies are given in the Table 1 showing that the average market capitalization (M_CAP), (M= 1041.1); standard error (SE= 364.76), standard deviation (SD= 3825.70) and Tolerance and variance inflation factor to detect multicollinearity problem, we found that (T= 0.72 and VIF= 1.39), which shows that multicollinearity is not an issue in our study. However, some variables like working capital do not meet the criteria (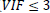), hence, dropped from our study. Similarly, other variables statistics are presented in Table 1.

Table 1 Descriptive Measures Showing – Mean, Standard Error, Standard Deviation, And Multicollinearity Measures
Variables	M	SE	SD	T	VIF
M_CAP	1041.14	364.76	3825.70	0.72	1.39
P_E	14.96	1.01	10.65	0.90	1.11
P_BV	1.22	0.16476	1.72	0.88	1.14
TA	4026.28	1278.43	13408.34	0.02	1.39
WC	-112.62	153.60	1611.01	0.23	4.35
RR	78.07	6.73	70.29	0.93	1.08
OPM	-6374.80	6333.99	65824.76	0.99	1.01
D_E	18.39	3.95	41.47	0.96	1.04
NS	1102.35	221.87	2327.02	0.68	1.47
PAT	-12.48	14.63	153.53	0.43	1.30
NW	1930.51	764.65	8019.80	0.72	1.39
ROA	-0.0537	0.21888	2.29	0.98	1.02
Note: M= Mean; SE= Standard error; SD = Standard deviation; T= Tolerance; VIF= variance inflation factor; market capitalization (M_CAP), price to earnings (P_E), price to book-value(P_BV), level of working capital (measured by current ratio) (WC), retention level (RR), operating profit margin (OPM), debt to equity level(D_E), total assets (TA), total revenue (net sales) (NS), net worth (NW) , return on assets (RoA).

Source: Author’s own compilation from IBM SPSS output.

Multinomial Regression Statistics

The statistics in the Likelihood Ratio Tests Table 2a and 2b. represent that variable like Market capitalization (M_CAP), Return on assets (RoA), Debt to equity (D/E), Net profit (PAT), Price to equity (P/E), and Price to book value (P/BV) ratios are having a significant effect in the proposed model.

Table 2a Likelihood Ratio Tests
Effect	Model Fitting Criteria			Likelihood Ratio Tests
Effect	AIC	BIC	-2 LL	X2	Df	p
Intercept	183.676	270.091	119.676a	0	0	0.000
Ln(Mcap)	192.163	273.177	132.163	12.487	2	0.002
Ln (ROA)	186.838	267.852	126.838	7.162	2	0.028
Ln(CA/CL)	182.055	263.069	122.055	2.379	2	0.304
ln (RR)	180.076	261.09	120.076	0.4	2	0.819
ln (D/E)	188.536	269.55	128.536	8.86	2	0.012
Ln (PAT)	191.654	272.668	131.654	11.978	2	0.003
Ln(NW)	182.553	263.567	122.553	2.877	2	0.237
Ln(P/E)	187.598	268.613	127.598	7.923	2	0.019
Ln(P/BV)	195.277	276.292	135.277	15.601	2	0
Ln (Sales / Total Assets)	182.596	263.611	122.596	2.921	2	0.232
Type of Steel Co	177.757	247.969	125.757	6.081	6	0.414
CEO Characteristics	181.893	257.507	125.893	6.218	4	0.183
Note: AIC = Akaike’s information criteria for the reduced model; BIC= Bayesian information criteria for the reduced model; LL= log-likelihood; = Chi-square value; Df= Degrees of freedom; p= probability values

Source: Compiled by authors from output of IBM SPSS®.

Table 2b Parameter Estimates
0=Bankrupt / 1=Stressed /2= Safe zonea		B	Wald	p	95% C.I.
0=Bankrupt / 1=Stressed /2= Safe zonea		B	Wald	p	LB
Steel companies in the Distressed or Bankruptcy zone	Intercept	-8	6.156	0
	Ln(Mcap)	1	4.442	0	1.05
	Ln (ROA)	-0	0	1	0.69
	Ln(CA/CL)	-0	0.37	1	0.45
	ln (RR)	-0	0.305	1	0.58
	ln (D/E)	1	3.838	0	1
	Ln (PAT)	-1	5.519	0	0.35
	Ln(NW)	-0	0.003	1	0.67
	Ln(P/E)	1	4.882	One or both parameter estimates are redundant.	1.17
	Ln(P/BV)	-2	10.83	0	0.07
	Ln (Sales / Total Assets)	-0	0.541	0	0.44
	Type of Steel Co=1	19	0	1	0
	Type of Steel Co=2	2	2.077	0	0.44
	Type of Steel Co=3	3	2.281	0	0.39
	Type of Steel Co=4	0c	0.000	0	0.00
	CEO Characteristics=1	0	0.058	1	0.21
	CEO Characteristics=2	-1	0.654	0	0.05
	CEO Characteristics=3	0c	0.000	0	0.00
Steel companies in the Stressed zone	Intercept	##	34.3	0
	Ln(Mcap)	-0	1.043	0	0.24
	Ln (ROA)	-1	4.162	0	0.35
	Ln(CA/CL)	1	1.059	0	0.61
	ln (RR)	-0	0.306	1	0.44
	ln (D/E)	-0	0.394	1	0.34
	Ln (PAT)	0	0.454	1	0.63
	Ln(NW)	1	2.057	0	0.8
	Ln(P/E)	0	0.006	1	0.19
	Ln(P/BV)	-2	5.063	0	0.04
	Ln (Sales / Total Assets)	0	0.254	1	0.58
	Type of Steel Co=1	31	0	1	0
	Type of Steel Co=2	17	0.000	0	###
	Type of Steel Co=3	0	0	1	0
	Type of Steel Co=4	0c	0.000	0	0.00
	CEO Characteristics=1	-0	0.02	1	0.1
	CEO Characteristics=2	-3	3.66	0	0
	CEO Characteristics=3	0c	0.00	0	0.00
Note: p= probability value; B= beta value; Exp(B)= Exponential Beta; C.I. = confidence interval for exponential beta; LB = Lower range; UB = Upper range. a. The reference category is: iron and steel companies in the safe zone. b. Floating point overflow. Its value is therefore set to system missing. c. Parameter is redundant.

For safe-zone companies relative to distressed companies, the Wald test statistic values against the associated p-value are given for the variables M_CAP, D_E, PAT and P_BV; who have a lower value than the level of significance at α= 0.05, and hence we failed to accept the H0, which signifies that the regression coefficient of the above predictor variables has been found statistically different from zero, for other given variables in the model. Similarly, for the other predictor variables, the associated p-value is greater than α= 0.05 and hence we failed to reject the H0. Which highlighted the fact that the regression coefficient of the above predictor variables has not been found statistically significant from zero, given other independent variables in the model.

The confusion matrix above demonstrates the correctly classified cases. The above model for train and training datasets exhibits the correct classifications in its diagonal cells. The key piece of information is the overall percentage in the lower right corner which shows that the resulted model (with all predictors & the constant) is 80.8% accurate Table 3 for the training dataset which narrates that the model fit is significant in the prediction of bankruptcy among steel companies. Almost similar results are also explored in the test sample (n=25) and it showed an accuracy of 80.0%. Hence, the accuracy of the model is quite justified and it is the researcher’s assumption that the model strength would further increase if the other qualitative and moderating variables are added to the outcome model.

Table 3 Confusion Matrix For Train And Test Samples Showing Prediction Accuracy
Train dataset (n=125)
Observed	Distressed or Bankruptcy zone	Stressed zone	Safe zone	Total	Percent Correct
Distressed or Bankruptcy zone	60	1	5	66	90.9%
Stressed zone	3	16	4	23	69.6%
Safe zone	7	1	25	36	69.4%
Total	70	21	34	125/125	(60+16+25)/125~80.8%
Test dataset (n=25)
Observed	Distressed or Bankruptcy zone	Stressed zone	Safe zone	Total	Percent Correct
Distressed or Bankruptcy zone	16	1	1	18	88.9%
Stressed zone	1	2	2	17	40.0%
Safe zone	0	0	2	27	100.0%
Total	17	3	5	25/25	(16+2+2)/25~80.0%

Source: Compiled by the authors from the output of IBM SPSS®.

To investigate the probability of default we computed the probabilities for both the test and the training datasets and found that 16.08% and 15.02% of the Indian iron and steel companies are safe, similarly, we also found that 12.93% and 13.42% of the iron and steel companies are in the stressed condition. Now to probe further into our main hypothesis (H1a) we found that approximately 71% and 71.56% of both datasets are on the verge of bankruptcy. This rises a concern to the iron and steel industry and the policymakers as the industry holds a significant contribution to the gross domestic product (GDP) of the economy. Another area of concern is the low profitability resulting in lower cash profits and rising debt levels which siphon off the cash flows of the Indian iron and steel companies. It was also found that equity owners are also somewhat responsible for the distress level of the Indian steel firms, which now leads us to answer our next hypothesis (H2a) that which type of firms are more in the verge of bankruptcy and financial distress. For addressing H2a, we tried to conduct the test of one-way ANOVA. So, firstly, we checked the assumption of the one-way ANOVA model and observed that out of total firms (n=150) who are large in size (n1=28); medium and small (n2=89) and sponge iron manufacturers (n3=7); a total of 124 firms under the level of distress and stress. After performing the multivariate normality test we found that there is a significant departure from normality, for large firms i.e., W(0.968)=27, p=0.01; medium and small firms i.e., W(0.465)=87, p=0.01; and for sponge iron manufacturing firms i.e., W(0.992)=6, p=0.01.We also checked for the outliers but did not find any outliers in the dataset. As a result of the above, we conducted the Kruskal-Wallis test, which detected that there are significant differences in the bankruptcy score (H (2) = 11.636, p=0.003) among the three categories of companies (large, small and medium, and SPOI). It was also discovered that, iron and steel companies which are very much vulnerable to closing down of operations are the sponge iron manufacturers (Mdn=-7.56); followed by medium and small sized iron and steel manufacturing firms (Mdn=-0.21) and lastly large firms (Mdn=0.82) Table 4.

Table 4 Probability Showing Indian Iron And Steel Companies In Safe Zone, In Stressed Zone And In Bankruptcy Zone Both In Training And Test Data Sets.
Probability of an Indian iron and steel companies being	Probability
	Training data	Test data
Safe	16.08%	15.02%
Stressed condition	12.93%	13.42%
On the verge of bankruptcy or in distress	71.00%	71.56%

Source: Own calculations compiled by authors.

Conclusion

This study thus gives us an insight that how qualitative variables like age of the company, board committee intensity, number of members in the committee of auditors; introduction of variables like synthetic credit rating may further improve the strength of the model. The study also gives us an overview that ancillary steel producing companies have low access to self-financed capital, thus most of the companies have to borrow huge amounts from financial institutions. This study can be used by practitioners in real-time to portend the bankruptcy of Indian iron and steel companies and thus, can come to the rescue from getting these companies into the distress zone. Secondly, the practitioners can use a strict regulation on the significant ratios that are identified in our model and thus can prevent the firm from going into liquidation. Policymakers can also prescribe threshold limits for maintaining certain key performance indicators like debt-to-equity ratio levels should be maintained between the ranges of 0.34 to 1.74. It can be implemented that any firm which is breaching this benchmark level of debt exposure will be dealt seriously or have to maintain a equivalent reserve fund to repay the debt amount. Similar benchmarks can also be also be set for liquidity, profitability and market capitalisation also. Thus, enabling the firms to be more sustainable and fit for survival in the long-run. To iterate further, investors could also apply this model to find and avoid investing in the companies which are at the verge of bankruptcy and thus will help them in selecting company stocks in near future. Similarly, other professionals like venture capitalists, banks, financial institutions, credit rating agencies can also implement this study to evaluate the Indian steel companies.

References

Abraham, S., & Cox, P. (2007). Analysing the determinants of narrative risk information in UK FTSE 100 annual reports. The British Accounting Review, 39(3), 227–248.

Academy of Accounting and Financial Studies Journal (Print ISSN: 1096-3685; Online ISSN: 1528-2635)

Predicting Bankruptcy of Selected Indian Steel Companies - A Multinomial Regression Approach

Abstract

Keywords

Introduction

Literature Review

Data and Methodology

Statistical Tools

Findings

Conclusion

References