Keywords

RMC (BPE in French), RMC Scheduling, RMC Distribution, PDPTW.

Introduction

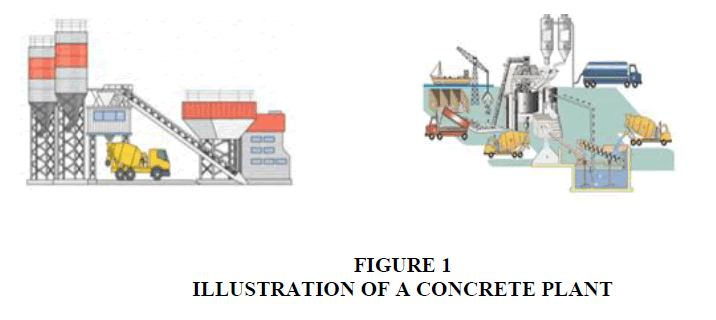
The production and distribution of ready-mixed concrete by a cement manufacturer Ready Mixed Concrete (RMC for short) plant and via concrete mixing plants (Centrale à Bétons or CAB for short in French) on construction sites are generally elaborated by experienced experts who capitalize on their accumulated experience and their feedback in addition to the advice and information collected from several stakeholders (the control office, the topographers, the soil study laboratory, the Scheduling-Planning-Control office Figure 1).

For construction sites, we are confronted with the problem of access and sometimes the inability to use traditional cement plants. In this case, we resort to concrete plants to produce cement on site.

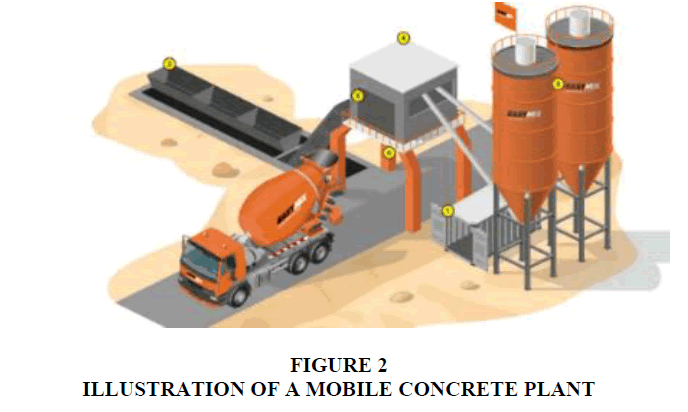
The concrete plant includes a control section, a batching plant with tanks dedicated to each input (G1 and G2 aggregates, for example, sand, cement, additives, water), mixers, a weighing system, a safety system Figure 2 ).

Positioning a primary or secondary base or a concrete production site (concrete plant + raw material warehouses, water tanks, fuel depot) requires the prior identification of all access roads (highways, roads, regional roads, tracks) with the calculation of distances. This task becomes complex in the presence of additional constraints related for example to the desert or uneven nature of terrain and requiring earthworks or bypasses. Other parameters must be considered such as the identification of potential suppliers and service providers, in particular the location of quarries for G1, G2, and sand, cement plants for bulk cement and admixtures delivered by full trucks, and even the water supply for certain sites.

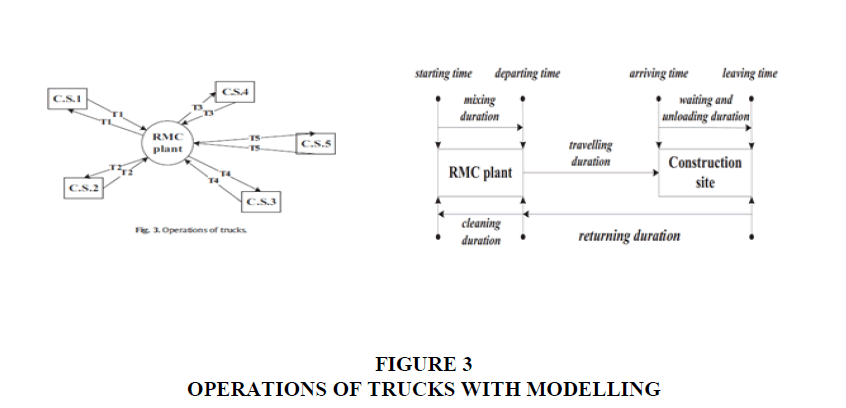
The identification of potential concrete production locations along the route is therefore a decision problem that may require general and/or ordinary earthworks. In addition to the costs, overheads, and delays involved in carrying out these earthworks, carrying out this type of work in difficult or hostile environments can impact the speed of the truck mixers (limited to a maximum of 30 Km/h) and consequently the journey times. This speed limitation, even for empty trips, will require us to move the CAB to several positions depending on the progress of the work and to readapt the traditional methods of management, monitoring, and control of the work. The truck mixers are characterized by a nominal capacity (8 m3, 10 m3, or 12 m3) and will perform concrete loading operations, loaded trips between the BAC and the delivered site, unloading operations, and empty trips between the delivered site and the BAC in addition to the cleaning operations of the mixers and possible waiting times. A truck router with a full load can visit a maximum of 2 neighboring sites for partial unloading operations. In the static case (in the absence of hazards), we assume that the router trucks are operational (no breakdowns, no absence of the driver, etc.) and available each morning with their drivers and fuel top-ups in the CAB queue Figure 3.

For Construction Sites in Large or Complex Projects, We Distinguish

• Fixed construction sites for which one or more concrete mixing plants (CAB) can be dedicated (e.g., construction of a dam or any other structure outside the range of action of cement plants)

• Mobile sites or sites spread over large distances (more than 100 km) for which one or more mobile concrete plants (mobile CAB) can be dedicated and moved to several production sites, considering operational constraints.

For a fixed construction site, we can use one or several fixed (stationary) and/or mobile concrete plants. For mobile sites, we generally use mobile plants. The stationary concrete mixing plants can have a capacity of up to 240 m³/h and the mobile versions have capacities ranging from 20 to 120 m3/h and a motor power of 30 to 130 KW depending on the model.

This mobility is relative since the concrete plants can be mounted on wheels or not. The plants on wheels have generally characterized a small production rate. The plants not mounted on wheels can have higher production rates but require the mobilization of heavy means for each movement.

Indeed, there are minimum requirements to move the CAB since specific cranes are needed (concerning the tonnage, the height of the boom), specific trucks, dismantling teams, assembly, adjustment, and testing teams to make the Mobile CAB operational after its displacement. Finally, earthworks and landscaping work to facilitate the loading operations of the truck mixers and the management of their lanes as well as to facilitate the maneuvers of the handling means and the trucks supplying the inputs.

The sites are spread out along a route with concrete demands to satisfy. These concrete requirements are calculated and estimated from the soil study and the calculations of the TSO (Technical Study Office). The demands can be readjusted or revised upwards during the acceptance of the excavations by the client, the design office, and/or the control office.

The transport orders associated with the delivery of concrete to the various sites are generally greater than the capacity of the truck mixers. The delivery of concrete by truck mixer must also be done within a limited time window to avoid the risk of the concrete setting even if we use admixtures (cement setting retarders).

Making the VBM work, is often a professional matter and requires a body of knowledge and know-how, especially concerning the coordination between production and distribution. Production is based on the prerequisites:

• The availability of human and material resources to operate the CAB while respecting safety conditions and HSE rules
• The availability of inputs and handling means to feed the tanks dedicated to inputs
• The availability of updated data and information necessary for production (re)planning and/or distribution re-scheduling
• The availability of routers and useful information on the progress of the trip.

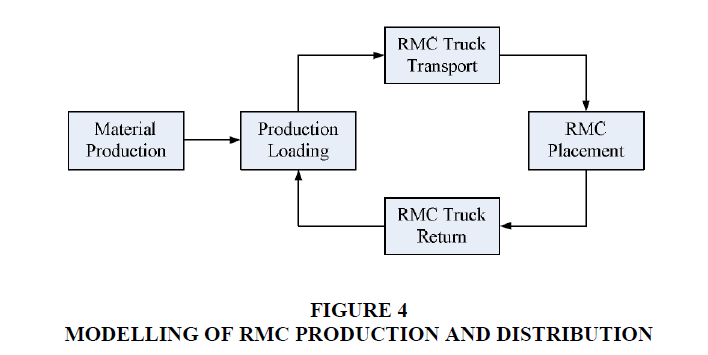
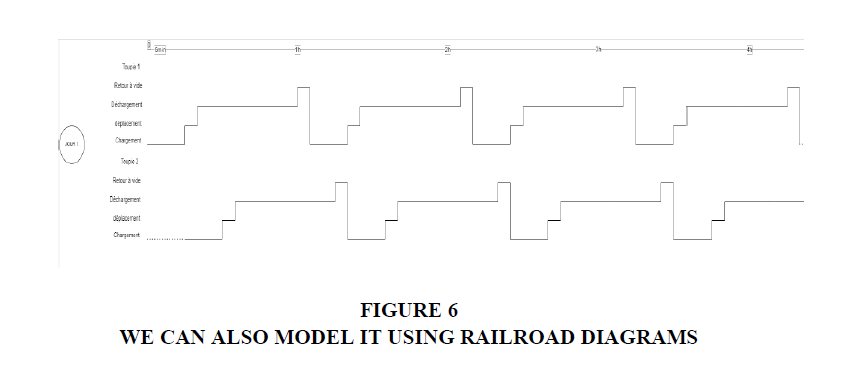
For the production of concrete, there are also minimum quantities to be produced to control the setup costs related to each production while allowing one or more partial stops in a shift. For example, at the beginning of the shift and according to the production schedule, operate the CAB for 1 hour and stop it for half an hour then launch the 2nd production of 1 hour then the 2nd stop of 1 hour Figure 4.

This will induce management rules in the planning of the rounds of the truck mixers and the synchronization of the loads. Moreover, it is necessary to produce only what will be consumed before the concrete sets, considering the loading times and the journey times. Depending on the type of concrete and the admixtures used (setting retarders), this duration can vary from 1 hour to 4 hours for the cases studied. This can be modeled with a constraint of maximum residence time (in the CAB+Truck mixer).

For the pouring of concrete, there is a great deal of coordination between the various parties involved to manage the administrative and contractual aspects (work coordinator, work manager, the client or his representative, or the laboratory that must be present, ...) and to manage the operational aspects (prior installation of metal formwork and reinforcement, availability of templates and setting tools, allocation of the necessary resources such as vibrators, concreting teams, ...). When all the prerequisites are met, a limited number of mixers can unload simultaneously because of the saturation of the zones and the lack of maneuverability on site (traffic and safety conditions in addition to the operating mode requiring the use of vibrators). In our case and since we are dealing with excavations, we only consider unloading by chute or via an extension of the chute (concrete chute). In practice and on other projects, the unloading can be done via a chute or pumps. Among the specificities of our project are:

Travel time is variable depending on the distance between the CAB location and the unloading site.

• All concrete pouring sites belong to the same project
• The casting sites can be managed by a subset
• There are time constraints in the CAB for each concrete pouring site
• There are constraints related to the quality assurance plan and follow-up
• There are workload smoothing constraints
• There are scheduling constraints for the truck mixer drivers, for the pouring teams, ... with the possibility of doing a limited number of overtime hours.
• The casting teams will move with their supplies and equipment from one casting site to another according to a schedule prepared and updated by the project manager and the work managers
• It is necessary to consider the concrete setting constraint which will require the CAB to be moved.
• The possibility for a full router to unload and distribute its full load on 2 neighboring pouring sites that meet the requirements of the pouring.
• It is necessary to find the right compromise between the displacements of the CAB and the cumulated times of driving loaded and empty.

We Have Treated 2 Cases (In The Study Phase):

• The non-preemptive case: if we start a pour, we must complete it in the same shift even if we have to use non-full trips. In this case, we use full and incomplete trucks (especially at the end of the shift). Moreover, some sites can be postponed to the next day if we are not sure to unload all the trucks in the allocated time.
• The non-preemptive case: if we start a pour with full trucks, we can finish it the next day using only full trucks. In this case, it is necessary to have concrete reinforcing bars and to use civil engineering techniques. The full truck will unload the rest of the concrete in a casting site and the rest of the load in another casting site.

Literature Review

Works related to the scheduling problems of the production and distribution of ready-mixed concrete are available in the literature.

Most of the consulted works of literature are interested in the management of the production, the management of the rounds either of a truck-mixer or a fleet of truck-mixers, for one or several cement factories or the production units of the GHP.

The production and distribution of ready-mixed concrete is a problem that has been characterized in the literature as a NP-hard problem (Yan et al., 2008). The presence of additional synchronization constraints is also NP-hard.

In his review of the literature, Yan et al. (2008) concludes the complexity and difficulty of solving vehicle routing problems with collections and deliveries and about the lack of attention in the literature to solving this type of problem as well as the youth of the research on this type of subject knowing that these problems are common in the industrial world and transportation services.

In his review of the literature on generalizations of Pickup and Delivery Problems with Time Windows (PDPTW) and related problems, Grimault (2016) focuses on the transportation of asphalt concrete in the public works sector, concrete delivery problems, industrial log truck scheduling problems (LTSP) and transportation problems with full trucks, transport problems with homogeneous fleets, transport problems with heterogeneous fleets.

The related problems are those problems in the literature that share a common base with the problems of concrete production and distribution.

The literature review Grimault (2016) of concrete transport problems shows the difficulty of the problem to be solved. Indeed, the planning must often be reconsidered, for an update of the order of a minute, according to the state of the concrete deliveries. Considering the size of the problems to be solved, the identified solvers are often limited by the computation time allocated to provide a solution of very good quality. Exact methods (mixed integer programming, constraint programming) are hardly applicable for industrial or large instances. The development of approximate methods such as Petri nets, flow simulation or heuristics, and meta-heuristics are recommended for large-scale problems. The complexity of the production and distribution of RMC is accentuated by the presence of synchronization constraints and implies the development of meta-heuristics for the resolution of industrial problems.

The literature review by Drexl (2012) proposes a classification for the synchronization required when more than one vehicle is needed for the completion of a transport task. In this classification, he distinguishes:

Task synchronizations define tasks that must be served once and only once by one or more vehicles.

Operation or movement synchronizations when the presence of a vehicle is necessary to move another vehicle.

Loading synchronization is when the sum of the loading and unloading flows of a product at a given point is equal to the demand of this point.

Resource synchronizations are defined when there is a limit to the simultaneous use of a resource at a given point by vehicles.

Ghasri et al. (2016) focus on concrete pouring conditions and the prediction of pouring conditions. The pouring time is generally considered from the time of arrival of the first router truck to the end of the unloading of the last router truck. The duration of concrete pouring does not only depend on the characteristics of the site since it depends on the supply process, the location of the site, and the traffic conditions, especially in cities with heavy traffic.

The production and distribution of concrete (Liu et al., 2014). And related problems (El Hachemi 2009; Durbin, 2003). can be modeled as a time-space network model with production and loading arcs, return arcs, and delivery arcs.

Methods and Resolution

Distribution policy is a decision-support problem that requires the development and testing of several strategies. Work is being done to develop such strategies and to develop heuristics and metaheuristics and flow simulations which will remain the subject of future dedicated publications (El Hachemi et al., 2015).

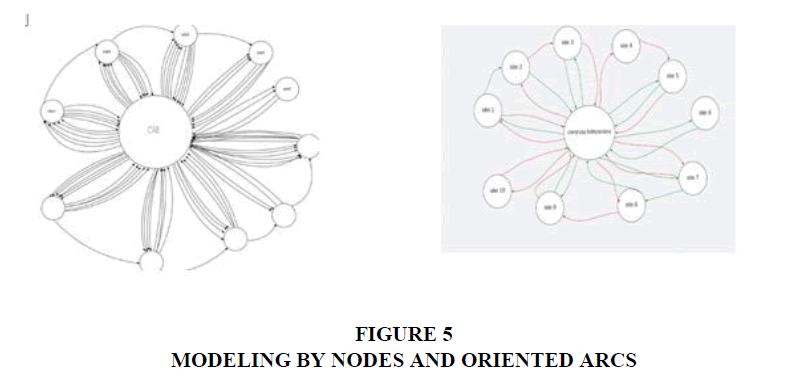
If we set a distribution policy, the problem c Figure 5 an be modeled and solved following different methods and formalisms listed in the scientific literature (Durbin, 2003; Durbin & Hoffman, 2008; Yan et al., 2008; Lin, et al., 2010; Masoud et al., 2016a; Masoud et al., 2016b). while adopting these works to our characterization of the problem. Indeed, the problem can be modeled in the form of diagrams with oriented nodes and arcs Figure 6.

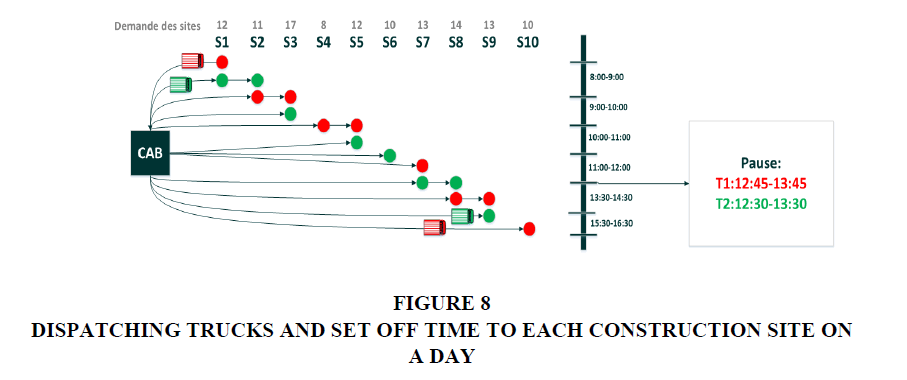
We can also use the truck router dispatching diagrams to determine the roadmap for each Truck mixer on a given horizon figure 7.

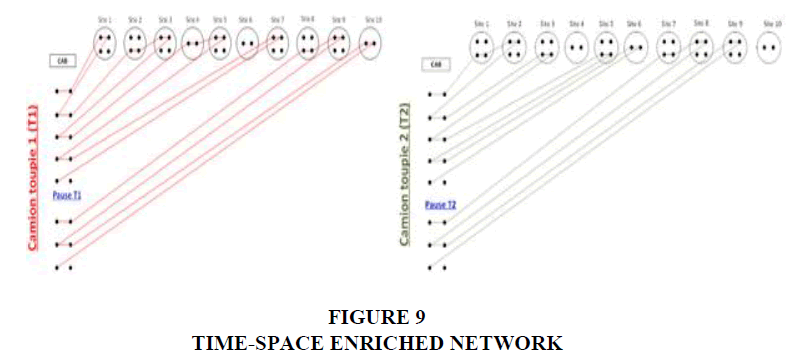
Finally, we can use a Network Arcs Formulation Model and its extension Enriched Network Model) for each truck mixer Figure 8.

For the industrial data of real construction projects, important preparatory work has been done to:

Obtain a real data set of more than 500 pouring sites with the needs in the earthwork, concreting, and various works Figure 9.

Obtain marked-out routes in the form of KMZ files with the location of the pouring sites and the identification of the ways (roads, regional roads, tracks) to carry out the calculation of the distances and the times of the travel according to the access ways.

As the data is confidential and to detail the working methodology, we are inspired by a real project to work on a fictitious data set while keeping similar orders of magnitude.

The fictitious project of our study is thus inspired by a large and complex project, carried out in a difficult and constrained environment, on a route of more than 250 km, requiring more than 12,000 m3 of concrete for 500 concrete casting sites with concrete demands ranging from 12 to 60 m3 per site and requires the planning of about 1200 trips if we consider a homogeneous fleet of 10 m3 mixers. It is necessary to manage and synchronize the flow of materials, information, work, etc., considering all the constraints of the project Table 1.

Table 1  Data From The Virtual Project
Concrete Pour Site	S1	S2	S3	S4	S5	S6	S7	…	S500
The Kilometre Marker	0	1	1.5	2	3	3.5	4	…	250
Concrete Demand In M3	11	11	15	15	11	10	12	…	45
Corrected Demand	12	11	17	16	12	10	15	…	50
Cumulative Corrected Demand	12	23	40	56	68	78	93	…	12400

In the figures, the CAB has a maximum capacity of 40 m³/h of concrete with a unit price of acquisition that exceeds 1,000,000.00 MAD. The displacements of the CAB can be modeled as a "setup time" with human and material resources needs and with a unit cost of 60,000.00 to 100,000.00 MAD for each displacement of the CAB and a delay between 2 to 4 days for its restarting and carry out the adjustments, tests, and earthworks.

We tested different time horizons (6 days, 2 weeks, 1 month) for planning and different time scales for scheduling operations (unit: 1 min, 5 min, 1 dht (10th hour or 6 min), 15 min, 20 min, 30 min, 1 hour).

The corrected demand is the demand after the reception of the excavation bottom which can generate additional earthworks. It corresponds to the concrete demand to be satisfied for each casting site.

The alignment can be curvilinear with uneven terrain with positive and negative slopes in addition to flat terrain. We consider the kilometer point to characterize the inter-site distances.

For the planning of the routing of the routers, we adopted the classical algorithms of Lot sizing to satisfy demand on a defined temporal horizon. These supply policies use the techniques of the lot sizing of the various classical algorithms namely lot for lot, economic period, economic quantity, Part Period Balancing, Silver-Meal, and Wagner Within.

Table 2 Tested Values Of The Quantity Ecq
ECQ tested	Justification of the CEQ value
8	For a homogeneous fleet of 8 m3 T. mixers
10	For a homogeneous fleet of 10 m3 T. mixers
16	For 8 m3 T. mixers operating in pairs
20	For 10 m3 T. mixers operating in pairs
18	For 8 m3 and 10 m3 T. mixers in pairs (heterogeneous fleet)
120	Daily quantity of concrete to be produced following an expert judgement
160	Daily quantity of concrete to be produced following an expert judgement
…	…

These policies allow comparing the performances to answer the question of what to produce and to meet which demand on which horizon Table 2.

These algorithms are adapted to our problematic; the calculation of the economic quantity ECQ for example takes into account the capacities of the routers and the operation of the CAB and the casting operations to propose values such as:

These batch sizing algorithms are coupled with a constructive heuristic that allows considering the location of the CAB, the travel times, and the loading and unloading times, ... to determine the load and the roadmap of each truck mixer.

Results

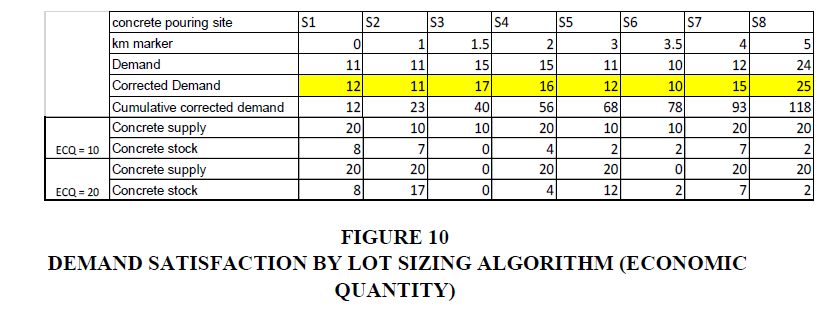
To illustrate the application of the lot-sizing algorithms, we restrict ourselves to 8 casting sites with economic quantities fixed at 10 and 20.

Figure 10 demonstrate the interest and the appropriateness of operating the displacement of the CAB, simulations were carried out with mixers of 10 m³ and allowed to have the following results (We solved using the Excel/VBA by rounding some numbers):

The loading and unloading times are fixed and assuming that the waiting times of the mixers will be negligible given the capacity of the CAB, we demonstrate the interest in moving the CAB. The gains in terms of time compared to the fixed daily costs largely offset the costs and time required to move the CAB with optimization and the best solution found is with 5 cabin moves, i.e., a 50 km step or a 25 km radius of action for the shredders Table 3.

Table 3 Calculation And Simulation Results
	2 Movements of the CAB	3 Movements of the CAB	4 Movements of the CAB	5 Movement of The CAB	6 Movement of The CAB
Cumulative distance traveled	55400	41750	32400	26500	24200
# of trips for mixers	1238	1240	1240	1235	1242
# of inter-site trips for mixers	573	570	578	574	571
Cumulative supply of concrete	12380	12400	12400	12350	12420
Cumulative Stock of concrete	2317	2308	2320	2337	2334
Transport time in hours at a speed of 30km/h	1847	1392	1080	884	807
Driving time in months (8h shift and 26d month)	8.87	6.69	5.19	4.25	3.88
Allowed times for CAB trips in J (worst case)	8	12	16	20	24
Allocated time in months	0.3	0.46	0.62	0.77	0.93
Cycle in months including transport with 2 T. mixers and CAB trips	4.735	3.805	3.215	2.89	2.87
Travel costs (worst case scenario)	200 KDhs	300 KDhs	400 KDhs	500 KDhs	600 KDhs

Discussions

In practice, we are confronted with the nature of the relief of the ground, the uneven grounds, the constraints related to the earthworks, and the access of the heavy machines, with the additional costs of the transport of the aggregates and raw materials, the follow-up quality, the reception, and the traceability. These constraints are going to impose us certain choices, less optimized for the placement of the CAB and displacements.

We were quickly confronted with the problem of balancing and smoothing the loads for different resources. Indeed, when we are close to the CAB, the number of sites that we can sink is important compared to its number when we move away, and the duration of full and empty transport becomes important compared to the duration of unloading. This imbalance causes problems in the field and makes some solutions unfeasible.To remedy this problem, we tested different delivery strategies that alternate delivery from remote casting sites and nearby sites by testing different casting site partitions.

Conclusions

We have succeeded in showing the interest of decision support methods to determine the locations and the number of trips of the CAB. If some locations are undergone or imposed by different constraints or configurations, we have demonstrated the interest of working on distribution strategies to optimize production and distribution while respecting all constraints.

At this stage, important preparatory work has been done to:

• Obtain real data of more than 500 casting sites with the needs in earthworks, concrete, and various works.
• Obtaining marked-out routes in the form of KMZ files with the location of the casting sites and the identification of the roads (roads, regional roads, tracks) to calculate the distances and travel times according to the access roads.
• Construct GANTT, railway diagrams, and RMC dispatching diagrams
• To develop a constructive solution that allows having an idea of the management of the construction site and the needs in resources and coordination/synchronizations.
• We plan to develop dedicated meta-heuristics and simulations for the production and distribution of concrete on a large construction project.

Finally, we would like to point out that the work carried out also has an environmental impact and improves road safety since it reduces the accumulation of kilometres travelled.

References

Drexl, M. (2012). Synchronization in vehicle routing—a survey of VRPs with multiple synchronization constraints.Transportation Science,46(3), 297-316.

Indexed at, Google Scholar, Cross Ref

Durbin, M.T. (2003).The dance of the thirty-ton trucks: demand dispatching in a dynamic environment. George Mason University.

Indexed at, Google Scholar, Cross Ref

Durbin, M., & Hoffman, K. (2008). Or practice-the dance of the thirty-ton trucks: dispatching and scheduling in a dynamic environment.Operations research,56(1), 3-19.

Indexed at, Google Scholar, Cross Ref

El Hachemi, N. (2009). Transport problem with time constraints. (Doctoral dissertation, Ecole Polytechnique de Montreal).

El Hachemi, N., El Hallaoui, I., Gendreau, M., & Rousseau, L.M. (2015). Flow-based integer linear programs to solve the weekly log-truck scheduling problem.Annals of Operations Research,232(1), 87-97.

Indexed at, Google Scholar, Cross Ref

Ghasri, M., Maghrebi, M., Rashidi, T.H., & Waller, S.T. (2016). Hazard-based model for concrete pouring duration using construction site and supply chain parameters.Automation in Construction,71, 283-293.

Indexed at, Google Scholar, Cross Ref

Grimault, A. (2016).Optimization of routes of trucks completed in the public works sector. (Doctoral dissertation, Ecole des Mines de Nantes).

Lin, P.C., Wang, J., Huang, S.H., & Wang, Y.T. (2010). Dispatching ready mixed concrete trucks under demand postponement and weight limit regulation.Automation in Construction,19(6), 798-807.

Indexed at, Google Scholar, Cross Ref

Liu, Z., Zhang, Y., & Li, M. (2014). Integrated scheduling of ready-mixed concrete production and delivery.Automation in Construction,48, 31-43.

Indexed at, Google Scholar, Cross Ref

Masoud, M., Lee, S., & Belkasim, S. (2016a). A heuristic approach for vehicle scheduling problem with time and capacity constraints. In2016 UKSim-AMSS 18th International Conference on Computer Modelling and Simulation (UKSim)(pp. 230-234). IEEE.

Indexed at, Google Scholar, Cross Ref

Masoud, M., Lee, S., & Belkasim, S. (2016b). A parallel approach for optimizing RMC delivery problem. In5th IEEE International Conference on Advanced Logistics and Transport, 1-3.

Google Scholar

Yan, S., Lai, W., & Chen, M. (2008). Production scheduling and truck dispatching of ready mixed concrete.Transportation Research Part E: Logistics and Transportation Review,44(1), 164-179.

Indexed at, Google Scholar, Cross Ref

Received: 26-Oct-2022, Manuscript No. JMIDS-22-12733; Editor assigned: 28-Oct-2022, Pre QC No. JMIDS-22-12733(PQ); Reviewed: 11-Nov-2022, QC No. JMIDS-22-12733; Revised: 15-Nov-2022, Manuscript No. JMIDS-22-12733(R); Published: 22-Nov-2022