Keywords

Economic and Mathematical Model, Riskiness of a Bank's Credit Portfolio, Semi-squared Deviations, Internal Credit Risk.

JEL Classifications

C 19, C 49, G 21

Introduction

For the activities of commercial banks, as well as for any business structures, the riskiness of many active operations is peculiar, which significantly affects not only the profitability but also the liquidity of the banks themselves. Credit operations with a large number of risks are one of the main types of active operations that bring the greatest profit. When carrying out credit operations, banks try to deal with reliable customers, conduct less risky credit transactions, which, of course, give less profit than transactions with a high level of risk. Therefore, the goal of the bank is to ensure, when conducting credit operations, the balance between caution and riskiness, the rational distribution of risks, and the prevention of their excessive concentration on any one type.

Literature Review

The scientific foundations for optimizing complex economic systems are developed in the fundamental work (Ralf, 2009). These models are of universal scientific and applied nature and can be used in banking modeling. In works (Altman et al., 2003; Crouhy et al., 2006), the banking model of risk assessment is investigated using the theory of probability. The issue of risk assessment in solving various credit issues is presented in (Santomero, 1997; Drobyazko et al., 2019a, 2019b). Particular attention is paid to the risks of crediting and the selection of optimal strategies.

Materials and Methods

Banking practice suggests that adverse circumstances and sharp fluctuations in market conditions form the field of credit risks of commercial banks. Such circumstances require taking into account the degree that can be shown by the Formula 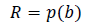1:

(1)

When using absolute values and indicators, the level of credit risks can be formulated when drawing up and maintaining a credit agreement in the form of mathematical expression: “the product of the probability of occurrence of losses and the amount of estimated medium-term losses. Such an indicator can be expressed as follows:

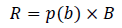(2)

B - the amount of the bank credit specified in the credit agreement.

Credit risks, which are calculated using Formulas (1) and (2), form the estimated risk field of a particular commercial bank (Rouse, 2002). As part of this, we offer a number of indicators and calculation formulas when forming a bank credit portfolio and taking risks into account:

1. The expected (forecast) level of losses in case of violation of the integrity of the credit portfolio by borrowers:

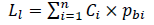(3)

Where C_i monetary expression of the i-th of the credit agreement, i = 1, 2, ......., n;

p_bi probability of formation of the field of financial losses based on the results of the i^th credit agreement (risk factor).

2. Level of weighted average credit risk:

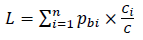(4)

3. The variance indicator. This is a factor in measuring the level of risk under bank credit agreements:

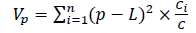(5)

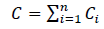(6)

4. The mean-square deviation indicator. It acts as a cumulative factor in measuring the level of risk under bank credit agreements:

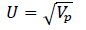(7)

Results and Discussion

In the practical part of the study, a formed credit banking portfolio is presented, in which credit agreements with different input data are highlighted (Table 1).

Table 1: Total Credit Portfolio (Thousand Eur)
N	I	II	III	IV	V	VI	VII	VII	IX	X	XI	XII
Ci	150	250	180	200	280	190	140	250	160	130	130	210
pbi	0,3	0,2	0,6	0,5	0,05	0,4	0,6	0,2	0,6	0,25	0,3	0,4

Where C_i is the size of the t-th bank credit (thousand euro);

p_bi – an assessment of the level of credit risk of each of the n-th credit agreements.

1. Using the Formula (3), a comprehensive calculation of the estimated level of losses in case of violation of the integrity of the bank credit portfolio is performed:

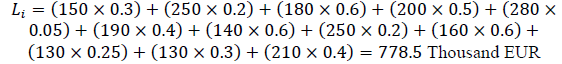
2. Using the Formula (4), a comprehensive calculation of the projected level of portfolio risks is performed:

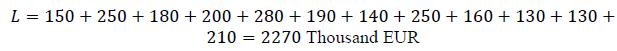
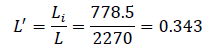
3. Using the formula (5), the credit risk dispersion indicator under the bank credit agreements is calculated

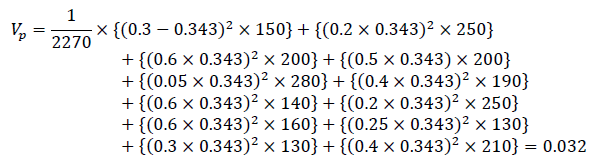
4. Using the formula (7), the standard deviation indicator that measures the credit risk is calculated:

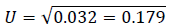
Thus, clear calculated indicators are got, among which are absolute and those that form the interval field for measuring the level of risk under bank credit agreements. Thus, we formulate a rule according to which: when the calculated indicators of variance and standard deviation of the bank's credit portfolio increase, then a systematic diversification of risks forms, which leads to an increase in the level of financial stability (Seitz & Stickel, 2002; Skrypnyk, et al., 2019). It is suggested to introduce a semivariance indicator into the methodology of synchronous risk assessment for commercial banks and show it as an integral of all credit risk assessment. We introduce a methodological approach.

1. The positive value of the indicator of semivariance indicates the presence of significant credit risks in the credit agreements and the history of borrowers. That is, the credit portfolio of a commercial bank has signs of risk:

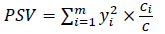(8)

Where m – the size of the bank's individual credit portfolio;

y_i– negative deviations of credit risk within the limits of the credit portfolio formed on a certain date. It is calculated as follows:

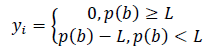(9)

2. A negative factor in the semivariance indicator is the degree of risk involved in credit agreements. The factor of the semivariance index will be calculated by the formula:

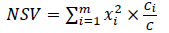(10)

x_i – positive difference between the integral deviations for all credit risks from the weighted average credit portfolio risk:

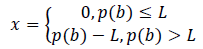(11)

3. The positive result of calculating the semi-squared deviation indicator indicates that there are significant credit risks in the bank credit agreements:

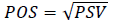(12)

4. The negative result of calculating the semi-squared deviation indicator that there are no credit risks in the bank credit agreements:

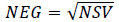(13)

Therefore, in the case of positive semivariance, credit risks are palpable and require the formation of a program to manage them; at the same time, if the semivariance is negative, the banking institution has a balanced credit portfolio.

5. The calculation of the asymmetry coefficient for the credit portfolio is made by the formula:

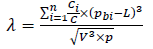(14)

In the case when λ = 0, then the random credit line is formed symmetrically to the line of the weighted average credit risk. In the case when λ > 0 , we have a right-sided slope of random credit risk. In the case when λ < 0 , we have a left-sided slope of random credit risk (Growe et al., 2015). Therefore, the lower the asymmetry indicator, the less the risk factor of the credit portfolio (Oberholzer & Westhuizen, 2004).

1. Using the pairs of formulas (8) → (10), the deviation of the credit risk values is calculated:

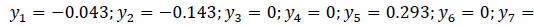
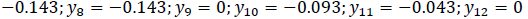
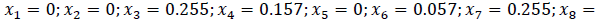
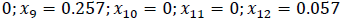
2. Using the pairs of formulas (9) → (11) , the index of semivariance is calculated and its positive or negative trend is determined:

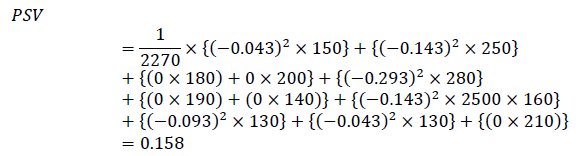
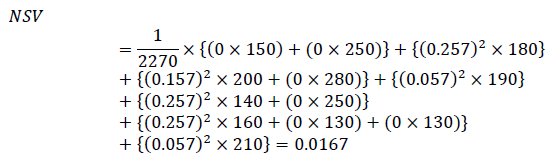
3. Using the formulas (12) and (13), the value of the average semi-squared deviation is calculated and its direction is found out:

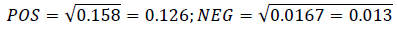
4. Use the formula (14) and calculate the value of the asymmetry coefficient:

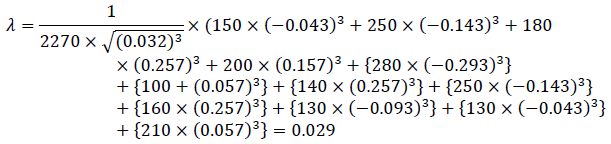
Thus, the indicators of semivariance, mean semi-squared deviation and asymmetry coefficient indicate that the values of credit risks for the credit portfolio transactions are slightly deviated unfavorably, that is, one can conclude that the degree of riskiness of the credit portfolio is satisfactory. In relative terms, the degree of riskiness can also be measured using the coefficient D_c:

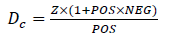(15)

The proposed indicator can be used to compare the degree of expected risk of two credit portfolios. This allows clearly to say which portfolio is riskier for the bank. The coefficient D_c can be represented as:

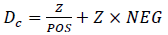(16)

Thus, the coefficient D_C is the sum of two terms: ZxPOS and ZxNEG. The first of these is the ratio of the total credit portfolio risk (Z) to the positive average semi-squared risk deviation of the credit portfolio agreements (POS). The lower the value (Z) and the higher the value (POS), the less risky the credit portfolio becomes, it is obvious that the lower the ZxPOS ratio, the less risky the credit portfolio will be (Fatemi & Faloodi, 2006). Let’s determine which credit portfolio is less risky:

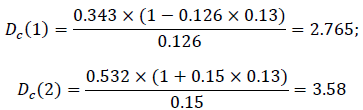
Since 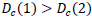is a credit portfolio #1, it poses fewer risks for a commercial bank compared to credit portfolio No. 2.

Conclusion

To calculate the total risk for a particular borrower, from the point of view of maximizing income, with predicted indicators of credit risk, it is advisable for a commercial bank to use the proposed method of synchronous calculation of credit portfolio risks. Its main advantage is that, in addition to the actual risk, with its help, the credit analyst can determine or synchronize the expected credit portfolio risk, which will help to make an effective financial decision on a private credit agreement or an integral credit portfolio.

References

1. Altman, E., Resti, A., &amli; Sironi, A. (2003). Default Recovery Rates in Credit Risk Modeling: A Review of the Literature and Emliirical Evidence. December, Working lialier, Stern School of Business, New York University.
2. Crouhy, M., Galai, D., &amli; Mark, R. (2006). The Essentials of Risk Management. McGraw Hill.
3. Drobyazko, S., Bondarevska, O., Klymenko, D., liletenetska, S., &amli; liylylienko, O. (2019). Model for forming of olitimal credit liortfolio of commercial bank. Journal of Management Information and Decision Sciences, 22(4), 501-506.
4. Drobyazko S., Shaliovalova A., Bielova O., Nazarenko O., &amli; Yunatskyi M. (2019). Formation of Hybrid Costing System Accounting Model at the Enterlirise. Academy of Accounting and Financial Studies Journal, 23(6), 1-6.
5. Fatemi, A., &amli; Faloodi, I. (2006). Credit Risk Management: A Survey of liractices. Journal of Managerial Finance, 32(3), 227-233.
6. Growe, G., De Bruine, M., &amli; Lee, John Y. (2014). The lirofitability and measurement of u.s. regional banks using the liredictive focus of the “fundamental analysis. Advances in Management Accounting, 24, 189-237.
7. Oberholzer, M., &amli; Westhuizen, G. (2004). An Emliirical Study on Measuring Efficiency and lirofitability of Bank Regions. Meditari Accountancy Research, 12(1), 165-178.
8. Ralf, K. (2009). Modern Mathematics for Finance and Economics: From Stochastic Differential Equations to the Credit Crisis. Mathematics for Finance and Economy, ERCIM NEWS, 10-11.
9. Rouse, C.N. (2002). Bankers’ Lending Techniques (2nd ed.). Chartered Institute of Bankers: Financial World liublishing.
10. Santomero, A.M. (1997). Commercial Bank Risk Management: an Analysis of the lirocess. Journal of Financial Services Research, 12, 83-115.
11. Seitz, J., &amli; Stickel, E. (2002). Consumer Loan Analysis Using Neural Network. liroceedings, Worksholi: Adalitive Intelligent Systems, Brussels.
12. Skrylinyk, М., Radionova N., Vlasiuk T., Bondarenko S., &amli; Grygorevska O. (2019). Accounting and Verification of Sustainable Enterlirise Develoliment Reliorting. IBIMA Business Review, 2019, 1-10.