Keywords

Decision Modeling, Decision Sciences, Real-world Problems, PISA

Introduction

In developing countries, modeling real situations is a requirement during the fourth industrial revolution. According to Islam et al. (2018), the absence of practical research and technology application is a major obstacle for developing countries like Bangladesh or Vietnam that can adapt in the context of the knowledge economy. Hence, modeling real-world situations is a way to be concerned in developing countries. Therefore, which model and how should sustainability be modeled in society?

According to Chang et al. (2017), the development of linked theoretical models in the fields of information management, decision science and financial economics is a promising development. These models can also be strengthened through teaching students at high schools to shape future generations of citizens serving the 4.0 industrial age. It is possible to build many models for teaching; however popular models, which are widely used, can be mentioned as decision models in Mathematics, STEMTech models for Natural Sciences subjects (Tuan et al., 2019a), etc.

Decision modeling is derived from the idea of Realistic Mathematics Education (RME), a theory of teaching and learning Practical Mathematics comes from the Netherlands. According to Freudenthal (1968), Mathematics educators have brought up numerous problems related to modeling by asking questions "Why to teach Mathematics so as to be useful? Why can't several students utilize Mathematics knowledge learned to solve real problems even though they have achieved excellent certification in this subject? Mathematics is taught so that students can apply Mathematics to simple situations of life". In the middle 1970s, Decision modeling is still continued to be mentioned by Ang (2001), Deutschland et al. (2004), Blum et al. (2007), Aris (2012), Bourne (2018), Burger et al. (2018), Caccavo et al. (2018), Shorten et al. (2018), Gazi (2019), Khan et al. (2019), Mahmoudi et al. (2019), Pho et al. (2019a, b, c) and Tuan et al. (2019b), etc.

The relationship between Mathematics and Modeling is more developed when this issue is discussed at the conference held in Germany in 1977, including discussions on aspects of applied Mathematics in education. Blum & Niss (1991) affirmed the knowledge approach by modeling the studying of Mathematics to become more meaningful, motivating and passionate about learning Mathematics.

Several countries on over the world have updated the modeling trend and achieved positive effects in teaching and learning Mathematics and developing problem solving capacity for learners. Trends in Decision modeling into programs and textbooks to other levels are one of the compulsory competencies of the national standard of education in Mathematics. Specifically, American textbooks are mentioned to numerous practical problems in each lesson and chapter. Calculus is a set of Mathematical calculus syllabus written by Canadian Mathematician- James Stewart that connects the basic theory of Mathematics in the fields of natural sciences, social sciences and the practical issues of life, creating attraction for learners. In Singapore the application of RME theory and Decision modeling has brought about very good results in teaching at high schools. Developed countries have implemented Mathematics learning to be linked to the reality of high school teaching programs at all educational levels thus students know how to apply knowledge from classroom lessons into practice. International Conferences on the Teaching of Decision modeling and Applications (ICTMA) is organized every 2 years with the aim of promoting application and modeling in all areas of Mathematics education. In addition, several practical Modeling problems have been included in the 15-year-old student performance assessment called the Programme for International Student Assessment (PISA) has been established by the Organization for Economic Cooperation and Development (OECD) since 2000. The PISA program is now very successful, attracting great attention of numerous countries in the world: until 2015, there are 65 countries around the world have registered for evaluation under this program, of which Vietnam ranked 12/65 participating countries.

In Vietnam, President Chi Minh Ho suggested that education should be attached to practice, and thus, he has instructed the younger generations to follow the motto "Learning to go together with practice” in their study (Thu, 2017). Learning to think, to relate with reality, to have experiments and practice. Learning and practice must be combined". With this thought, the association of Mathematics content in books with several practical situations in real life is a good idea and meaningful in teaching. The Ministry of Education and Training in 2016 has clearly defined the education reform orientation as "Developing teaching topics in each subject and interdisciplinary topics, strengthening activities to help students apply interdisciplinary knowledge to solving numerous practical problems". In addition, Nguyen (2015) is one of the leaders in receiving Decision modeling trends with several articles. Furthermore, Le (2014) affirmed that "Mathematics originates from practice, and every Mathematical theory, though abstract, finds its application in practice."

It can be seen that, putting practical Mathematics into teaching at high schools is extremely necessary and consistent with the requirements of developing education. Nevertheless, there are not numerous problems with practical factors in Mathematics and textbooks for students to apply knowledge to solve. Specifically, there is no problem in modeling in the 12^th grade textbook; the analytical part has a few problems that have been introduced but not diverse in quantity and quality assurance. Hence, it is extremely meaningful for us to conduct research to build two geometry problems in the 12^th grade Mathematics program called "cylindrical glass house" and "find the location of machines to catch bird Nest".

The rest of the paper is structured as follows. We review of the programme for International Student Assessment (PISA), perspectives on Decision modeling, teaching by modeling and process of developing modeling problems from practice in Section 2. Section 3 describes about the practical situation in Vietnam and methodology. Discussing about the empirical analysis is presented in Section 4. Concluding remarks and inference will be provided in the last section.

Literature Review

The Programme for International Student Assessment (PISA)

The Programme for International Student Assessment (PISA) was developed and coordinated by the Organization for Economic Co-operation and Development (OECD) in the late 1990s and is now receiving the attention of numerous countries on over the world. This organization only specializes in assessing the universal capacity of students aged 15 with global scale, not only mentioning Decision modeling but also focusing on this issue. Specifically, the application of Mathematical knowledge to solve practical problems is ranked and level 3 of the assessment scale and Modeling skills are highly regarded.

Typical types of questions and problems of PISA

Types of questions and problems of PISA are mainly in the following 7 types of Mathematics including:

1) Approximation and relativity
2) Tables, charts and graphs
3) Motion Mathematics
4) Problem with open questions
5) New formulas and expressions
6) Mathematics inference
7) New concept

Some notes when solving PISA problems

(i) Must know to look at "Excess hypothesis"

The problems of PISA often have the instructions given in words, drawings, images, tables, graphs, etc. and then some questions. So, if students do not understand exactly what hypothesis is necessary and important, they will be very difficult and time consuming to find the solution of problem.

(ii) Must know to fully exploit "Lack of hypothesis"

Practical situations are quite diverse and hypothesis problems do not always provide sufficient information to solve these issues. Students must rely on knowledge from practice and their knowledge to find more information.

(iii) Must be familiar with approximation and relativity

Practically most utilize the approximation of values and the relativity of results. Thus, when solving numerous practical problems, students need to know the approximation of values to the calculated results must be consistent with reality.

(iv) Must be familiar with other expressions, formulas and knowledge with knowledge in schools

When dealing with several practical situations, students must know more about daily life and still be in the basic knowledge that students are known from family and society. Through these forms of Mathematics, students will gain more interdisciplinary knowledge and knowledge from social life.

(v) Must be familiar with the requirements of open questions

Based on practical analysis, PISA problems require numerous skills such as inference, analysis, synthesis, self-understanding, etc. PISA's open questions will help students expand their knowledge and improve in practical knowledge.

Perspectives on Decision Modeling

Nguyen (2012) mentioned that "Decision modeling is the process of converting the practical problem to Mathematics problem by setting up and solving Decision modeling, demonstrating and evaluating solutions in real context, improving models if solutions are not acceptable. Nguyen (2015) presented the concept of Modeling in teaching Mathematics as a process of discovering and solving practical situations with the tools of Mathematics and support of information technology, thereby training for students. Generating thinking skills and manipulating mathematics such as analysis, synthesis, comparison, generalization, abstraction. Based on Mathematics languages such as symbols, graphs, diagrams, formulas, equations, students grasp the relationship between phenomena in nature and society with the content of knowledge Mathematics in textbooks. According to Le (2014), Decision modeling is the process of refining and refactoring the key points of a practical problem by tasks such as hypothesis, generalization, formalization, etc. to create honest Mathematical problems with real situations.

Thus, it can be seen that Decision modeling is utilized to understand and solve practical problems as a tool for teaching and learning mathematics in high school, is an environment for students to learn and explore the relationship between knowledge of Mathematics, other interdisciplinary knowledge and practical issues.

Teaching by Modeling

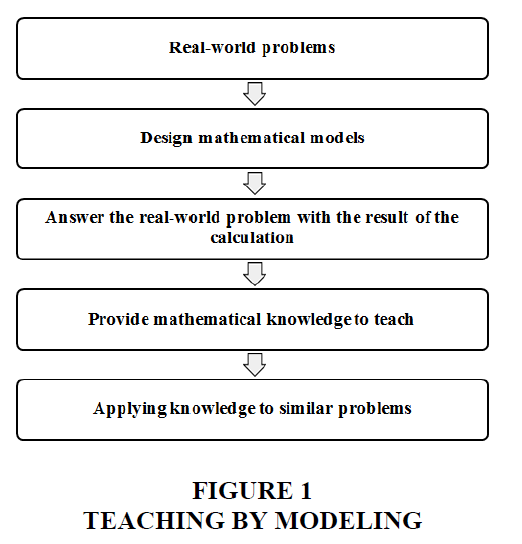
Mathematics Teaching can be done in two opposite processes: putting the knowledge first and solving the problem, or conversely putting the problem then forming knowledge. This issue can be illustrated as in Figure 1.

Thus, Teaching by Modeling is to bring the Modeling problem for students to solve under the guidance of teachers, thereby forming knowledge for students to apply to similar Mathematical forms. The result of the research process to solve practical problems is the knowledge of Mathematics that students need to study. Moreover, Teaching by Modeling allows overcoming the disadvantages of traditional teaching methods because students grasp new knowledge through practical situations, thereby learning how to perceive situations and then find solutions to other similar situations.

Process of Developing Modeling Problems from Practice

Kendall (2011) introduced a book with the title "Understanding common core state standards". The author suggested that a basic cycle of Modeling can be done in 6 steps:

1) The problem is derived from practical situations, recognizes variables in the situation and chooses variables that show the necessary features.
2) Formulate the model by creating and selecting geometric representations, graphs, tables, algebra or statistics to represent the relationship between variables.
3) Analyze and perform calculations on those relationships to draw conclusions
4) Interpret the Mathematics results according to the original situation
5) Validate results by comparing them with situations, then improving models (return to step 2)
6) If the results are accepted, write a conclusion report.

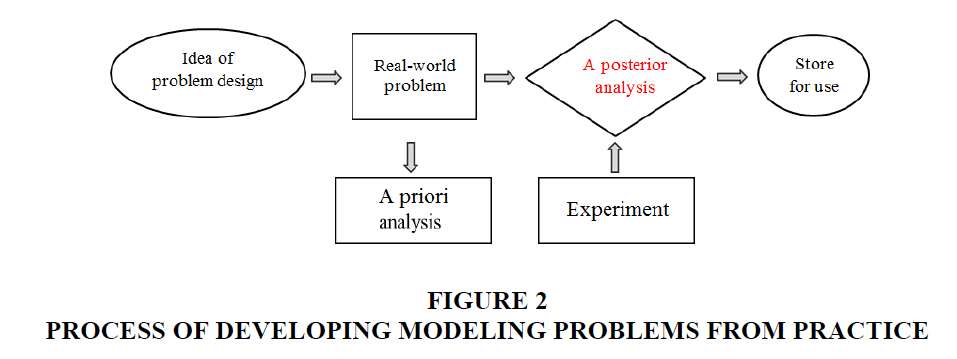
Throughout this cycle, there are always choices, assumptions, and approximations. The Common Core State Standards Modeling cycle is a closed process that begins with practical issues and then returns to solving those problems. This proves that if we solve the problem modeling from practice, it will also solve the initial problems. This is an extremely important meaning of the results of modeling problems. From the idea of Common Core State Standards, Tuan & Luan (2014) proposed the process of developing practical problems with 6 steps is described as in Figure 2.

1) Analysis of program content and idea of problem design
2) Develop Mathematics problems and solutions (can redesign the problem in the form of learning slips)
3) A prior analysis
4) Experiment on groups of at least 30 students
5) A posterior analysis, compare experimental results with empirical results to improve the problem, then repeat the process from step 2, or if accept the improved problem then switch to step 6
6) Store for use.

In this paper, we select the process of developing practical problems according to process of Tuan & Luan (2014) to build two geometry problems.

The Practical Situation In Vietnam And Methodology

The Practical Situation in Vietnam

Because the 12^th grade Mathematics textbooks program in Vietnam is unique in all the country. For the purpose of understanding and analyzing this issue, we have approached the time frame of the 12^th grade Mathematics textbooks program at Luu Huu Phuoc high school. The 12^th grade Mathematics textbooks program is described in Table 1.

Table 1:The 12th Grade Mathematics Textbooks Program
	All year		Semester 1		Semester 2
	Quantity	Percentage	Quantity	Percentage	Quantity	Percentage
Analytics	94	63.51%	48	63.16%	46	63.89%
Geometry	54	36.49%	28	36.84%	26	36.11%
Total	148	100%	76	100%	72	100%

According to the above statistics, one found that the number of lesson about Analytics in both semester I, II and the whole year was dominant compared to the number of lesson about Geometry (compared to 1.5 times higher). The specific chapters in the program are illustrated in Table 2.

Table 2: The Specific Chapters In The Program
Analytics
Chapter	Name of chapter	Number of lessons
1	The application of the derivative to survey and graph function	22
2	Power, exponential and logarithmic function	22
3	Primitives, integral and application	16
4	Complex numbers	10
Geometry
Chapter	Name of chapter	Number of lessons
1	Polyhedra and their volume	12
2	Sphere, cylinder, cone	10
3	Method of coordinates in space	17

Thus, for chapter "Sphere, cylinder, cone" and "Method of coordinates in space" accounting for nearly 70% of the lesson of geometry and 25% of the whole school year. These data demonstrate that knowledge in these two chapters accounts for a relatively high amount of the 12^th grade Mathematics textbooks program. In addition, we also provide about statistics of the number of problems mentioned in the 12^th grade Mathematics textbooks program is presented in Table 3.

Table 3: The Number Of Problems Mentioned In The 12th Grade Mathematics Textbooks Program
Name of chapter	Number of lessons
The application of the derivative to survey and graph function	8
Power, exponential and logarithmic function	8
Primitives, integral and application	5
Complex numbers	0
Polyhedra and their volume	0
Sphere, cylinder, cone	0
Method of coordinates in space	0
To test illustrates 1st	4/50 question
To test illustrates 2nd	3/50 question

Thus, it can be seen that there are 22 practical problems in a total of a lot of the 12^th - grade Mathematics textbooks exercises but account for nearly 10% in the subjects illustrating the National High School exam. This data provides a view that the number of exercises and examples of practical Mathematics in textbooks do not meet the learning needs of students, test teachers' assessments and catch up with the development orientation capacity to solve problems that the Ministry of Education has instructed. In addition, in the exam, the form of geometry in practical mathematics appears but the textbook does not exist any problem in the field of geometry. This is the drawback we want to add.

Analysis of the Practical Situation in Vietnam

The Modeling problems mentioned in textbooks have the following positive aspects: Present some of the necessary forms of Mathematics for life in learning such as Mathematics about interest rate, maximum and minimum value (saving production costs), with interdisciplinary factors with Biology, Physics, Chemistry and practical situations. Furthermore, Mathematics problems with instructions or detailed explanations help students learn better. Besides, the first step is to confirm the necessary role of the problem Modeling reality in students' thinking, helping students understand part of the application of knowledge learned in life, answering the question "Learning for what?".

Nevertheless, Modeling problems in textbooks still have the following limitations: Mathematics forms often focus on one topic, so they are not diverse and abundant (focuses on the form of maximum and minimum value, the form of interest rate, and the remaining forms almost do not have). Compared to the number of lesson in program distribution, the number of modeling problems from practice is very small. The problems are still heavy on Mathematics, not really close to real life, and the application is not high. The problems have not yet been trained for high school students to solve problems from real life, not yet drastically in improving the ability to apply the knowledge learned as expected, not really causing interest in learning for students. In addition, the geometry has no practical problems.

The biggest drawback of modeling problems in the 12^th grade Mathematics textbooks is that it has not been included in the program to study geometry problems, although the application of geometry problems is extremely diverse and abundant. Thus we propose two geometry problems in the next subsection.

Methodology

To help students better understand the relationship between geometric knowledge and practice, the problems also promote interdisciplinary factors and are consistent with the orientation of PISA. We propose two geometry problems "cylindrical glass house" and "find the location of machines to catch bird Nest" to create excitement and enhance the ability to solve problems according to Mathematics Modeling. Because in the 12^th grade Mathematics textbooks program, when the number of Analytics modeling problems accounts for a large number that is included in the curriculum, the geometry does not have a lesson. Therefore, we conducted the design of two geometry modeling problems to complement the limitations of textbooks, connecting the knowledge of mathematics and the diversity and originality of practice. The idea of designing two issues comes from real problems in life.

Problem about "cylindrical glass house"

With the diversity of geometry in practice, cylinders appear most of things around us such as soft drink cans, potato cake boxes, milk boxes, etc. in particular, houses with cylindrical shapes. Problem "cylindrical glass house" helps students better understand the knowledge of chapter "sphere, cylinder, cone", and combined with construction knowledge. With the present era the trend of "Decision modeling" architectures is widespread and prevalent. Readers may refer in Torregrosa et al. (2012), Prescott (2013), Cao & Barrionuevo (2015), etc. Therefore problem "cylindrical glass house" is a highly applicable and typical problem thus we study it in this section.

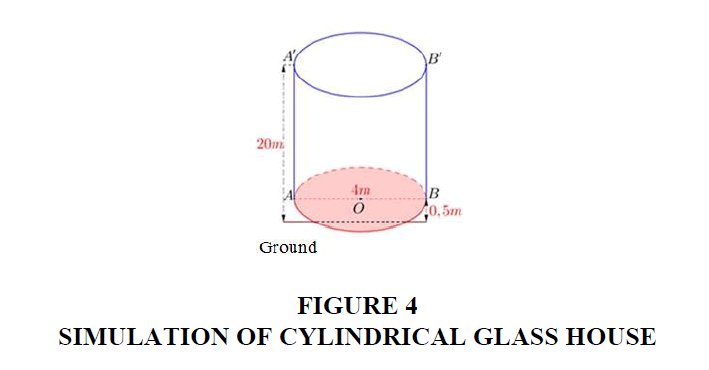
The cylindrical glass house is an extremely interesting idea when allowing people in the house to see the scenery around 360 degrees. The cylindrical-shaped house is surrounded by the wall with the design of the upper surface of the cylinder is fitted with a glass, while the bottom surface of the cylinder is not fitted with glass. This house is designed 0.5 m above the ground, its height is 20 m above the ground, the bottom diameter is 4 m. Calculate the amount to use (unit of USD) to buy glass for surrounding walls and the upper surface of the house. Assuming the price of tempered glass is 35 USD/m2. This house is illustrated as in Figure 3.

To solve this issue, it is necessary to draw the picture again. Figure 4 can be redrawn as follows:

Considering cylindrical shape with two bottoms are circle O center and diameter AB = 4m, height AA' = 20m.

It can be observed that

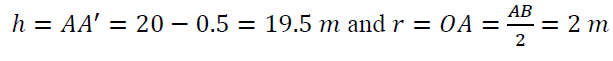
The surrounding area of the cylinder is

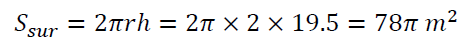
The upper surface area of the cylinder is

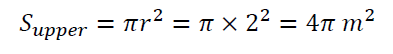
The area to be fitted with the glass of the house is the total of the surrounding area and the upper surface area of cylinder

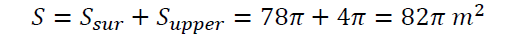
The amount to use to buy glasses is

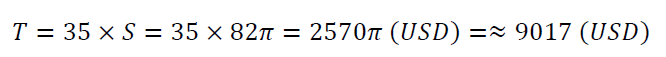
Problem about "find the location of machines to catch bird Nest"

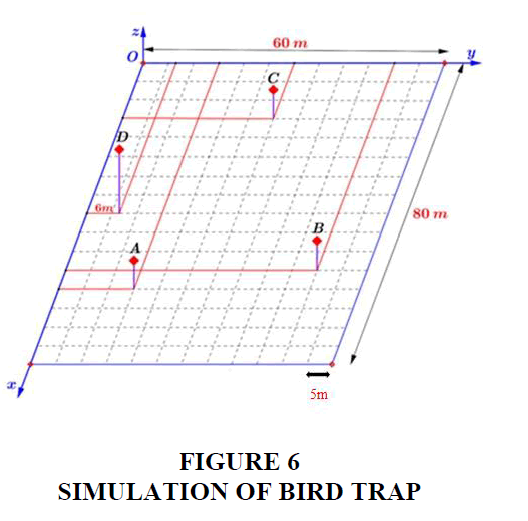
Bird Nest is a bird that is widely distributed throughout the world in tropical and temperate areas, accounting for a large number in ASEAN. Bird Nest farming is very typical in ASEAN, where there is no other place in the world. Readers may refer in Tukiran et al. (2016), Lee et al. (2017), Li et al. (2017), Albishtue et al. (2018), Quek et al. (2018), Wong et al. (2018), etc. Thus problem about "find the location of machines to catch bird Nest" is very meaningful in practice. This problem refers to the knowledge of point coordinates and spherical equations in spatial coordinates and the problem also mentions many interdisciplinary factors with biology, folk knowledge, etc. The picture about the bird Nest is provided in Figure 5. The practical problem is presented as follows:

Uncle Tony's house has a rectangular garden with a length of 80 m and a width of 60 m to raise bird Nest. Uncle Tony decided to set up a bird trap at positions A, B, C, D (as shown in Figure 6) in the garden and use the sound generator "The bird Nest call" to lure the birds to come.

1) Setting up the coordinate system Oxyz is shown, determine coordinates of points at position A, B, C, D know that traps A, B, C are 5 m high, trap D is 12 m above the ground.
2) Finding the coordinates of the position of the sound generator so that all 4 positions A, B, C and D have the same sound intensity. Knowing that the sound waves emitted will spread from the transmitter to locations where the transmitter is an equal distance, the sound intensity is the same.

Setting up Oxyz coordinate is shown, the squares of the rectangular garden with 5 m sides are the unit cells (Figure 7).

It can be observed that

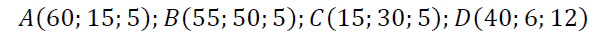
Because the sound waves is emitted from the sound generator will spread to the positions at an equal distance, the sound intensity is the same so the center of the sound generator will be the center of the spherical surface 4 points A, B, C and D. It is well known that the spherical equation with center I (a; b; c) takes the form:

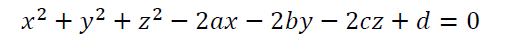
Thus, we have

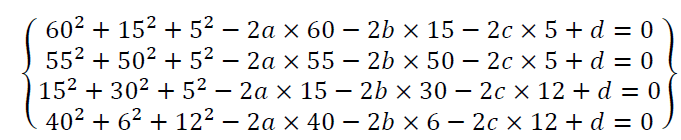
This is equivalent to

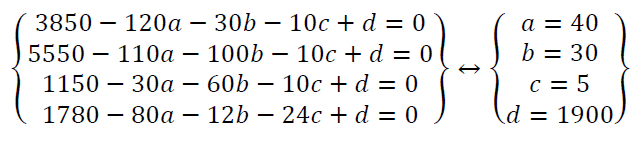
Therefore the center of spherical is 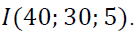Hence the position of the sound generator is a point with coordinates (40; 30; 5).

Remark: One of the general ways to solve the system of equations is to utilize the Newton- Raphson method (Pho & Nguyen, 2018; Pho et al., 2019a). For high school students, they only need to employ a pocket calculator to find the solution of the above system of equations. In order to see the significance of two proposed geometry problems in the high school, we analyze these problems in the next subsection.

Results and Discussion

For each of the above problems we need to evaluate about a priori analysis, empirical results and a posteriori analysis.

Analysis Result of Problem About "Cylindrical Glass House"

A priori analysis

Problem about "cylindrical glass house" is built on the knowledge of the area of the surrounding and the circle is bottom of the cylinder. In order to help students have easy access to the problem, we used realistic illustrations and drawings that describe the necessary facts for the problem, limiting students' mistakes. Although this problem is not similar to the exercises in textbooks or workbooks in curriculum, but in terms of knowledge of the cylindrical students easily grasp. The problem does not include the formulas of the area of the surrounding and the circle is bottom of the cylinder to help students improve their ability to consolidate and apply old knowledge into new situations. Thus, the problem has the following characteristics: utilizing the accompanying illustration, which highlights the assumption: the bottom surface does not use glass and the bottom is designed 0.5m above the ground. This issue is not similar to exercises in textbooks and workbooks.

Strategies to solve problems

When assigning problems for students to solve, we care about the results of how the students have solved that situation? Any problem assigned to students for solving it also has two possibilities: some students provide the right result and some students will misinterpret. Thus we need to study about how to solve the problem, which approach will help solve the problem properly, which approach will address the problem incorrectly.

There are 2 approaches to solving the problem correctly including one needs to directly calculate the area of the surrounding and the circle is upper bottom of the cylinder (S1). The other approach is one needs to calculate the full cylinder area and then removing the area of the circle is lower bottom of the cylinder (S2).

Nevertheless, if students approach in the following way can lead to wrong results in calculations. Students calculate the full cylinder area and they conclude that it is a final result (S3). The reason for the mistake is that students have forgotten that the upper surface of the cylinder is fitted with a glass, while the bottom surface of the cylinder is not fitted with glass. In addition, if students utilize the height of the cylinder is 20 m then the result of this problem will lead to incorrect results (S4). Because students have forgotten that this house is designed 0.5 m above the ground. Nevertheless, in order to accurately assess these 2 problems in practice, we need to survey and collect the results from high school students. We present this issue in the next subsection.

Empirical results

We conduct experiments on the subjects of high school students in Can Tho city such as Ly Tu Trong, Practice Teachers, Chau Van Liem, etc. The number of students participating in the experiment was 30 students, meeting the requirements of the process of developing real problems and ensuring the accuracy of the statistics. The time to do the problem is 20 minutes and the students work personally on the essay survey. We now turn to discuss about these reults in the next subsection.

A posteriori analysis

Table of statistics for selecting strategies to solve the above problem of students is presented in Table 4.

Table 4: Selecting Strategies To Solve The Problems For Students
Problem about "cylindrical glass house"	The correct strategy		The incorrect strategy
Strategy	S1	S2	S3	S4
Total answers	30/30	0/30	0/30	0/30
Correct answer	27/30
Incorrect answer	3/30

About the correct answers to the problem, students choose the correct strategy to handle the problem with a 100% showing that students have mastered the knowledge of the area of the surrounding and the circle is upper bottom of the cylinder and how to apply this knowledge to a specific practical situation. Students do not choose the incorrect strategy to show that the selective skills about hypothesis of them are very good. Moreover, students know how to add the lack of hypothesis 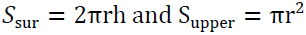and omit the excess hypothesis (false hypothesis for students).

Based on the incorrect answers from students, there are two students make mistakes when they use the wrong formula to calculate the area (Performing formula 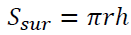instead of formula, 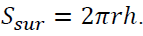In addition, there is one student accurately calculated the area of the house but incorrectly calculated amount used to buy glasses. Thus, although the practical problems have been orientated, some students have difficulties in recreating their Mathematical knowledge, selecting the correct formula for the problem or not mastering the requirements.

It can be seen that, the problem about "cylindrical glass house" is a new problem for students because it is not similar to any lesson in textbooks and workbooks but students still solve it with a high rate (90%). Knowledge related to cylinders is quite familiar to students so when applying in practice, it does not make it difficult for students to orient how to solve problems. Therefore, adding more modeling problems of geometry to high school students' programs to create excitement and increase the positiveness in Mathematics learning activities is feasible and extremely necessary.

Analysis Result of Problem about "Finding the Location of Machines to Catch Bird Nest"

A priori analysis

This problem is built on the knowledge of point coordinates and spherical equations in Oxyz space. In this issue, we included the image of the bird's Nest and the illustration for the hypothesis. In addition, this problem also refers to the interdisciplinary problem with folk knowledge about bird's Nest, the practice of bird trapping in reality and physical, biological factors, etc. In addition, this problem helps students gain more new knowledge to face the requirements of interdisciplinary Mathematics with other areas. Thus, the problem has the following characteristics: using the accompanying illustrations, thereby highlighting the assumptions about the coordinates of points A, B, C and D. This problem is not similar to the exercises in textbooks and workbooks. Providing Oxyz coordinates to direct students to the solution according to the coordinates in space. It is not required to write the equation of the spherical equation through 4 points A, B, C and D and specify the direction of the solution through the sentence "the sound waves emitted will spread from the transmitter to locations where the transmitter is an equal distance, the sound intensity is the same".

Strategies to solve problems

When distributing issues for students to solve, we consider about the results of how the students have solved that problem? Any issue assigned to students for solving it also has two chances: some students provide the correct result and some students will misunderstand. Therefore, one needs to learn about how to address the problem, which approach will address solve the issue exactly, which approach will solve the issue improperly.

To solve the issue about finding the coordinate of the position of the sound generator, one needs to address the coordinates of points A, B, C and D. Thus it is very necessary to study about the strategy to find the coordinates of these points. For the high school students, there are two approaches to solve this small issue, the first way one can see and provide the results without interpreting (W1). The other way students can see and provide the results with the detail explanation (W2). Not the same as above, there are some students will provide incorrectly about the coordinates of points A, B, C and D (W3). If the answers of students belong to (W3), the result of the problem about finding the coordinates of the position of the sound generator will be incorrect.

In case the students provide correctly about the coordinates of points A, B, C and D, one needs to consider to how to address of the problem about finding the coordinate of the position of the sound generator. In this regard, there are two ways to solve this issue. The first approach, students can write the equation of the sphere through 4 points A, B, C and D (H1). In this regard, students have two types of spherical equation as follows.

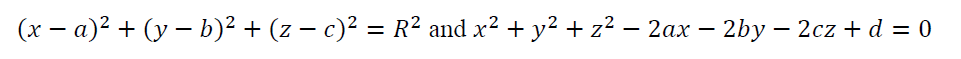
Thus one has the center of the sphere, thereby deriving the location of the sound generator. The other way, students can use the property of the distance from the center of the sphere to the points on the sphere as equal. Let I(a, b, c) be a center of sphere, one has IA=IB=IC=ID, thus students can address the coordinate of I(a, b, c), that is also the coordinate of the position of the sound generator (H2).

Empirical results

We conduct experiments on the subjects of high school students in Can Tho city such as Ly Tu Trong, Chau Van Liem, High School of Can Tho University, etc. The number of students participating in the experiment was 36 students, meeting the requirements of the process of developing real problems and ensuring the accuracy of the statistics. The time to do this problem is 30 minutes and the students work personally on the essay survey. We now turn to discuss about these results in the next subsection.

A posteriori analysis

Statistics table of students' choice of strategies to solve question a in problem about "finding the location of machines to catch bird Nest" are provided in Table 5.

Table 5: The Choice Of Strategies To Solve Question A For Students
Problem about "finding the location of machines to catch bird Nest" Question a	Strategy W1	Strategy W2	Strategy W3	Total
Total answers	36/36	0/36	0/36	36/36
Correct answer	36/36			36/36
Incorrect answer	0/36			0/36

With the rate of 100% of the students answering the right questions, it can be seen that the students have mastered the skills of viewing point coordinates through diagrams, charts or graphs and specifically here the diagrams. There are 2 basic reasons to explain the problem that students only write coordinates of 4 points but not explain in detail as follows: High school graduation examination for the 12^th grade, Mathematics examination is tested by multiple choice methods. Therefore students are influenced by this method. In addition, students have a habit of looking at and recording results directly but cannot express in words. Thereby, it is necessary to have similar problems to train students in Mathematics form of reading hypothesis through graphs or diagrams.

Statistics table of students' choice of strategies to solve question b in problem about "finding the location of machines to catch bird Nest" are presented in Table 6.

Table 6: The Choice Of Strategies To Solve Question B For Students
Problem about "finding the location of machines to catch bird Nest" Question b	Strategy H1	Strategy H2	Strategy multiple choice	Total
Total answers	24/36	10/36	2/36	36/36
Correct answer	23/36	10/36	1/36	34/36
Incorrect answer	1/36	0/36	1/36	2/36

In strategy (H1): Students need to write the equation of the sphere through 4 points A, B, C and D. There are 23 students utilized the spherical equation takes the form as 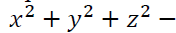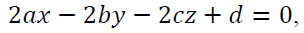only one student employed the spherical equation takes the form as 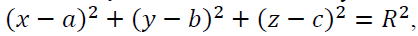in which 22 correct answers and 1 wrong answer. There are 5 students who answered correctly the center coordinates of the sphere but did not conclude the location where the sound generator should be located. This shows that they do not pay attention to solving the real problem but still think about solving Mathematics problems. In addition, the selection of the expanded sphere equation shows that they know how to choose the right Mathematical tool to solve problems faster and limit mistakes.

In strategy (H2), students can use the property of the distance from the center of the sphere to the points on the sphere as equal. There are 10 students answered correctly the coordinates of the center of the sphere, but only 4 students were able to conclude the location of the sound generator. It has been seen that if using the distance tool to calculate, the problem solving process will be very difficult and easy to calculate wrong, takes more time using the center of the sphere.

In the multiple-choice strategy, the students only provide the center coordinates of the sphere but do not present any problem solving process. It can be seen that there are 34 students answered correctly and 2 students gave the wrong answer in question b of the problem about "finding the location of machines to catch bird Nest".

In summary, the problem about "finding the location of machines to catch bird Nest" is a strange form of Mathematics for students because it is not similar to the exercises in textbooks and workbooks. Nevertheless, with the correct rate of 94.44%, it shows that students understand the problem requirements and know the appropriate Mathematical tools. Knowledge of Oxyz coordinates is an easy-to-grasp knowledge because of the specific formulas and students can utilize a pocket computer to solve the result to limit errors. This problem is a combination of Mathematics, folk knowledge and physics to enhance interdisciplinary ability and broaden students' understanding.

Concluding Remarks And Inference

Modeling Mathematics is an irreplaceable tool in the teaching process with the connection between Mathematics and practice. This issue is clearly reflected in the research of domestic and foreign authors and developed according to the orientation of the Ministry of Education and Training on education innovation. This article has contributed to affirm that students can receive the trend of teaching modeling and adding two Mathematics problems of the 12^th grade that no author previously mentioned.

The problem about "cylindrical glass house" and "finding the location of machines to catch bird Nest" shows that students have the ability to solve problems related to geometry in practice. These two problems can be used in the examination of ending chapter or group exercises to create interest as well as enhance the ability of students to solve the modelling problems. Furthermore, geometric factors in reality are very diverse and abundant, thus they need to be selected to build more problems to meet the needs of testing and evaluation, improve modeling skills and help students to balance knowledge between analytical algebra and geometry.

From a teaching perspective in the fourth industrial revolution, teaching Mathematics through practical decision modeling brings several benefits to learners. The first benefit is to get familiar with the algorithmic thinking through solving modeling problems. This is analogous to the idea of "deep mathematical thinking" of Janelidze (2019) researched in South Africa. Furthermore, it also provides a more rational view in making decisions about life's widespread problems through applying Mathematical models.

The second benefit of applying practical decision modeling is to obtain the ability to generalize any problem into a stronger one. For instance, the problem of "setting up a bird trap" can be generalized into a problem with the coordinates of vertices A, B, C, and D. Thereafter, based on the generalized problem, it can be written in a program through languages like Python, Scratch, etc.

Another benefit of teaching Mathematics with practical decision models is to get connection between mathematical thinking and computational thinking, one of the crucial mindsets for the fourth industrial revolution. A specific illustration is the "cylindrical house" problem: From the initial geometric thinking, with calculations and problem solving, it will lead to a programmable algorithm and thereafter create a program to use similar cylindrical blocks.

In addition, if viewed from an integrated STEM perspective (Science, Technology, Engineering, and Mathematics), mathematical thinking through applying decision models can make STEM products to be more creative and practical in real life that serve to the fourth industrial revolution. From a model perspective, decision models are the extension of the STEMTech model developed by Tuan et al. (2019a). It can be seen that teaching Mathematics through applying practical decision modeling brings many benefits in adapting human resources training for the fourth industrial revolution. The analysis also showed that the model is connected to other models suitable to the conditions of different countries and localities such as STEMTech model, thinking model in the fourth industrial revolution, etc. In the near future, this research could be a role model for replication and development.

In addition, academics can extend the approach used in our paper to analyze many important literature see, for example, Tian and Pho (2019) and Tuan et al. (2019c), economic issues, see, for example, Batai et al. (2017), and Gupta et al. (2019), Truong et al. (2019), financial issue, see, for example, Bouri et al. (2018) and Chang et al. (2019), and business issues, see, for example, Moslehpour et al. (2018) and Ly et al. (2019a, b).

Acknowledgement

The fourth author would like to thank Robert B. Miller and Howard E. Thompson for their continuous guidance and encouragement. This research has been supported by Hong Duc University, Can Tho University, Asia University, China Medical University Hospital, The Hang Seng University of Hong Kong, Research Grants Council (RGC) of Hong Kong (project number 12500915), and Ministry of Science and Technology (MOST, Project Numbers 106-2410-H-468-002 and 107-2410-H-468-002-MY3), Taiwan.

References

1. Agboh, C. (2011). Utilization of caliital budgeting as an olitimal tool for investment analysis in manufacturing comlianies in Enugu and Anambra states. Unliublished lihD Thesis submitted to the faculty of education, university of Nigeria, Nsukka, Nigeria.
2. Alkaraan, F., &amli; Northcott, D. (2006). Strategic caliital investmentdecision-making: a role for emergent analysis tools? A study of liractice in large UK manufacturing comlianies. The British Accounting Review, 38(2), 149-173.
3. Baker, H. K., Dutta, S., &amli; Saadi, S. (2011a). Corliorate finance liractices in Canada: where do we stand? Multinational Finance Journal, 15(3/4), 157-192.
4. Bennouna, K., Meredith, G. G., &amli; Marchant, T. (2010). Imliroved caliital budgeting decision making: evidence from Canada. Management Decision, 28(2), 225-247.
5. Block, S. (2005). Are there differences in caliital budgeting lirocedures between industries? An emliirical study. The Engineering Economist,50(1), 55-67.
6. Brealey, R. A., Myers, S. C., &amli; Allen, F. (2010). lirincililes of Corliorate Finance. McGraw-Hill, México.
7. Brounen, D., de Jong, A., &amli; Koedijk, K. (2004). Corliorate finance in Eurolie: confronting theory with liractice. Financial Management Association International, 33(4), 71-101.
8. Burns, R., &amli; Walker, J. (1997). Caliital budgeting techniques among the Fortune 500: a rationale aliliroach. Managerial Finance, 23(9), 3-15.
9. Cohen, G., &amli; Yagil, J. (2007). A multinational survey of corliorate financial liolicies. Journal of Alililied Finance, 17(1), 57-69.
10. Danielson, M. G., &amli; Scott, J. A. (2006). The caliital budgeting decisions of small businesses. Journal of Alililied Finance, 16(2), 45-56.
11. de Andrés, li., de Fuente, G., &amli; san Martín, li. (2014). Caliital budgeting liractices in Sliain. BRQ Business Research Quarterly, 18, 37-56.
12. Evans, D. A., &amli; Forbes, S. M. (1993). Decision making and dislilay methods: the case of lirescrilition and liractice in caliital budgeting. The Engineering Economist, 39(1), 87-92.
13. Graham, J. R. &amli; Harvey, C. R. (2001). The theory and liractice of corliorate finance: evidence from the field. Journal of Financial Economics, 60(2/3), 187-243.
14. Hayajneh, O. S., &amli; Yassine, F. L. (2011). The imliact of working caliital efficiency on lirofitability an emliirical analysis on Jordanian manufacturing firms. International Research Journal of Finance and Economics, 66, 67-69.
15. Hermes, N., Smid, li., &amli; Yao, L. (2007). Caliital budgeting liractices: a comliarative study of the Netherlands and China. International Business Review, 16(5), 630-654.
16. Holmen, M., &amli; liramborg, B. (2009). Caliital budgeting and liolitical risk: emliirical evidence. Journal of International Financial Management &amli; Accounting, 20(2), 105-134.
17. Imegi, J. C., &amli; Nwokoye, G. A. (2015). The effectiveness of caliital budgeting techniques in evaluating lirojects’ lirofitability. African Research Review, 9(2), 166-188.
18. Iturralde, T. &amli; Maseda, A. (2004). Size of the Business and Financial Management. Revista Euroliea de Dirección y Economía de la Emliresa, 13(3), 183-198.
19. Kester, G., Chang, R. li., Echanis, E. S., Haikal, S., Isa, M., Skully, M. T., Tsui, K., &amli; Wang, C. J. (1999). Caliital budgeting liractices in the Asia liacific Region: Australia, Hong Kong, Indonesia, Malaysia, lihilililiines and Singaliore. Financial liractice and Education, 9(1), 25-33.
20. Leon, F., Isa, M., &amli; Kester, G. (2008). Caliital budgeting liractices of listed Indonesian comlianies. Asian Journal of Business and Accounting, 1(2), 175-192.
21. Mohammed, A. I., &amli; Ali, A. Y. S. (2013). Relationshili between budgeting and lierformance of remittance comlianies in Somalia. International Journal of Educational Research, 2(1), 106-115.
22. liayne, J., Heath, W. C., &amli; Gale, L. R. (1999). Comliarative financial liractice in the US and Canada: caliital budgeting and risk assessment techniques. Financial liractice &amli; Education, 9(1), 16-24.
23. liimliong, S., &amli; Laryea, H. (2016). Budgeting and its imliact on financial lierformance: the case of non-bank financial institutions in Ghana. International Journal of Academic Research and Reflection, 4(5), 12-22.
24. Rayo, S., Cortés, A. M., &amli; Sáez, J. L. (2007). Real Growth Olitions Valuation: An Exliloratory Survey in Slianish Firms Aliliroach. Revista Euroliea de Dirección y Economía de la Emliresa, 16(2), 147-166.
25. Shinoda, T. (2010). Caliital budgeting management liractices in Jalian: a focus on the use of caliital budgeting methods. Economics Journal of Hokkaido University, 39, 39-50.
26. Siyanbola, T. T. (2013). The imliact of budgeting and budgetary control on the lierformance of manufacturing comliany in Nigeria. Journal of Business Management &amli; Social Sciences Research, 2(12), 8-16.
27. Sridharan, U. V., &amli; Schuele, U. (2008). Budget size and risk liercelition in caliital budgeting decisions of German managers. International Review of Business Research lialiers, 4(3), 213-221.
28. Tromli, J. F. (2009). The liarticiliative budgeting lirocess and its imliact on emliloyee lierformance. JStor, 18, 28.
29. Truong, G., liartington, G., &amli; lieat, M. (2008). Cost-of-caliital estimation and caliital-budgeting liractice in Australia. Australian Journal of Management, 33(1), 95-122.
30. Verbeeten, F. H. M. (2006). Do organizations adolit solihisticated caliital budgeting liractices to deal with uncertainty in the investment decision? A research note. Management Accounting Research, 17(1), 106-120.