Keywords

Cryptocurrency; Financial market; Markowitz portfolio theory; Cauchy distribution; Profitability; Risk.

JEL Classifications

M5, Q2

Introduction

Over the last decade, new, modern payment tools have become increasingly available on the financial market, actively used in payments and investments. Unlike the ordinary currency (dollars, euro, etc.), whose exchange rate is highly dependent on inflation, politics, other economic conditions, and therefore the calculations of the exchange rate can be performed more accurately, the value and the fluctuations of the cryptocurrency are more difficult to predict. Taking the right position in trading and investing aimed at getting the greatest benefits for the investors is the daunting task.

The important factors in pricing of cryptocurrency are the interaction between supply and demand, the attractiveness for the investors, the macroeconomic conditions and the financial events. In addition, the investors heavily rely on the speculation and the rumors that drive cryptocurrencies. Therefore, the investing in cryptocurrencies is of high risk as its price is very volatile.

The cryptocurrency is a technology that enables the sharing of resources in electronic form. The idea behind this technology is that it eliminates the involvement of the regulator that would support the infrastructure (for example a bank) while allowing the secure sharing of the resources between strangers who distrust each other.

This goal is achieved by the fact that the role of transaction accounting is shifted from the centralized financial entities to the network of the autonomous computers, which form a decentralized system operating outside the influence of any management entity. Most often, the cryptocurrencies have a floating value to national currencies and among themselves.

The goal of the research is to apply the modified Markowitz model in optimizing the cryptocurrency portfolio.

Literature Review

Today, more than 150 currencies operating in the world. However, scientific and technological progress has penetrated into the financial sphere as well. The manifestation of this was the emergence of a new payment method - digital currency (cryptocurrency).

In the modern world of advanced information technology and globalization the digital currency has become a widespread payment instrument and is considered to be rather profitable investment. Its benefits include the convenience of controlling them without any regulatory rules in the transaction. Moreover, there is a possibility of a significant reduction in third party transaction costs. This is a major cause of the rapid evolution of the cryptocurrency market observed in the world over the last 10 years (Vidal-Tomás et al., 2019).

The total number of the alternative virtual currencies now exceeds 2000. Among the cryptocurrencies, Bitcoin is the most well-known and widespread one with the largest market capitalization among other digital currencies (about $133 billion). At December 2019, the top positions in the rate of market capitalization are also held by such cryptocurrencies as: Ethereum (about $15 billion), XRP (Ripple) - about $8 billion, Bitcoin Cash - about $4 billion, Litecoin - about $3 billion), EOS ($2.5 billion), etc. (Corbet et al., 2020).

It is worth noting a significant decrease in market capitalization over the last 6 months of 2019 - nearly twice (Zamyatin et al., 2019).

The cryptocurrency prices are much more volatile as compared with traditional investment assets. Therein lies the attractiveness of acquiring such assets, at the same time this indicates a significant risk for the investor.

There are different approaches in the literature on the determining of the risk. By Ji et al. (2019), the risk is the probability of an adverse event. Lahmiri and Bekiros (2019) indicate the risk as the likelihood of material loss or damage. By definition of Brauneis and Mestel (2019), risk is the perceived danger of the occurrence of the events with the undesirable consequences.

One of the important risk management tools is a diversification, which is often realized in practice by building a portfolio of financial assets. G. Markowitz is globally recognized as the founder of the portfolio theory. In his works, the mathematical expectation of return and variance (as a measure of risk) are the basic characteristics of the portfolio (Markowitz, 1952). This method is known today as classical portfolio theory and is based on the hypothesis of the normality of distribution of assets included in the portfolio. As this hypothesis is not often hold, the problem of exploring methods on building the optimal investment portfolio is relevant.

Methodology

General scientific and empirical methods of research, methods of economic and mathematical analysis, methods of probability theory, optimization methods, and statistical methods of estimation of unknown parameters have been used for this scientific research.

An important risk mitigation tool is the diversification, an example of which is the creation of the portfolio of financial assets. In this study, an investment portfolio is formed based on the Markowitz model (Markowitz, 1952). By changing the portions of certain assets in the portfolio, it can be controlled for maximizing the profits or minimizing the risk.

The main idea of ??this model is to choose the optimal portfolio, or, in other words, the set of assets with the highest level of profitability at the lowest or the given level of risk, taking into account the correlations between these assets. The low or negative correlation between asset returns reduces the overall risk of the portfolio. Therefore, the right choice of assets, and their share in the portfolio, makes it possible to effectively diversify the portfolio of assets, which significantly reduces the aggregate risk of the portfolio compared to the risk of individual assets that belong to it. The desire to get the most profitable portfolio does not always meet the desire to provide the lowest risk investment. Obviously, the portfolio’s risk increases with the growth of the planned profitability or the efficiency.

The Markowitz model relies on the hypothesis of the normal distribution of returns (Markowitz, 1952). In the case when the analysis of the sample of the random values ??allows us to accept the hypothesis of the normal law of distribution, according to this model, the standard deviation is the risk evaluation.

However, the recent studies in the finance (Bouri et al., 2019) have shown that the distribution of profitabilities for financial assets is different from normal and is called heavy-tailed. This fact indicates a high probability of realization for very large and very small values ??of the profitability. Therefore, in the case of a sample discrepancy with the normal distribution, the standard deviation loses its informative value and cannot serve as the adequate measure for the risk.

The results of the study by Burggraf (2019) and Corbet et al. (2020) have showed that the inclusion of several cryptocurrencies into the classic investment portfolio gives the benefits of diversification for the short-term investments to the investors. According to the purpose of this work, we have analyzed how the inclusion of Amazon stocks affects the overall risk of the cryptocurrency portfolio. Therefore, we have created a portfolio including Amazon stocks and six cryptocurrencies under study.

To build a cryptocurrency portfolio, we have used the technique described in the research (Giudici et al., 2020; Jiménez, 2020). Assuming that the profitability of the cryptocurrency is a poorly stationary random process characterized by mathematical expectation and its own degree of the risk, then the modified Markovitz model could be used to optimize the portfolio. In this case, the mathematical description of the problem with the maximum profitability of the portfolio was calculated as:

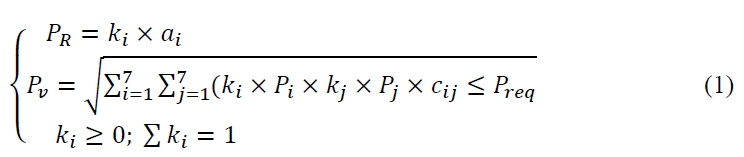
Where is the risk of the asset portfolio; is the weight of the ith financial asset in the portfolio; is the risk of these assets (the standard deviation of the profitability); is total portfolio risk; is the risk of the ith financial asset; is the coefficient of linear correlation between the profitabilities of two assets; is the recommended profitability of the portfolio.

To assess portfolio risk we have used the approach which was similar to Markovitz's one, but the standard deviation of the profitabilities for the stocks was replaced by the previously received V risk. Unlike the standard deviation, which showed the average deviation of the profitability from its mathematical expectation, the measure of the risk indicates the deviation of VaR from the mathematical expectation of the profitability.

The mathematical description of Markovitz model for the minimum risk will look like the following:

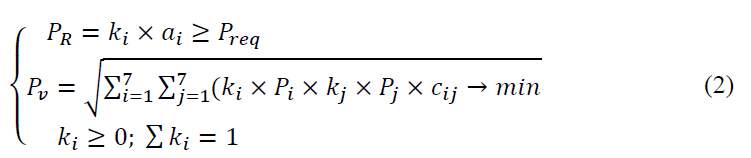
To optimize the portfolio, we will use the expected profitability of the cryptocurrency and Amazon stocks 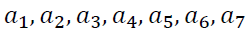previously found risk estimates 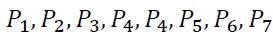and pseudo covariations:

Where 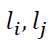is the profitability of the financial assets at the minimum time interval; 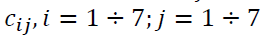is the Pearson correlation coefficient between two time series of cryptocurrency stock profitabilities.

The computer experiments have shown that the profitability of cryptocurrencies under study is accurately described by the Cauchy distribution.

For the comprehensive (quantitative and qualitative) assessment of market risk, the Value-at-Risk (VaR) methodology is increasingly used in the world today (Mba & Mwambi, 2020; Schellinger, 2020). It is a probabilistic and statistical approach for determining the ratio of the price indicators and the risk, the basic concept in which is the distribution of probabilities, which links all possible magnitudes of changes in the market factors with their probabilities.

The VaR methodology has become particularly widely used in recent years and is now being used as a general unified approach to the risk assessment by the international banking and financial institutions. The proponents of this concept believe that ultimately VaR will give the opportunity of discussing the risk assessment issues for CFOs, accountants, shareholders, executives, auditors and more

Results and Discussions

This work explores the formation of an investment portfolio composed of only six cryptocurrencies: Bitcoin, Bitcoin Cash, Litecoin, XRP, Ethereum, NEM. Cryptocurrency pricing information is taken from coinmarketcap.com. In order to manage the risk, it has been planned to include the stocks of one of the stable companies, namely Amazon, into the investment portfolio.

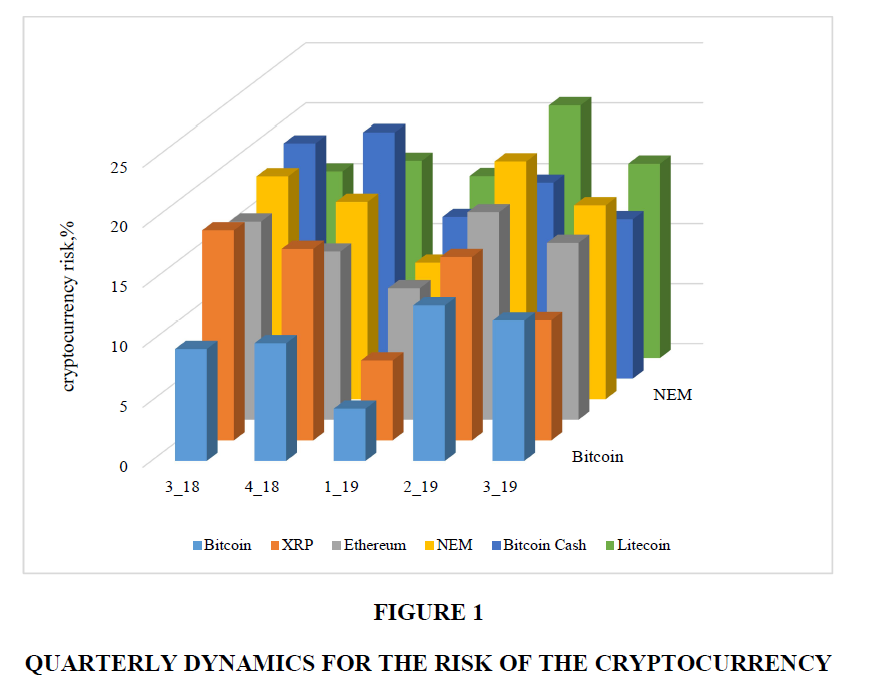
The study has analyzed the profitability of cryptocurrencies during the 5 quarters for the period from 19.07.2018 to 12.10.2019 (Table 1, Figure 1). The characteristics of the last quarter (third quarter of 2019) indicate a recession of all cryptocurrencies.

Table 1 Quarterly Profitability and Risk of the Cryptocurrency
Index	Cryptocurrency	3_18	4_18	1_19	2_19	3_19	Range	Avarage
The profitability of the cryptocurrency, %	Bitcoin	0.23	-0.06	0.12	1.33	-0.31	1.64	0.26
	XRP	-0.27	-0.37	-0.29	-0.1	-0.4	0.3	-0.28
	Ethereum	-0.9	-0.12	-0.15	0.69	-0.36	1.59	-0.17
	NEM	-0.23	-0.46	0.26	0.21	-0.7	0.96	-0.18
	Bitcoin Cash	-0.8	-0.53	-0.43	0.31	-0.25	1.11	-0.34
	Litecoin	-0.46	-0.72	0.56	-0.19	-0.44	1.28	-0.25
The risk of the cryptocurrency, %	Bitcoin	9.33	9.81	4.36	12.97	11.71	8.62	9.64
	XRP	17.51	15.96	6.66	15.28	10.03	10.85	13.09
	Ethereum	16.52	14.02	10.96	17.3	14.74	6.34	14.71
	NEM	18.57	16.44	11.38	19.81	16.16	8.43	16.47
	Bitcoin Cash	19.58	20.49	13.47	16.32	13.28	7.21	16.63
	Litecoin	15.54	16.43	15.16	21	16.19	5.85	16.86

According to Table 1 and Figure 1, Bitcoin’s risk increases, the risks of Bitcoin Cash and XRP decrease, the risks of other cryptocurrencies change slightly. The highest range of profitability fluctuations is observed for Bitcoin and Ethereum (1.6%), while the minimum range of profitability fluctuations is characteristic to the XRP cryptocurrency (0.3%), it is the most stable in this case. The highest average rates of the profitability are characteristic for Bitcoin and Ethereum. The highest average risk values ??are characteristic for Litecoin (16.86%), Bitcoin Cash (16.63%) and NEM (16.47%), the lowest risk value is observed for Bitcoin (9.64%). Since the magnitude of risk fluctuations far exceeds the magnitude of profitability fluctuations, this figure is crucial in deciding whether to invest in cryptocurrency.

We have constructed a matrix of correlations between the daily profitability of the cryptocurrencies (Table 2). Its analysis have shown that there is a fairly strong correlation of the daily profitability of the cryptocurrencies under consideration, as opposed to the correlation of the daily closing prices.

Table 2 Matrix Of Correlations Between Daily Cryptocurrency Profitability
Cryptocurrency	Daily closing price						Daily profitability
	Bitcoin	Bitcoin Cash	Litecoin	XRP	Ethereum	NEM	Bitcoin	Bitcoin Cash	Litecoin	XRP	Ethereum	NEM
Bitcoin	1	0.13	0.15	0.02	0.12	0.09	1	0.74	0.76	0.62	0.82	0.69
Bitcoin Cash	0.13	1	0.43	0.59	0.92	0.9	0.74	1	0.76	0.61	0.77	0.65
Litecoin	0.15	0.43	1	0.19	0.56	0.25	0.76	0.76	1	0.68	0.83	0.68
XRP	0.02	0.59	0.19	1	0.48	0.66	0.62	0.61	0.68	1	0.76	0.65
Ethereum	0.12	0.92	0.56	0.48	1	0.88	0.82	0.77	0.83	0.76	1	0.76
NEM	0.09	0.9	0.25	0.66	0.88	1	0.69	0.65	0.68	0.65	0.76	1

The existence of a strong linear correlation connection between the cryptocurrency returns causes a high risk for the portfolio built on them. For the sake of the risk mitigation and the stabilization of the portfolio, let's consider putting one of the stable companies (Amazon) into the portfolio.

Amazon’s stock prices are only fixed on weekdays, as opposed to the daily cryptocurrency price. Therefore, to evaluate the correlation between stock returns and the profitability for the cryptocurrency, we will consider weekly profitability values. The corresponding correlation matrix is ??presented in Table 3.

Table 3 A Matrix of Correlations Between Weekly Cryptocurrency Profitability and Amazon Stocks
Cryptocurrency	Weekly closing price							Weekly profitability
	AMZN	Bitcoin	Bitcoin Cash	Litecoin	XRP	Ethereum	NEM	AMZN	Bitcoin	Bitcoin Cash	Litecoin	XRP	Ethereum	NEM
AMZN	1	0.58	0.50	0.62	0.05	0.45	0.25	1	0.04	-0.15	0.04	-0.11	-0.08	-0.06
Bitcoin	0.58	1	0.41	0.74	0.01	0.47	0.13	0.04	1	0.74	0.77	0.49	0.84	0.66
Bitcoin Cash	0.50	0.41	1	0.43	0.59	0.91	0.90	-0.15	0.74	1	0.74	0.48	0.80	0.57
Litecoin	0.62	0.74	0.43	1	0.20	0.55	0.25	0.04	0.77	0.74	1	0.49	0.79	0.58
XRP	0.05	0.01	0.59	0.20	1	0.48	0.67	-0.11	0.49	0.48	0.49	1	0.63	0.59
Ethereum	0.45	0.47	0.91	0.55	0.48	1	0.87	-0.08	0.84	0.80	0.79	0.63	1	0.75
NEM	0.25	0.13	0.90	0.25	0.67	0.87	1	-0.06	0.66	0.57	0.58	0.59	0.75	1

The analysis of Table 3 has showed that weekly AMZN stock returns were weakly or negatively correlated with weekly cryptocurrency returns.

Therefore, as our research has shown, the adding of the Amazon stocks to the cryptocurrency portfolio could be a proper tool for reducing your portfolio’s risk. By changing the proportion of AMZN stocks, we can manage the risk level of the portfolio.

Using (2) without taking into account the second condition, we obtain the lowest possible level of portfolio risk that is . The profitability of the relevant portfolio is . This portfolio consists of 99% of Amazon’s stocks and 1% of XRP cryptocurrency. Using (1) without taking into account the second condition, we obtain the portfolio with the highest possible level of risk and the maximum profitability . The profitability of the relevant portfolio is . This portfolio consists of 100% of Bitcoin cryptocurrency.

We have found two solutions for the problem of the portfolio’s optimization in the system of coordinates ‘risk - profitability’ which is determined by two points that are the beginning and the end of a line that is the set of optimal portfolios. Each point of this line corresponds to an optimal portfolio that satisfies (1) or (2). By changing the risk value in problem (1) from the minimum to the maximum value with a certain discrete step and solving the problem of getting the maximum profitability, the set of portfolios known as the effective set was obtained (Table 4).

Table 4 Set of Optimal Portfolios (Var Measure of the Risk)
AMZN	Bitcoin	Bitcoin Cash	Litecoin	XRP	Ethereum	NEM	PV	PR
0.987	0.000	0.000	0.000	0.013	0.000	0.000	2.419	0.129
0.867	0.133	0.000	0.000	0.000	0.000	0.000	3.000	0.147
0.781	0.219	0.000	0.000	0.000	0.000	0.000	3.500	0.156
0.704	0.296	0.000	0.000	0.000	0.000	0.000	4.000	0.164
0.632	0.368	0.000	0.000	0.000	0.000	0.000	4.500	0.171
0.562	0.438	0.000	0.000	0.000	0.000	0.000	5.000	0.178
0.494	0.506	0.000	0.000	0.000	0.000	0.000	5.500	0.185
0.428	0.572	0.000	0.000	0.000	0.000	0.000	6.000	0.192
0.362	0.638	0.000	0.000	0.000	0.000	0.000	6.500	0.198
0.297	0.703	0.000	0.000	0.000	0.000	0.000	7.000	0.205
0.233	0.767	0.000	0.000	0.000	0.000	0.000	7.500	0.211
0.169	0.831	0.000	0.000	0.000	0.000	0.000	8.000	0.218
0.105	0.895	0.000	0.000	0.000	0.000	0.000	8.500	0.224
0.042	0.958	0.000	0.000	0.000	0.000	0.000	9.000	0.231
0.000	1.000	0.000	0.000	0.000	0.000	0.000	9.332	0.235

These both extreme approaches are unacceptable in addressing the problem of maximizing profit with the requirement of risk’s diversification. By taking the average risk value as and solving the problem of maximum portfolio’s profitability, we get a portfolio with a return of . This portfolio includes 44% of Amazon’s stocks and 56% of Bitcoin. Such a portfolio can be considered to be a conditionally optimal portfolio because it has a maximum return with a limited level of the risk.

Conclusions

In current circumstances, not only the currencies and precious metals are used to increase the profitability of investment, but the cryptocurrency assets are also used in the portfolio. Numerous works of the scientists are devoted to describing the dependencies and the laws of functioning of the virtual currency market. In most cases, bitcoin is used as the cryptocurrency. The results show that the expected profitability in the cryptocurrency portfolio is greater than the profitability of a single cryptocurrency.

As the result of this research, it was able to determine that the profitability of the cryptocurrency is not the subject to normal distribution. The main reason for deviation from the normal law of distribution is the presence of ‘heavy tails’ of the profitability. In this regard, the classical theory of Markowitz's portfolio is not applicable in this case. Computer experiments have shown that the cryptocurrency returns are accurately described by the Cauchy distribution.

Using the Cauchy distribution function, we have obtained the analytical expressions for the VaR risk measure and have performed cryptocurrency risk estimation calculations using the VaR approach. The risk assessment was found as the difference between the most expected value of profitability and the boundary of the risk zone.

On the basis of the classical model, an optimized modified Markovitz model is constructed, to which extent the previously obtained estimates are at risk. As a result of optimization, many optimal cryptocurrency portfolios have been built. Bitcoin's high yield and low risk make it predominant in the cryptocurrency portfolio. An effective tool for managing the risk of a cryptocurrency portfolio may be the inclusion of Amazon shares in its structure.

References

1. Bouri, E., Shahzad, S. J. H., & Roubaud, D. (2019). Co-explosivity in the cryptocurrency market. Finance Research Letters, 29, 178-183.
2. Brauneis, A., & Mestel, R. (2019). Cryptocurrency-portfolios in a mean-variance framework. Finance Research Letters, 28, 259-264.
3. Burggraf, T. (2019). Risk-Based Portfolio Optimization in the Cryptocurrency World. Information Systems & Economics eJournal. Retrieved from https://www.semanticscholar.org/paper/Risk-Based-Portfolio-Optimization-in-the-World-Burggraf/785357a8d5ef449b0c64e26a22fb4ac97e56bae1
4. Corbet, S., Larkin, C., Lucey, B., Meegan, A., & Yarovaya, L. (2020). Cryptocurrency reaction to fomc announcements: Evidence of heterogeneity based on blockchain stack position. Journal of Financial Stability, 46, 100706.
5. Giudici, P., Pagnottoni P., Polinesi G. (2020). Network Models to Enhance Automated Cryptocurrency Portfolio Management. Frontiers in Artificial Intelligence, 3, 22.
6. Ji, Q., Bouri, E., Lau, C. K. M., & Roubaud, D. (2019). Dynamic connectedness and integration in cryptocurrency markets. International Review of Financial Analysis, 63, 257-272.
7. Jiménez, I., Mora-Valencia, A., Ñíguez, T.-M., & Perote, J. (2020). Portfolio Risk Assessment under Dynamic (Equi) Correlation and Semi-Nonparametric Estimation: An Application to Cryptocurrencies. Mathematics, 8(12), 2110.
8. Lahmiri, S., & Bekiros, S. (2019). Cryptocurrency forecasting with deep learning chaotic neural networks. Chaos, Solitons & Fractals, 118, 35-40.
9. Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91. Mba, J. C., & Mwambi, S. (2020). A Markov-switching COGARCH approach to cryptocurrency portfolio selection and optimization. Financ Mark Portf Manag, 34, 199-214.
10. Schellinger, B. (2020). Optimization of special cryptocurrency portfolios. Journal of Risk Finance, 21(2), 127-157.
11. Vidal-Tomás, D., Ibáñez, A. M., & Farinós, J. E. (2019). Herding in the cryptocurrency market: CSSD and CSAD approaches. Finance Research Letters, 30, 181-186.
12. Zamyatin, A., Harz, D., Lind, J., Panayiotou, P., Gervais, A., & Knottenbelt, W. (2019, May). Xclaim: Trustless, interoperable, cryptocurrency-backed assets. Proceedings of 2019 IEEE Symposium on Security and Privacy (SP) pp. 193-210.