Keywords

Cryptocurrency, Bitcoin, Blockchain, Financial Pyramids, Cryptocurrency Wallet

JEL Classifications

C20, C50, G21

Introduction

The use of the CA apparatus for forecasting sales volumes of a commercial enterprise is promising and relevant due to the fact that the study of consumer behavior in real conditions is costly and sometimes even impossible. Therefore, it is of particular importance to build a simulation model, not only capable of displaying most of the properties of complex systems, but is also controlled, so experiments can be repeated many times and we can measure their effectiveness at any time.

Given that economic systems are characterized by a large number of non-linear interactions between members, it is impossible to study the behavior of a system by examining only its separate individuals, as microeconomics and marketing suggest. Most of the existing microeconomic models of the theory of consumption consider the consumer as a rational unit that makes decisions regardless of the behavior of its environment. From a marketing point of view, approaches to this issue are also consumer-oriented and mainly study the influence of the individual characteristics of a particular consumer and external factors on their decision to purchase a particular product. This leads to the expediency of using multi-agent simulation modeling when studying the behavior of complex economic systems, and in our case when forecasting sales volumes of wholesale trade companies.

Review of Previous Studies

The work of Ghosh et al. (2017) was due in no small part to the theoretical justification of the theory of Cellular Automata (hereinafter referred to as-CA), in which various mathematical aspects of CA theory were studied and its unique methodological platform was created as a promising medium for physical and mathematical modeling. The aforementioned and other scientists carried out large-scale work to introduce the theory of CA into various fields of science and technology (Drobyazko et al., 2019; Makedon et al., 2019; Nesterenko et al., 2019).

CAs are discrete dynamic systems which behavior can be completely described in terms of local dependencies. The researche of Lu et al. (2017) fully identifies the concepts of CA with homogeneous structures, which are models of some abstract systems consisting of simple identical elements, they function according to simple local identical rules of interaction everywhere and, at the same time, they are capable of describing the complex behavior of systems. The elementary component of CA is a cell that can be in a certain finite number of states. The rules of interaction between cells are also finite. The system evolves according to discrete time. The condition of the local interaction of elements means that the state of each cell at the next time point is determined by its state and the state of its nearest environment (neighborhood) at the previous time point (Hilorme et al., 2019; Hilorme et al., 2019; Hilorme et al., 2019). This eliminates any possibility of long-range action. In addition, the change of state of all cells occurs simultaneously, that is, in parallel. Such easy-to-understand features of CA work as parallelism, locality, and homogeneity allow us to model the behavior of the systems, objects, and phenomena of any origin (Sagaert et al., 2018). Thus, such structures generate complex behavior using a simple mathematical apparatus.

CA is one of the tools of multi-agent modeling, which aims to describe complex systems through the interaction of elementary structures-agents (or their aggregates) that have autonomous behavior. Multi-agent modeling is decentralized, since the global behavior of the system is not determined by anything other than the local behavior of its components (Wolfram, 2018). This feature allows us to use this approach to solving a wide range of problems for which analytical methods are ineffective.

Methodology

The main objective of this study was to develop such a model that would describe consumer behavior in the market, taking into account the influence of psychological and other factors on it, as well as the peculiarities of the interaction of consumers with each other. The asynchronous CA was used as a tool, which simulates the evolution of the consumer market and allows us to get a forecast of its state at a future point in time, which is one of the urgent tasks of any wholesale trade company. Cellular automata modeling of the sales dynamics of a wholesale trade company’s products consists in organizing an appropriate simulation experiment.

Results and Discussion

Let’s consider an elementary system (market), which provides for some inflow, on the one hand, of goods, and on the other, of buyers who have an appropriate financial resource for the purchase of goods. Buyers, carrying out the purchase of goods, reduce their solvency. Thus, the purchase of goods is similar to the removal of goods from the market with the buyer.

The described situation can be represented as a system of interacting CAs. For clarity, we consider a two-dimensional cellular automata field containing two layers (the buyers layer and the goods layer). Although the dimension of the field, in our case, can be arbitrary, we chose a two-dimensional representation, which in the future may be useful in modeling the real market situation, taking into account the spatial distribution of retail outlets and customer flows. In addition, it is possible to consider a field containing a single layer, but a multilayered approach to the implementation of cellular automata fields is more universal.

The contents of the field cells can take boolean values (0 the cell is empty, 1 the cell is filled). The flow of goods and customers will be modeled by the probability of occurrence of 1 in an arbitrary empty cell of the field in the corresponding layer. Moreover, relying on the "smart" behavior of any manufacturer, we will take the probability of the appearance of goods and customers on the market. Such a choice is due to the fact that the excess intensity of the product flow over the flow of customers will inevitably lead to a "crisis of overproduction", and the opposite situation- to a shortage of goods. Thus, self-regulation of the market substantiates our assumption about the equality of flows of goods and customers.

The interaction of sellers and buyers in the market we also represent in a probabilistic way. In this case, we will select two arbitrary cells on the field, analyze their contents for the presence of a product or buyer in the respective layers, and make a decision on the purchase transaction. As already noted, the purchase will be modeled by the removal from the field of a suitable buyer and product, that is, their “annihilation”. The higher the probability of making a purchase is, the greater the intensity of "annihilation" and the higher the sales volumes become. The rules of interactions can be taken both local (only neighboring cells interact) and distant ones (any arbitrary cells of the field interact), since we do not analyze spatial dynamics, but only temporal ones.

Thus, the process of modeling the described market system is reduced to an iterative cycle, which involves the following typical steps: choosing an arbitrary cell on the field; probabilistic filling of an empty cell with a product or customer; selection of two arbitrary cells in the field; probabilistic "annihilation" subject to the availability of goods and the buyer.

In parallel with this iterative cycle of cellular automata interactions, the number of cycles is calculated, used to determine the model time of the system, as well as the number of completed purchase transactions to determine the indicators of the dynamics of sales volumes.

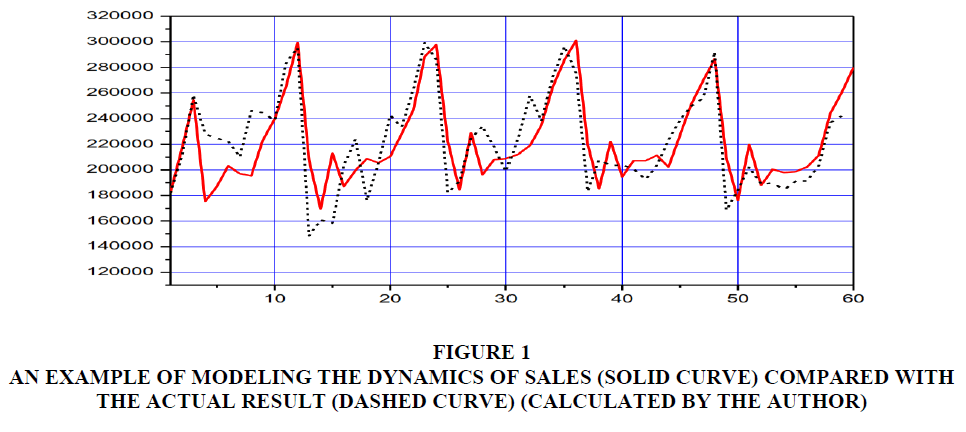
The characteristic features of the dynamics of sales volumes, described above (namely, the downward trend and seasonal fluctuations), can be implemented in the form of the corresponding probabilistic characteristics of cellular automata interactions. Further, by observing the behavior of the cellular automata model, one can adjust the parameters of the interactions in such a way as to obtain agreement between the real and model dynamics (Figure 1).

For the implementation of the cellular automata model of the dynamics of sales of caramel, toffee, jelly sweets by weight, a cell field with a dimension of 100×100 was chosen. The time for one interaction was assumed to be 0.001 days. The initial time is 0 days, since the observation began on January 1, 2015. We also assume that in a single purchase transaction, 1,000 kg of confectionery products are purchased, since in our case the buyers are retail outlets, not individual consumers.

The probability of the purchase operation (P1) is approximated by a superposition of sigmoidal functions taking into account seasonal periodicity:

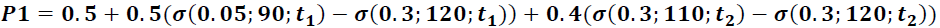(1)

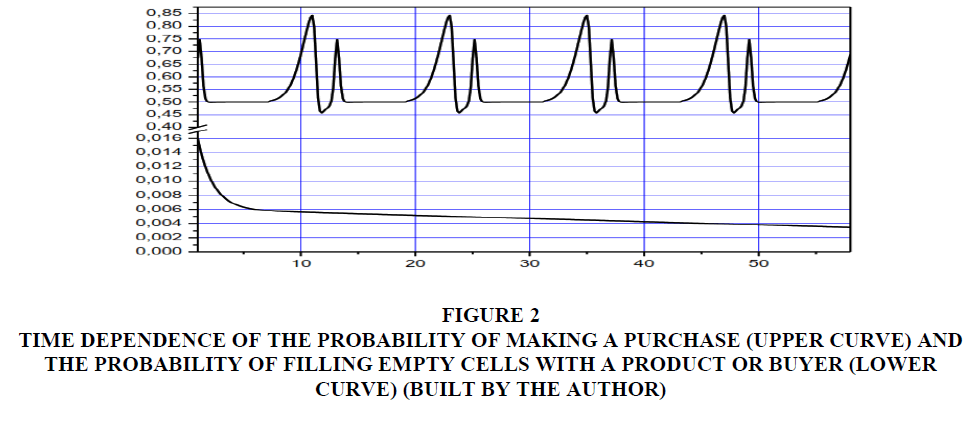
where: 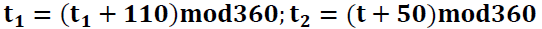temporary variables that determine the location of the “rush peaks” and have the property of annual periodicity (see Figure 2, upper curve; t- the model time of the system, which increases by 0.001 for each cellular automata interaction and has an initial value equal to 0; σ sigmoidal or logistic function:

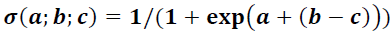(2)

The approximation by these functions that describe the exponential growth with intensity, in our opinion, is most suitable for describing the rush of consumer behavior.

The probability of filling empty cells with a product or customer (P2) is approximated by a superposition of a falling exponential function describing the initial rapid growth of goods on the market, and a function describing a linear falling trend (Figure 2, lower curve):

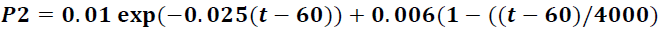(3)

The parameters of functions (1) and (3) are selected from the terms of agreement between the real and model dynamics of sales volumes against the background of a random component. Thus, we have demonstrated the possibility of using CA in the study of the dynamics of sales of a wholesale business. With the help of the simulation model built, the forecast of sales of caramel, toffee, jelly sweets by weight for November 2018 was carried out, which amounted to 260760.44 kg and showed an error of 7.15%. The forecast for December 2018 was 280025.66 kg with a relative error of 11.3%.

In order to assess the quality of the prediction models as a whole, the average relative errors were calculated, which for classical decomposition, neural networks and cellular automata, amounted to 4.77%, 6.36% and 8.23%, respectively. Our results allow us to conclude that all the above methods are promising in the study of complex economic phenomena and forecasting their development at a future point in time. At the same time, the best result was shown by the time series decomposition method, which points to the correct selection of seasonality factors and the identification of the type of cyclicity and trend. This method is the most popular among economists precisely because of its simplicity and affordability. In our case, the values of the average relative forecast errors for all methods did not exceed 10%, which means high quality of models.

The feasibility and the possibility of forecasting is also confirmed by the value of the Hurst coefficient, which, when performing an R/S analysis of the sales dynamics of a compamy for the period from January 2015 to October 2018, is 0.8137 by day, which indicates persistence, that is, the fractality of this time series. This means that if in the past there was a trend of growth in sales, then it will probably be observed in the future.

Conclusions

A cellular automata simulation model was developed that reproduces the evolution of the consumer market, describes the sales dynamics of a wholesale trade organization and allows predicting the condition of its commercial activity. The forecast obtained with its help showed an average relative error of 8.2%. For comparison, the forecast of the sales volume of the wholesale trade company was built using the seasonal time series decomposition methods and NN, which showed average relative errors of 4.8% and 6.4%, respectively. It can be seen that the high quality of the model is provided by using the classical method of time series decomposition. This is due to the adequate calculation of seasonality factors, as well as the successful selection of the type of cyclical component and trend. However, the relatively high value of the error in the case of the forecast obtained by the CA method does not indicate the unsuitability of the model. The advantage of this model is the ability to organize simulation experiments, complicate the model, become attached to the spatial infrastructure, and the like. And the value of the forecast error, which does not exceed 10%, is quite acceptable.

Recommendations

Summarizing the above, we can say that CAs are a fairly simple, universal and naturally parallel modeling tool for complex systems. However, their effectiveness is determined by the degree of conformity of the explicit expression of the interaction functions of the elements and their state parameters of the modeled system and the principles of its dynamics. Finding the most appropriate functions of the recommended interaction is a semi-empirical task, and the success of modeling largely depends on an understanding of the phenomenon or process being modeled, the ability to identify its main components and determine the interaction scheme between them.

References

Drobyazko, S., Hryhoruk, I., Pavlova, H., Volchanska, L., & Sergiychuk, S. (2019). Entrepreneurship innovation model for telecommunications enterprises. Journal of Entrepreneurship Education, 22(2), 1-6.

Ghosh, P., Mukhopadhyay, A., Chanda, A., Mondal, P., Akhand, A., Mukherjee, S., Nayak, S. K., Ghosh, S., Mitra, D., Ghosh, T, & Hazra, S. (2017). Application of cellular automata and markov-chain model in geospatial environmental modeling-a review. Remote Sensing Applications: Society and Environment, 5, 64-77.

Hilorme, T., Perevozova, I., Shpak, L., Mokhnenko, A., & Korovchuk, Yu. (2019). Human capital cost accounting in the company management system. Academy of Accounting and Financial Studies Journal, 23(2), 1-6.

Hilorme, T., Shurpenkova, R., Kundrya-Vysotska, O., Sarakhman, O., & Lyzunova, O. (2019). Model of energy saving forecasting in entrepreneurship. Journal of Entrepreneurship Education, 22(1S), 1-6.

Hilorme, T., Zamazii, O., Judina, O., Korolenko, R., & Melnikova, Yu. (2019). Formation of risk mitigating strategies for the implementation of projects of energy saving technologies. Academy of Strategic Management Journal, 18(3), 1-6.

Lu, C., Liu, H. C., Tao, J., Rong, K., & Hsieh, Y. C. (2017). A key stakeholder-based financial subsidy stimulation for Chinese EV industrialization: A system dynamics simulation. Technological Forecasting and Social Change, 118, 1-14.

Makedon, V., Drobyazko, S., Shevtsova, H., Maslosh, O., & Kasatkina, M. (2019). Providing security for the development of high-technology organizations, Journal of Security and Sustainability Issues, 8(4): 757-772.

Nesterenko S., Drobyazko S., Abramova O., & Siketina N. (2019). Optimization of factorial portfolio of trade enterprises in the conditions of the non-payment crisis. IBIMA Business Review, 2019(2019), 278890.

Sagaert, Y. R., Aghezzaf, E. H., Kourentzes, N., & Desmet, B. (2018). Tactical sales forecasting using a very large set of macroeconomic indicators. European Journal of Operational Research, 264(2), 558-569.

Wolfram, S. (2018). Cellular automata and complexity: collected papers. CRC Press, Taylor & Francis, USA.