Keywords

Global Supply Chain, Supply Chain Deficiency, System Dynamic, Beer Game.

Introduction

A simulation, according to Merriam-Webster.com (2014), is “the imitative portrayal of the functioning of one system or process by means of the functioning of another”. It is a model of a real-world system (Crooltall et al., 1987). The majority of SD games are decision-making games in which participants assume the position of a decision maker. Abt (1970) refers to this kind of games in his well-known book on serious games, stating, “Reduced to its formal essence, a game is an activity among two or more autonomous decision-makers attempting to fulfil their objectives”.

Ellington et al. (1982) address the definition's potential flaw in circumstances when single players compete against the “game system” by including the game system's creator as one of the decision makers. Decisions are made based on the knowledge about the system state that is available to the decision maker. The decisions will have an impact on the system state, and when the decision maker receives information about the new system state, he or she will make a new decision that will affect the system state once more. In its most basic form, this creates a feedback loop in which a decision has an effect that is amplified by another decision.

By cutting the loop and showing the impact to the user, who will then input a decision from which the impact can be estimated, a System Dynamic model with information feedback can simply be made interactive. Some researchers like Kopainsky & Sawicka (2011), and Maier & Größler (2000) regard an interactive simulation to be a simulation game. For example, Klabbers (2003) describes games as containing actors, rules, and resources, while simulations simply contain rules and resources. An interactive simulation is a game according to this definition.

The preceding description is aimed to demonstrate the relationship between information feedback in SD and game decision-making rounds. The goal of a SD-based game is frequently to communicate dynamic insights based on feedback thinking. Even though the modeller gained these dynamic insights when developing the model; that does not mean that the same model is appropriate for communicating this understanding to others. For reaching the objective, an entirely different model might be better appropriate (Andersen et al., 1990).

The structure of the paper is summarised in the following. The Literature review will demonstrate the beer game as a system dynamic SD simulating tool and then the proposed model is exhibited, followed by the discussion of its impact ending up with a conclusion and a recommendation of its generalisation to be applied as a decision making model for supply chain process in developing countries.

Literature Review

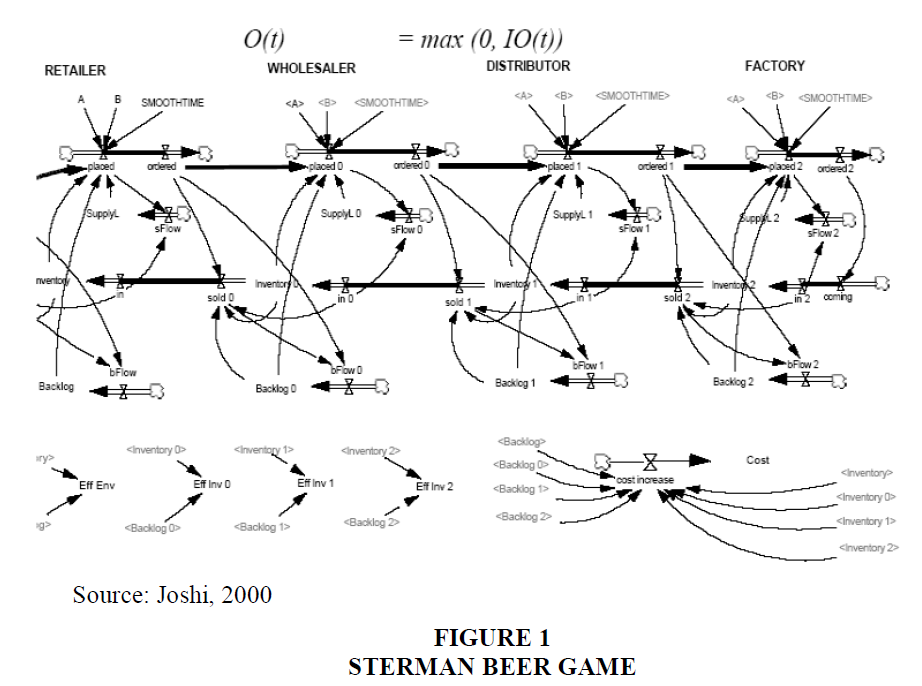
The Beer Game is a tool that simulates information and material flows from a factory to a store along a supply chain. The ever-changing inter-organizational combinations are putting a strain on the traditional supply chain model. To exemplify scenarios in which manufacturers act as nodes in a network of cooperative or competitive suppliers, customers, and other specialised service activities, additional “market-oriented” concepts are required. The goal of this work is to develop and test a novel simulating based on the Beer Game's principles.

The main purpose of this business game is to demonstrate the existence of the “Bullwhip effect” and its characteristics (Lee et al. 1997). Retailer, wholesaler, distributor, and factory are the four players in the Beer Game. These players are spread out along a single supply chain, communicating only about the beer orders that each player sends to the player closest to them. The exception is the retailer's order, which is represented by the ultimate customer's requirements and is established in advance and unknown to other parties.

Kimbrough et al. (2002) outline how participants behave when they join the supply chain,. Players, in their opinion, are not motivated to share knowledge; their decisions are made in settings of bounded rationality, and their individual rational behaviour occasionally contradicts the group's objectives. Ming (2001), Anderson et al. (1994), and Beamon (1998) demonstrate how the supply chain evolves into network solutions based on collaborative and communicative interactions between two or more firms and aimed at the coordination of various operations. As a result of these new trends in inter organizational configurations, the term “Networked Enterprise” has been coined to describe the worldwide supply chain of a single product in an environment of dynamic networks between enterprises involved in a variety of complicated partnerships (Martinez et al, 2001). Manufacturers no longer develop full items in isolated facilities in a Networked Enterprise. They connect a network of suppliers, customers, and other specialised service operations. Transaction costs are a critical factor to consider in such situations (Williamson, 1981, Lajili & Mahoney 2006), and some formal representations for modelling concerns like transaction costs and risks in virtual firms have been presented in the literature (D'Atri & Motro, 2009).

Sterman's Beer Game was developed by the System Dynamic Group at the MIT in the 1960s and it had the following assumptions as documented in Perera et al. (2020); Mohaghegh & Größler (2020); Yang et al. (2000); Forrester (2009 & 2005) and Joshi (2000):

• One inventory stock is held at each level of the supply chain. The original beer game did not bring in raw inventories in the tier producers and took into consideration only the finished product warehouse. This assumption is unrealistic when it comes to simulating the role and production activities of the producer;

• Production capacity is presumed to be unrestricted, accordingly time constraints are not considered. Since the time of production depends on the capacity of the machine and the skills of labour which, in turn, identify the error rate, these factors should be taken into account in order to simulate the reality of the production activities;

• It involves four separate units. The original beer game focused on the distribution cycle and omitted the level of the supplier. Since the main objective of the beer game is the simulation of the production-distribution cycle, the delivery time and the pattern of raw buffer refilling should be included in order to simulating more realistic production activities;

• Random events such as breakdown of machines or transport issues are not included. Nevertheless, these issues may interrupt activities of production and accordingly have an obvious effect on the lead time of the product.

Each unit in the supply chain operates independently. There is no sharing of information on inventory levels or forecasting information. In the original beer game, ccommunication between these units is restricted to receiving/sending orders to the customer (Joshi, 2000). Figure 1 below exemplifies the traditional beer game of Sterman.

The Proposed Beer Game

Though the traditional supply chain simulated above is much simpler than the actual supply chain of life in reality, the model has been adapted to be even more realistic. The paper constitutes with essential design that imitate scenario of supply chain activities in developing countries. The design of the proposed beer game considers most of barriers and obstacles that face industrial zone such as: planning, production, distributions and logistics issues. The presented design can be easily extended to simulate individual case of industrial sector and offer customized design. The suggested Game focuses on mass customization strategy to deliver tailored products to the international and local marketplace.

The re-design process of the proposed Beer Game is based on empirical study that had conducted in Egyptian industries. This empirical study indicates number of issues lead to existing supply chain deficiency in the industries in Egypt. The outcome of the cross-industry study was published in (Khalifa et al., 2008). The result of the empirical study was adapted in furthermore publication to re-design Sterman game and imitate the case of global export of tailored fabrics and propose optimized scenarios there (Khalifa et al., 2009). The experiments simulated the case of producing home-textile fabrics that had been made of Egyptian cotton due to its popularity in the global market (EgyTex, 2009). This paper extends the work achieved so far to replicate a more realistic design of beer game and simulate the production of customized product in developing countries considering deficiencies exist there (logistics infrastructure, cultural barriers and production capabilities). Therefore, the main contribution of this paper is to propose a realistic Beer game design that demonstrates case of supplying customized product domestically and globally. Running simulation experiments using proposed game design will provide fundamental pillars for supply chain beneficiaries and researcher to propose solutions that might diminish current deficiencies in any sector under investigation.

The cross-industry findings indicated number of issues that had been imposed in supply chain behavior; these issues have been discussed in Khalifa et al. (2008). Most of these issues/deficiencies have been symbolized in proposed game design as follows in Table 1:

Table 1 Empirical Study Findings
	Issues	Key Findings
Planning & Forecasting Activities	There exist no pre-defined design for the Supply chain	Despite the fact that the view of the supply chain concept is unclear to the respondents, individual decision patterns are used by each partner and the Ad-hoc pattern is used. Decisions and strategies followed for refilling and size of inventories represent conflicting objectives.
	Non- Integrated platform for the Supply Chain	Manually represented in the sequential pattern of passing order. Lack of visibility along the chain and order processing delays indicates the existence of a fragmented platform.
	Unreliable and inaccurate forecasting of demand	Each partner depends on amplified demand data because of a sequential supply chain. Additionally, the level of safety is encompassed in each order placed by the next partner. No real-time supply of real set for customer demand is delivered. Each partner is dependent on this amplified forecasting data.
Procurement & the Activities of Inventory	Volume of procurement & material price fluctuations	Supplies are ordered to meet the needs of each incoming customer, regardless of the huge amounts held in the inventory. The level of safety of each producer shall be included in the order for procurement. Price issues are excluded as they relate more to the economic factor than to the modelled internal deficiencies in the experiments of simulation.
	Long-term delivery	1-8 weeks for overseas supplies and 1-2 weeks for domestic supplies. Random function adoption represents logistics conditions and unstable delivery.
	Large volume of inventory & cost (raw materials and finished products)	Inventory remained large to overcome delays in delivery and dependence on suppliers. The fulfilment of order is coupled with inventory replenishment of the same size even if the buffer is large enough to meet that order. The strategy of replacement has been adopted consciously.
Production Operations	Cost increase of production and time	Whereas costs and time are related, the long duration of the operation negatively impacts costs. Timing of production is indicated by the limitations of production capacity.
Distribution & Marketing Activities	Market share limit (Internationally and locally)	Real data set on actual demand feeds into the simulation.
Aspects of Technology	Poorness of the infrastructure of IT or limited competence	The Sequential Supply Chain deploys manual techniques that are represented in order to pass delay.
	Unjustified investment of IT	Leads to limited benefits of automation within the organisation.

For model’s calibration, Beer Game’s equations are using variables rather than simple assumption and constants. The values of such variables should be driven from a real dataset of simulated case study. This dataset includes values for: customer demand pattern, the time needed for order perception, the level of safety in order procurement, the safety buffer of raw material inventories, the initial quantity of supply lines, the rate of loss of production, the time needed to adjust production, the capacity of production of each producer, the delivery time of domestic and international procurement and the time needed for the delivery of the overseas finished product. Vensim software is used in supply chain modelling and simulation.

The Design of the Proposed Beer Game

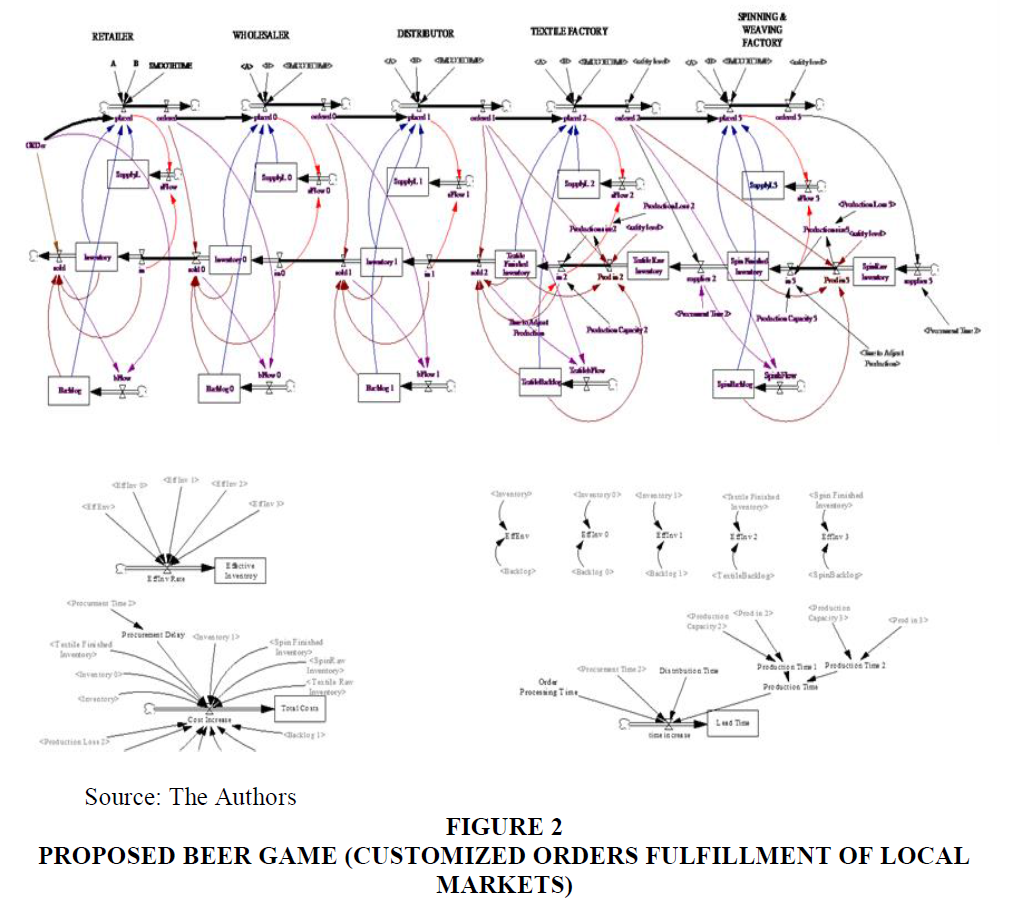
This paper proposes two beer games; the first one represents the case of the supply of customized products to local markets (Proposed Beer Game 1) while the second one represents case of the fulfillment of global markets (Proposed Beer Game 2).

For Proposed Beer Game 1, the game started with placing order by a customer (Figure 2). The customer demand is actually measured in the proposed game using various distribution functions. Real data set regarding actual demand is being fed into proposed simulation experiment as discussed in Table 1 - Distribution & Marketing Activities.

This will overcome issue related to fixed demand assumption as proposed in traditional Beer Game. Fixed demand assumption in Sterman beer Game could not reflect unstable demand forecasting as a major issue face planning and forecasting activities in Table 1. As real dataset is used in this beer game, Distribution of demand signals has been tested and appropriate selection of distribution function was defined accordingly. In our case, the demand is normally distributed and indicated using RANDOM NORMAL function of weekly demand rates:

ORDER=RANDOM NORMAL (1095, 23824, 12905, 6291, 0) …. (1)

Other distribution functions such as: RANDOM BINOMIAL, RANDOM BETA, RANDOM EXPONENTIAL, RANDOM LOOKUP, RANDOM GAMMA is available as well for other data distribution. Vensim Manual explains more alternatives for distribution function (Vensim Documentation, n.d.). The sample case study used in the simulation experiment indicates a normally-distributed demand where the order is placed at the site of the retailer per unit O, at certain t time, equations are as follows:

O(t) = maximum coordinat (0, IO(t))

IO(t) = order rate indicated, that is computed depending on the following three factors:

- The stock (L) losses expected

- The discrepancy between the actual stock (AS) and the desired

- The discrepancy between the actual supply line (ASL) and the desired

Therefore the equation of the order rate is:

IO(t) = Forecast of Demand + gap of actual stock + gap of actual supply line

IO(t) = Forecast of Demand + A•(Safety_level_of_Inventory – (Inv-Backlog(t)) – B•Supplylinegap(t)

The inventory buffer used in the case study is 10000 units which are stored as finished products by the producer. The vendor keeps a stock about 10 tonne. The order is passed from the retailer in the supply chain downstream to the distributor, the wholesaler and the producer upstream. There is a time delay between orders and shipments from one stage to the next, which is approximately one week depending on the sample case and denoted by the FIXED DELAY function.

Ordered= DELAY FIXED (placed, 1, 200) …. (2)

Other discrete DELAY function can be used according to applied case (DELAY INFORMATION function, SMOOTH function, SMOOTH3 function and SMOOTH N function). In the case study, the decision makers used to include a margin of safety in each order located to overcome material misuse during the production cycle. Most of industrial zones in developing countries used to order safety margin to avoid price fluctuation and production deficiencies as discussed in Table 1 - Procurement & Inventory replenishment issues. Therefore, a margin of safety is indicated in the order of material by each player and conversion of unit is being used while ordering supplies. The order amount of finished product is converted into supplies while a producer placing an order to the vendor’ factory. In turn, the amount of modules/components is translated as well into raw materials supplies to that shall be commanded from its suppliers.

For reality imitation in production cycle, the traditional beer game has been adapted to represent two levels of the production cycle. The first is the transformation of raw materials into semi-finished components. The second level shows the transformation of the semi-finished components into finished products. In order for each producer to overcome production losses, a margin of safety is indicated. Units utilized in order equations were converted into supplies once the order is placed by the producer to its suppliers. The amount of order thus shows the units of material requested and placed on the site of the next partner. Large inventory volume is one of key obvious issue while partner estimate its maximum level. Industrial zones used to keep large size of inventory to overcome the delay in delivery and suppliers’ dependence. Therefore, it is obvious that players hold much more quantity rather than needed as discussed in Table 1 - Procurement & inventory Activities.

Placed = MAXIMUM (0, SMOOTH (ordered 1, TIME of SMOOTH) + A * (10000 - (Inventory of Finished Textile - Textile Backlog) – B * Supply Line 2)) ….….. (3)

Supplies are being ordered to replenish inventory buffer. Most of industrial sector of developing countries under exploration ignore the delay in material which may happen at delivery (Khalifa et al., 2008). From decision maker perspective’s, a large buffer of safety can overcome any delay as deliberated in Table 1 - Procurement & Inventory replenishment issues.

For the sample case study used, the delivery of materials may vary from one to two weeks. It relies on the stock available in the warehouse of the vendor. Supply movements are shown quantitatively in the form of a flow linking two stocks, a semi-finished stock at each supplier site and a raw material stock at the customer site. The rate of supply is represented by DELAY MATERIAL, which keeps the material back in time when the delay time varies. It is a discreet function of delay that is having the characteristic of conserving the quantity (Vensim documentation, n.d.).

Supplies = DELAY MATERIAL (ordered 2, Procurement Time, 10, 0) …. (4)

The delivery duration affects the supply rate. Durations of delivery were tested and they were uniformly distributed at random.

Time of Procurement= RANDOM UNIFORM (1, 2, 0.05) …… (5)

The new design of beer game imposes raw material stock in each production cycle because of its significance. Furthermore, the process of production is a transformation of raw materials; therefore, the stock of raw material should be existent in order to articulate the process of production. Since the process of production embodies a transformation from the stock of raw material to the stock of final product, the process of production process is demonstrated by a flow linking the two stocks (inventory of raw material and inventory of final products) at each level of production. Production entry is identified by the difference between the demand (total of backlog/unmet orders and orders of customers with the margin of safety) and the obtainable quantity of inventory (orders delivered and obtainable quantity of inventory). An IF THEN ELSE statement is utilised to make this comparison.

Prod in 2= IF THEN ELSE (Inventory of Finished Textile < (ordered 1 + Backlog of Textile + (ordered 1 * level of safety level)), ((ordered 1 + Backlog of Textile + (ordered 1 * level of safety)) – Inventory of Finished Textile)\ *0.001, 0) …. (6)

Most of equations used to indicate production cycle specifies unit transformation to semi-finished or finished products. The time of production is not assumed to be permanent stationary one as in the traditional game. Time estimated in the proposed beer game depends on production capacity of each producer and considers limited labour skills. Consequently, a long operation has a negative effect on the cost and led to deficiency of production that had been discussed in Table 1.

Time of Production = Size of Production/Capacity of Production …. (7)

Furthermore, the size of production is decremented with the loss of material during the cycle of production at both levels.

Production size= (Prod in - Production Loss) / 0.001 …. (8)

Concerning the production, a FIXED DELAY is used to indicate the duration of production at each level.

Prod = DELAY FIXED (SMOOTH (Size of Production, Time to Adjust Production), (Prod in / Capacity of Production), SMOOTH (Size of Production, Time to Adjust Production))…. (9)

The needed time for machinery adjustment and production is taken into consideration in the production equation. The SMOOTH function is applied to demonstrate that the production of the factory is delayed from the one desired with a time of adjustment, which is hindered by limited labour skills. Mostly, the margin of safety is generated additionally to the ordered quantity to prevent the misuse of material during the production (Khalifa et al., 2008). The units of raw material are converted into the units of semi-product/finished product units for the representation of the transformation and production process. The finished product delivery in downstream is denoted with a one week delay DELAY FIXED function according to the sample case study.

Inflow = DELAY FIXED (sold 0, 1, 200) …. (10)

Equations used for incoming flow and the accumulation of the supply line accumulation mimic the traditional beer game.

Supply_Flow = placed -in …. (11)

The same is applied to the backlog stock of the partner (unmet order accumulation) and its incoming flow.

Textile_Backlog= INTEG (TextilebFlow, 0) …. (12)

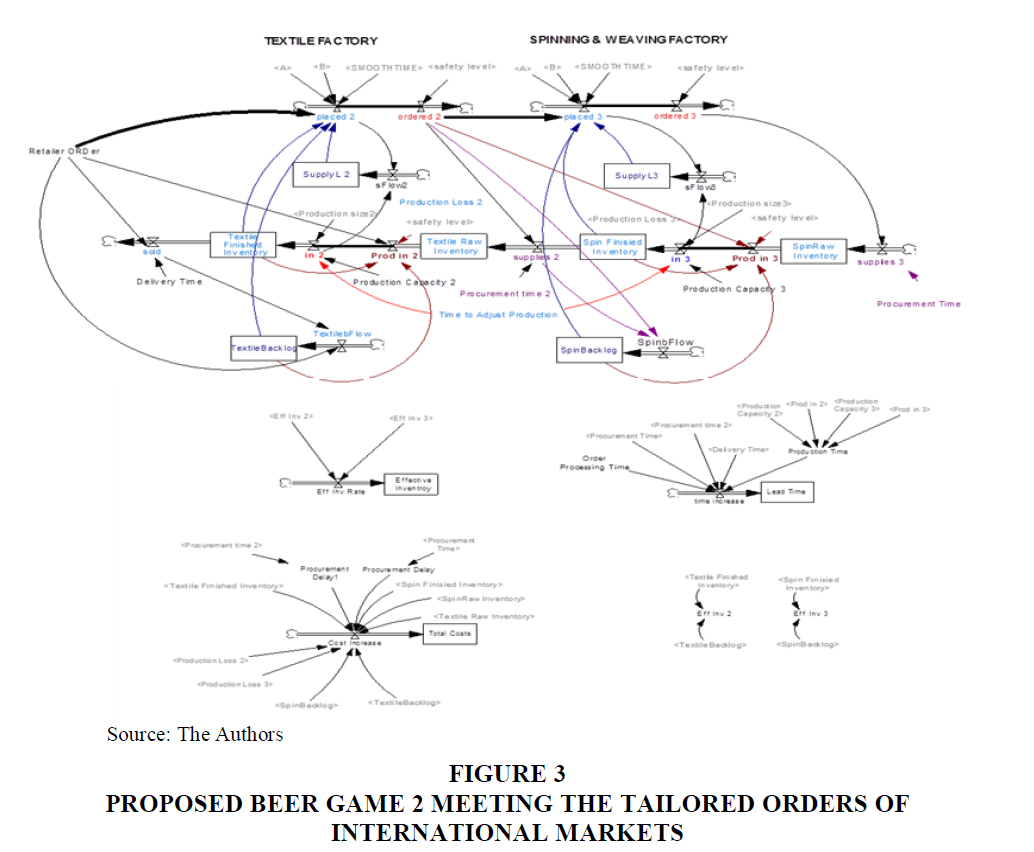
The second proposed beer game is the case of the provision of customised products to international markets (Proposed Beer Game 2) as shown in Figure 3. This model displays the industrial firms’ role as Original Equipment Manufacturers (OEMs) in developing countries. The second proposed beer game is alike to the first one apart from few details. Intermediaries do not exist between producers and international retailers; in this case, direct marketing is used to access international markets. As a result, distributors and wholesalers are excluded from the beer game. The beer game makes a simulation to the producers’ role in meeting an international retailer’s demands, irrespective of the retailer’s role.

For the simulated case, the order of the retailer is distributed normally so that the RANDOM NORMAL function is deployed. RANDOM NORMAL (m, x, h, r, s) offers a normal distribution of mean 0 and variance 1 before it is shifted, extended and truncated, which is equal to a normal distribution of mean h and standard deviation r. The r units match m, x and h (Documentation of Vensim). The experiment begins by placing the orders of the retailer in the OEM unit then placing this order in the manufacturing units:

ORDER of Retailer = RANDOM NORMAL (5718, 272878, 100017, 75667, 0) …. (13)

The producer takes more time in estimating the production’s feasibility of such order in accordance to the availability of resources. The delay in the retailer order’s receipt and its placement to production units is estimated with five weeks. A planning phase would take place to estimate the feasibility of producing customized product insight of supplies required, machinery available, quality constrains pre-defined and cost estimated linked to the cycle of production. The producer locates an order in regards to the factory pre-stating certain constraints for the production cycle.

Placed 3= MAXIMUM (0, SMOOTH (ordered 2, TIME of SMOOTH) + A*(10 - (Spin Finished Inventory – Backlog of Spin) – B * Supply Line3)) .….(14)

Because of the quality constraints pre-defined and imposed by the international retailers and the fact that many supplies are being imported, producers are being faced with long delivery time.

Time of Procurement= RANDOM UNIFORM (1, 8, 2) ….(15)

The factory supplies the manufacturers/producers with semi-finished materials. Delivery of procurement is between 1-2 weeks based on the availability of stock and the delays in production of the simulated case.

Time of Procurement 2= RANDOM UNIFORM (1, 2, 0.5) …(16)

The producer fabricates the requested order and stores it for delivery. Delivery duration is subjective to chosen method for overseas shipment. For our case, it is estimated to be 1- 8 weeks based on final destination.

Sold= DELAY MATERIAL (ORDER of Retailer, Time of Delivery, 500, 0) …(17)

The production cycle of each producer is represented as follows:

Prod in 3= IF THEN ELSE (Spin Finished Inventory < (ordered 2 + Spin Backlog + (ordered 2*Level of Safety)), ((ordered 2 + Spin Backlog + (ordered 2*Level of Safety)) - Spin Finished Inventory), 0) …(18)

in 3= DELAY FIXED (SMOOTH (Size of Production 3, Time to Adjust Production), (Prod in 3/ Capacity of Production 3), SMOOTH (Production Size 3, Time to Adjust Production))..(19)

For Supply line and backlog equations, equations are illustrated as follows:

Supply L 2= INTEG (sFlow2, 200) …(20)

sFlow3= placed 3 -in 3 ….(21)

From the above discussion of the proposed design, it is obvious that the individual decision-making patterns are used by each partner for ordering and replenishment (Ad-hoc pattern). Strategies and decisions trailed for replenishment and size of inventory sometimes signify conflicting objectives and this emphasize more on the non-existence of the pre-defined design of the supply chain and the integrated platform of the supply chain that was discussed in Table 1. Manual techniques are being used for passing orders to next partner, which cause more order delay- Table 1 - Technological aspects. Limited automation technique and IT capabilities are being used which contribute positively to order delay. Lack of information visibility along the chain led to decentralized pattern of decision making for forecasting, procurement and inventory replenishment. Most of these aspects, which have been listed in Table 1, are considered in the proposed Beer Game design to reflect current deficiencies of supply chain activities.

To conclude, the proposed Beer Game contribution takes into account:

1. Constraint on production capacity at the level of production;

2. Loss of material during production processes;

3. Two inventories (raw material and finished product stocks) at each level of production;

4. Delays in the delivery of procurement at production level;

5. The time needed to adjust for the production of customized products;

6. Margin of safety for input production to prevent loss of material;

7. Sales opportunities that are lost and triggered by the delay in material and consequently delay in production;

8. Conversion of units from finished products to raw materials.

The proposed beer game includes added factors of supply chain to indicate a customisation approach. The modified beer game reflected more measurements of performance other than the traditional one did as below:

Total Cost of Supply Chain

A cost measure was used by Sterman's beer game in order to designate the performance of the supply chain. The main objective of the classic beer game is to minimise the costs of the supply chain while preserving a reasonable inventory that enables incoming orders to be fulfilled. The proposed beer game includes a cost measure as well but with different type of measurement. The total cost comprises inventories holding costs (inventories of raw material and finished product), stock-out cost; loss of material cost and lost opportunities for sales, which are measured in the modified beer game on the basis of delay in procurement. Any material delay after estimated duration of delivery for local supplies and outsourced one would be considered in the estimation of cost as sales opportunity that was lost. Therefore, IF THEN ELSE equation is used to check if the delivery time exceeds estimated values. The holding cost is thought of to be half the stock-out cost as presumed in the model of Sterman (Sterman, 1989; Kirkwood, 1998).

Effective Inventory

This denotes the most inventories available for each partner. These are the differences between the amount of inventory and the backlog (accumulation of unmet orders) at each supply chain level. Effective inventory measure is deployed for the control of the responsiveness level to the orders of customers. Effective inventory is measured at each supply chain stage and accumulative effective inventory along the chain is specified as another measure for the performance of the supply chain.

Lead Time

Order-to-Delivery lead time is the elapsed time between the order placement of the customer and its delivery. It contains lead time of the supplier, lead time of manufacturing, lead time of distribution, and time of order management. The lead time is used as a performance indicator in the modified beer games because of its effect on the supply chain performance. The lead time is a crucial factor in make-to-order supply chains. Lead time is correlated with the levels of inventory, customer service, and costs. The reduction in lead time will boost a decision maker to maintain a slight buffer while the firm is capable of meeting a wide range of customer requirements (Hwarng & Xie, 2006). This will result in the improvement of the order responsiveness that is obligatory in the adoption of the mass customisation. Lead time is utilised to estimate the needed time for the receipt of an order allocated by the retailer.

Simulation Beer Game Outcomes

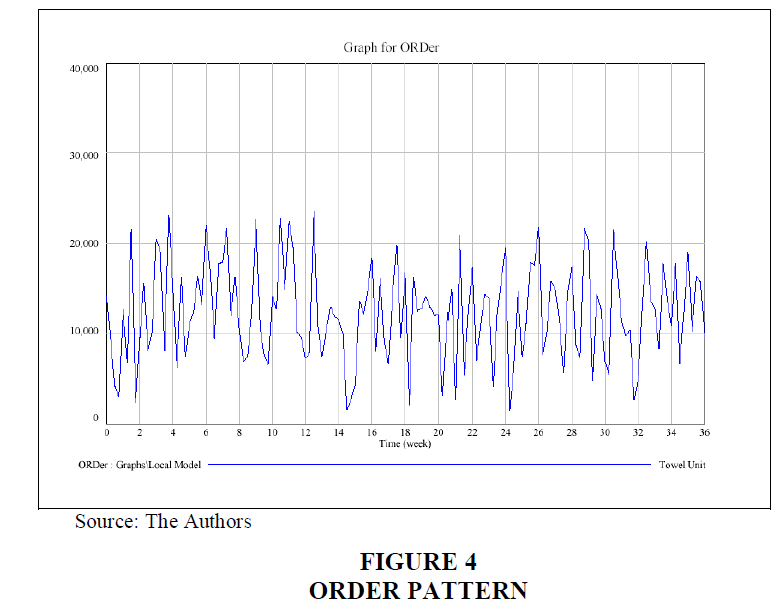
The simulation remained for 36 weeks, which is the typical time period applied in Sterman‘s game. The outcome verifies that the order of the customer/retailer is being augmented while going forward along the supply chain. Figure 4 shows the output of the experiments. This demand pattern’s augmentation is clear especially in the experiment of the first proposed beer game. The reason behind that is the effect of bullwhip that makes demand signals’ distortion when passing across the chain causing such augmentations. Many studies have referred back the effect of bullwhip to the lack of information visibility and the long lead times through the supply chain (Hwarng & Xie, 2008; Größler, 2020). Orders allocated by the producers to their vendors showed the same increased pattern. The cause for this is the conversion of order units into supplies demanded from the vendor to control the cycle of production.

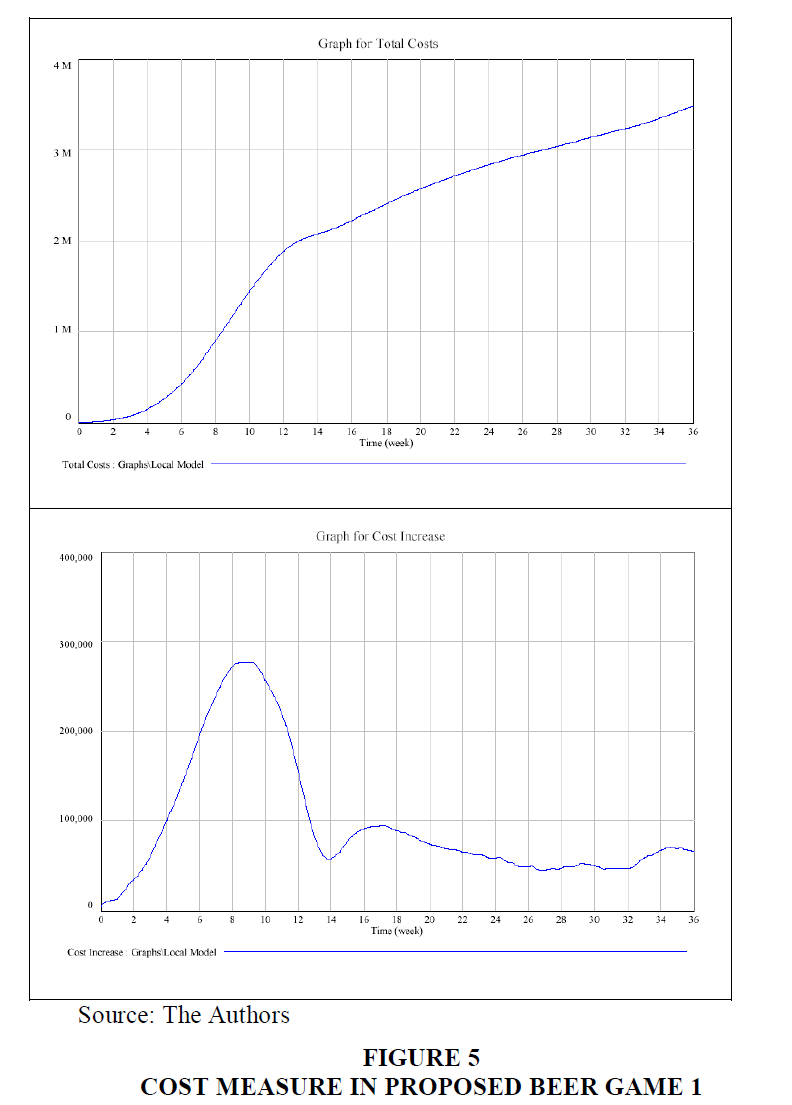
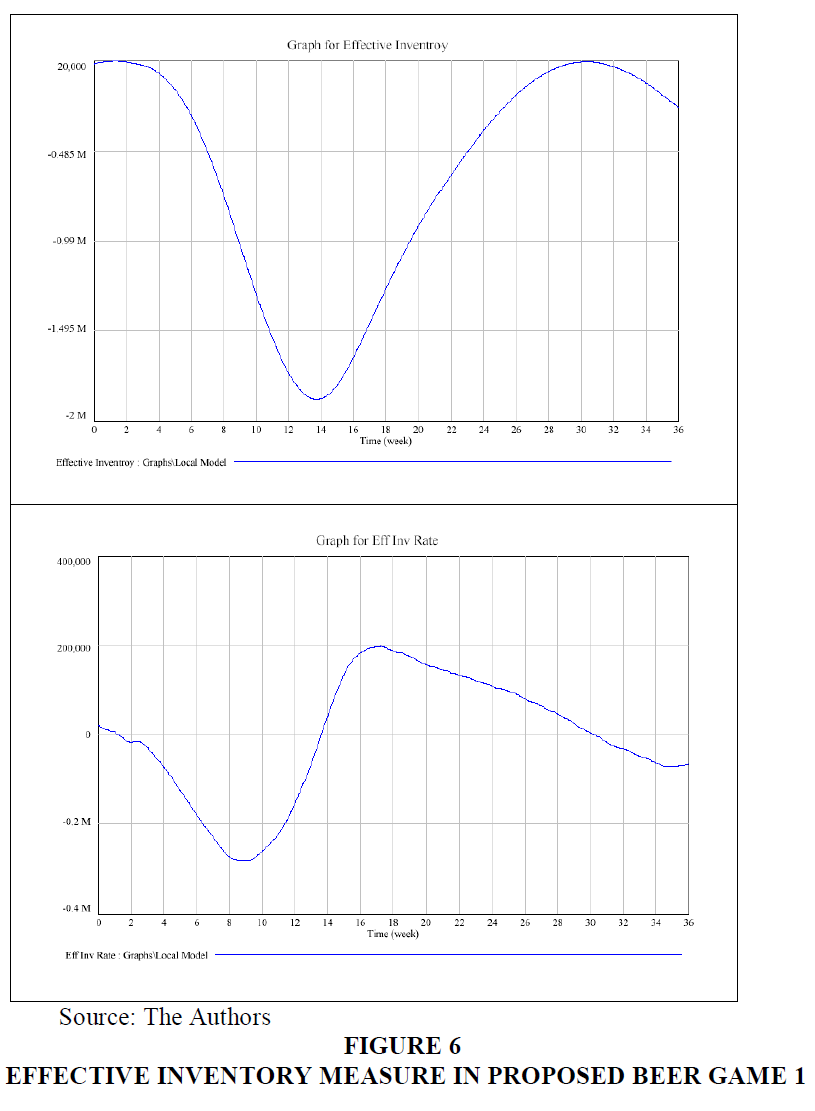
In accordance to cost measures, the total cost of the chain increases exponentially over the course of 36 weeks in both experiments. The outcome of the experiment of the Proposed Beer Game 1 was demonstrated in Figures 5 & 6. It indicates that the cost rate increases rapidly till week 9, the increase in the rate is due to a clear drop in effective inventory over the chain. The effective fall in inventories refers to the large backlog of inventories of textiles and raw materials during the same period, coupled with a high loss in production. By week 17, the cost rate will gradually decline, with only a small increase by week 32. This pattern is coupled simultaneously with effective inventory reduction. The cause for this is that textile backlog and loss rates in production occur at their minimum levels and indicate an increase in the simulation over the last few weeks. In addition to the textile inventory, raw material buffer at each level of production is sufficient to meet the needs of the partner until week 32, when they demonstrate a further fall.

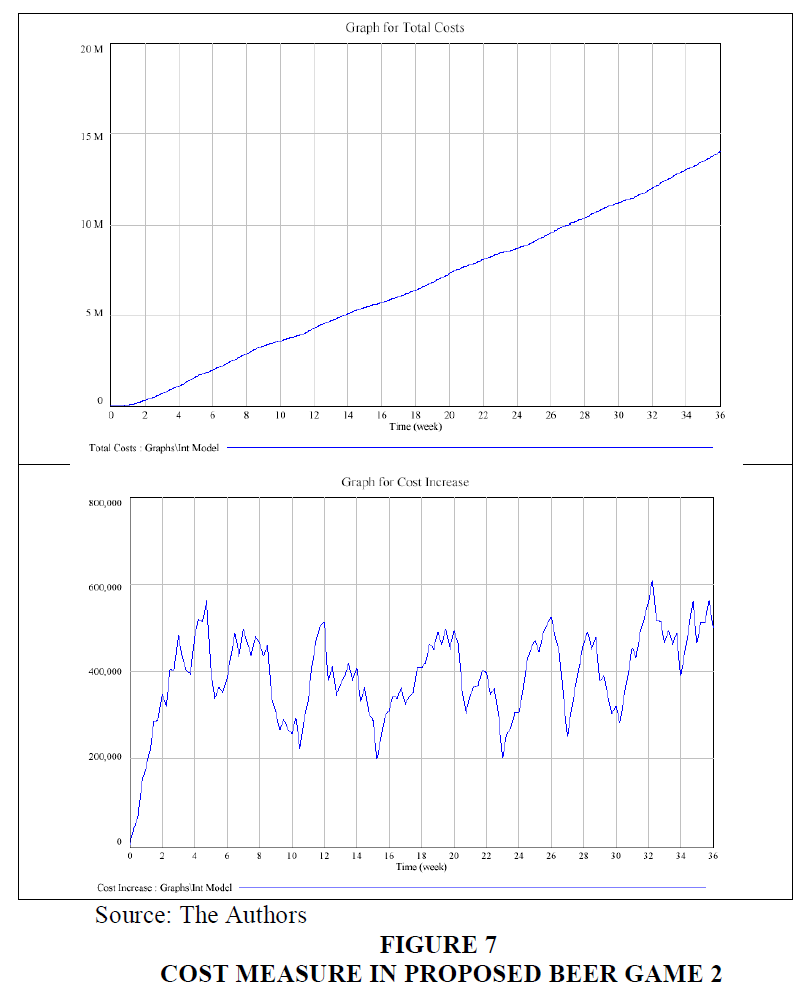
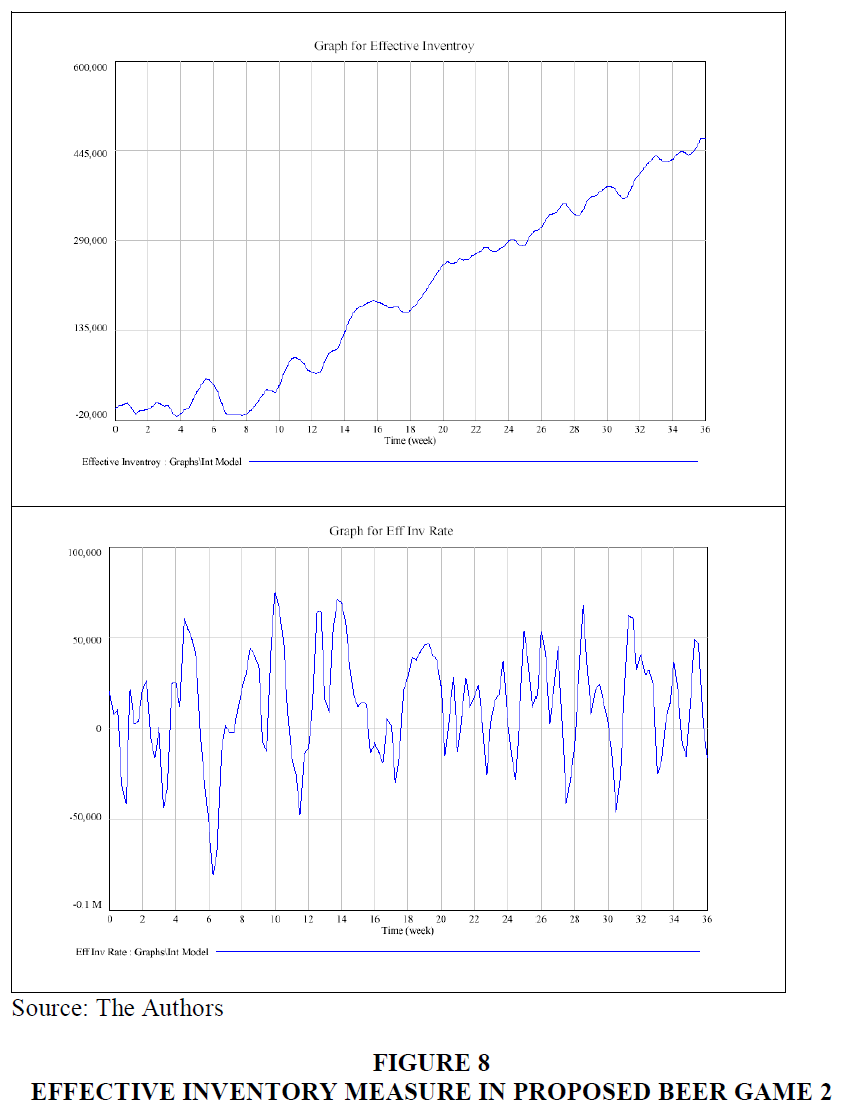
For the experiment of the second Proposed Beer Game 2, Figures 7 & 8, exhibit the system behavior and the performance measure. The cost measure oscillates over the time of the experiment. This pattern is in conjunction with a fluctuating rate of effective inventory over the course of the experiment. Variations in textile inventories and backlogs of textile fabrics are the principal reason of oscillating production losses and fluctuating delivery delays for local and overseas supplies. Delays for outsourced supplies might be up to 4 weeks, while restricted to local supplies.

Conclusion

The study results constitute with a generic design of a beer game which considers the deficiencies of supply chain in developing countries. Re-designing process of beer game was based on a cross-industry field study and did not rely on simple assumption that could not imitate the real situation of OEM industrial firms. The proposed design of beer game overcomes constrains assumed by Sterman’s design and represent real difficulties face supply chain activities. Since there exist a number of factors that impact the performance of the supply chain leading to non-linearity in the system, the new design of proposed beer game consider most of these factors that are linked to the external environment for instance delivery issues and country infrastructure which cannot be considered as controlled factors by industrial zones in developing countries, other factor related have been considered in the proposed beer game design such as: limited production capabilities, labour skills, material loss during production cycle, machinery adjustment time to produce customized products and order safety margin to avoid material loss. Proposed Beer Game considers as well the unit conversion from finished products to raw materials in ordering and stocking equations. For mmeasuring supply chain performance, cost cannot be the only measure to rely on, a combination of lead time, effective inventory and cost measures are being adapted in the proposed beer game to indicate a comprehensive performance measurement. The design of Proposed Beer Game presents a generic one which can be used in simulating any industrial sector in developing countries. Running a simulation model driven from real dataset will impose more realistic simulation experiments in order to propose appropriate solutions.

References

1. Abt, C.C. (1970). Serious games. New York: Viking.
2. Andersen, D.F., Chung, I.J., Richardson, G.P., & Stewart, T.R. (1990). Issues in designing interactive games based on system dynamics models. In Proceedings of the 1990 International System Dynamics Conference (Vol. 1, pp. 31-45). Chestnut Hill.
3. Anderson, J.C., Håkansson, H., & Johanson, J. (1994). Dyadic business relationships within a business network context. Journal of Marketing, 58(4), 1-15.
4. Beamon, B.M. (1998). Supply chain design and analysis:: Models and methods. International Journal of Production Economics, 55(3), 281-294.
5. Crooltall, D., Oxford, R., & Saunders, D. (1987). Towards a reconceptualization of simulation: From representation to reality. Simulation/Games for learning, 17(4), 147-71.
6. D’Atri, A., & Motro, A. (2009). Virtual enterprise transactions: a cost model. In Information systems: People, organizations, institutions, and technologies (pp. 165-174). Physica-Verlag HD.
7. EgyTex. (2009). Official Portal of Egyptian Textile industry, “Egyptian Cotton Dilemma Still Unresolved”. Available at: http://www.egytex.com/researches/industryreports
8. Ellington, H., Addinall, E., & Percival, F. (1982). A handbook of game design. Kogan Page.
9. Forrester, J.W. (2005). System dynamics and the lessons of 35 years-a chapter for the systemic basis of policy making in the 1990s-Massachusetts Institute of Technology–Abr. 1991.
10. Forrester, J.W. (2009). System dynamics: The classroom experience: Quotations from K-12 teachers. Unpublished manuscript, Massachusetts Institute of Technology (MIT), Cambridge, MA.
11. Größler, A. (2020). System dynamics and operations management. System Dynamics: Theory and Applications, 273-284.
12. Hwarng, H.B., & Xie, N. (2008). Understanding supply chain dynamics: A chaos perspective. European Journal of Operational Research, 184(3), 1163-1178.
13. Joshi, Y.V. (2000). Information visibility and its effect on supply chain dynamics. Unpublished doctoral dissertation, Massachusetts Institute of Technology.
14. Khalifa N., White A., & El Sayed A. (2009). Supply chain difficulties facing Egyptian fabrics reaching global markets: A beer game simulation. The third International Conference on Operations and Supply Chain Management, Wuhan.
15. Khalifa, N., White, A., & EI Sayed A., (2008). Supply chain challenges in developing countries: Cross industry case studies, cybernetic intelligent systems. Proceedings of 7th IEEE International Conference- Pages: 145-152, Middlesx-UK.
16. Kimbrough, S.O., Wu, D.J., & Zhong, F. (2002). Computers play the beer game: can artificial agents manage supply chains?. Decision Support Systems, 33(3), 323-333.
17. Kirkwood, C.W. (1998). Business process analysis workshops: System Dynamics Models. Chapter 4: The Beer Game. Arizona State University.
18. Klabbers, J.H. (2003). The gaming landscape: A taxonomy for classifying games and simulations. In DIGRA conference (pp. 4-6).
19. Kopainsky, B., & Sawicka, A. (2011). Simulator?supported descriptions of complex dynamic problems: experimental results on task performance and system understanding. System Dynamics Review, 27(2), 142-172.
20. Lajili, K., & Mahoney, J.T. (2006). Revisiting agency and transaction costs theory predictions on vertical financial ownership and contracting: Electronic integration as an organizational form choice. Managerial and Decision Economics, 27(7), 573-586.
21. Lee, H.L., Padmanabhan, V., & Whang, S. (1997). The bullwhip effect in supply chains. Sloan management review, 38, 93-102.
22. Maier, F. H., & Größler, A. (2000). What are we talking about?—A taxonomy of computer simulations to support learning. System Dynamics Review: The Journal of the System Dynamics Society, 16(2), 135-148.
23. Martinez, M.T., Fouletier, P., Park, K.H., & Favrel, J. (2001). Virtual enterprise–organisation, evolution and control. International Journal of Production Economics, 74(1-3), 225-238.
24. Ming, D. (2001). Performance analysis and configuration simulation in integrated supply chain network design.
25. Mohaghegh, M., & Größler, A. (2020). The dynamics of operational problem-solving: A dual-process approach. Systemic Practice and Action Research, 33(1), 27-54.
26. Perera, H.N., Fahimnia, B., & Tokar, T. (2020). Inventory and ordering decisions: a systematic review on research driven through behavioral experiments. International Journal of Operations & Production Management.
27. Sterman, J.D. (1989). Modeling managerial behavior: Misperceptions of feedback in a dynamic decision making experiment. Management science, 35(3), 321-339.
28. Vensim Documentation. (n.d.). Retrieved from http://www.vensim.com/documentation/
29. Williamson, O.E. (1981). The economics of organization: The transaction cost approach. American Journal of Sociology, 87(3), 548-577.
30. Yang, F., Huang, J., Feng, X., & Yang, M.M. (2020). Decision-making in a dynamic task: Effects of goal orientation on stocks and flows performance. Chinese Management Studies, 14, 695-713.