Research Article: 2019 Vol: 18 Issue: 5
Multivariate Discriminant Analysis Managing Staff Appraisal Case Study
Muwafaq AlKubaisi, University of Bahrain
Waleed A. Aziz, University of Bahrain
Shaju George, University of Bahrain
Khaled Al-Tarawneh, University of Bahrain
Abstract
Keywords
Data analysis, Regression Analysis (RA), Dependent Variable, Interval Variable, Nominal Variable, Discriminant Analysis (DA), Predictive Validity.
Introduction
Many situations we are faced with the question of what sort of analysis to use in a specific situation. Many situations, the regression analysis method is considered one of the utmost robust analyses tool when we are involved in forming relationships. An essential assumption of the RA technique is that the dependent variable (Y) must be an interval variable. If this assumption is violated, then, RA is no longer appropriate. For example; we want to forecast and differentiate between Male and Female GPA score for students registered at a specific college. Because the dependent variable has a nominal scale with two categories: Male=1 and Female=2. As a result, the RA will not be appropriate in this situation. Therefore we have to revert to discriminant analysis (DA) as we have a nominal variable (Fernandez, 2002).
DA is a parametric technique to govern which weightings of independent variables are best to differentiate (discriminate) between 2 or more categories of cases and do significantly better than chance (Cramer, 2003). The analysis generates a discriminant function, which is a linear combination of the weightings and scores on these variables. The maximum number of functions is the minimum number between number Independent Variables and the number of data groups minus one.
The primary hypothesis for a DA is that the sample data follow the normal distribution, whereas LR is called a distribution-free test with no need for normality assumption. The parametric tests are very potent comparing with the non-parametric alternative (Ramayah, 1970; Ramayah et al., 2004).
The discriminant functions (DF) are made to exploit the differentiation between the groups. The discriminant coefficients can assist in recognizing which variable(s) have more contribution to differentiate about the corresponding dimension. Significant independent variables typically have to higher weights.
A set of classification functions can be derived once a group of variables is found which can form acceptable discrimination for the data cases with known group memberships. These functions can be applied to new cases with unknown memberships.
Overview of Discriminant Analysis
The term DA (Fisher, 1936; Lohnes, 1971; Gnanadesikan, 2011; Klecka et al., 1980; Hand, 1981; Silverman, 1986) refers to numerous types of analyses. DA is used to categorize observations into two or more of known groups based on one or more quantitative variables (Inc, 2016).
The researcher picks a group of discriminating variables that quantity attributes in which the groups are anticipated to vary from one group to another. It is beneficial for circumstances where a researcher wishes to build a model of group membership based on observed characteristics of each data case. The practice generates a DF (or a set of DFs’) based on linear combinations of the independent variables.
To estimate the number of DF’s we select the smaller number between the number of independent variables and the number of controlling variables -1. We should understand that the emphasis of the analysis is not to forecast but to clarify the association between data cases. DA basically, selects variables (from list of variables) that can differentiate between groups and produce the smallest error of classification when used as a tool of discrimination. The DA tries to do select variables by creating one or more linear combinations of the DV’s.
The typical DF can be written as follows:
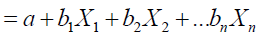
Where: Di= DF or the predicted score
bi = the discriminant coefficient or weight for that variable i
Xi = the independent score for independent variable i
a = a constant
n = the number of independent variables
The major DA assumptions include:
i. The collected sample is random;
ii. Independent variables must follow a normal distribution;
iii. Responses for the dependent categories must be classified correctly;
iv. For the dependent variable, several groups or categories must be at least two mutually exclusive.
V. groups or categories must be defined before collecting the data.
The assumptions mentioned above will be discussed in more details when we come to analyze the case study data.
Research Problem Case Study
The case study of interest is about a group of engineers operating in the national construction company in Iraq. The population frame is defined as all engineers working for this company with a minimum of one year experience. The company administrators have been observing that some engineers perform more effectively compared to others. From the literature review, four variables that can be recognized as probable discriminators; these include job history to assess the experience; job test to evaluate knowledge in engineering; and a personality measure that assesses friendliness; and finally college GPA to appraise their performance at college. The research is interested in determining whether these four scores (predictors) are useful in predicting job performance (dependent variable). One-hundred-and-fifty applicants are hired and worked for the firm for one year or more. At the end of the year, a board appraises the engineers and classifies them into one of 3 categories: a poor performer (=1), good individual achiever (2), or a good team player (=3). Data have been analyzed using SPSS package on data file of 150 cases and five variables, the four predictor variables, and grouping variable distinguishing among the three job performance groups.
The research attempts to assess the influence of the independent variables (predictors) mentioned above on job performance task in any organization. Figure 1 shows the research working model, which will be further investigated. Our application has three groups and four quantitative variables. Consequently, the number of functions is two because 2 is the minimum of the two values, (number of groups =3-1=2), and (number of predictors =4). The first discriminant function is produced in a way that it maximizes the variances on this function among groups. A second discriminant function may then be extracted that maximizes the differences on this function among groups but with the added restriction that it is uncorrelated with first discriminant function. The additional discriminant function may be produced that maximize the variances among groups but always with the constraint that they are unassociated with all formerly extracted functions.
Eigenvalues associated with DF’s indicates how well the functions differentiate the groups. A higher value of the “eigenvalue” means better discriminating the groups.
An “eigenvalue” for a DF is the fraction of the “between-groups sums of squares” to “the within- group sums of squares” for an ANOVA that has the discriminant function as the dependent variable and groups as levels of a factor (Stevens, 2002). Because eigenvalues reflect how well the function discriminate the groups, the biggest eigenvalue is connected with the first discriminant function; the second main eigenvalue is related to the second DF and so on. These linear combinations of predictor variables are named Fisher’s linear discriminant function by SPSS package, and their coefficients are denoted to as Fisher’s function coefficient. Accuracy in classification is appraised by computing the percent of cases appropriately predicted into groups based on the classification functions. An alternative statistics, “Kappa” also evaluates the percentage of cases correctly classified except that it corrects for chance agreements.
Interpretation of DF Coefficients
The SPSS computer package will typically yield eigenvalues, Wilks’ Lambdas, and beta coefficients. The standardized DF coefficients are of immense logical importance; they offer an indicator of the importance of each independent variable. The sign on the coefficients (±) specifies the type of the relationship, whether the variable is making a positive or negative influence. Coefficients with large absolute values associated with variables have more excellent differentiating capability. The Structure Matrix Correlations are generally used in the statistical analysis as they offer more precise values than the Standardized Canonical DF Coefficients. The structure matrix, which shows the correlations of each variable with each DF, is tabulated. These Pearson coefficients are structure coefficients and serve like the cut-off between significant and less significant variables. The most substantial loadings for each discriminate function determine how each function is to be named (McLachlan, 2004). The DF coefficients b (standardized form beta) also denotes the “partial influence” of each independent variable to the DF controlling for all other variables in the equation (Chen & Hung, 2010). They evaluate each independent's variables’ unique influence and also provide information on the relative importance of each variable (Burns & Burns, 2008). Wilks' lambda function is to measure how well each function separates the data into groups. If the values of Wilks lambda small, this would indicate it has a high ability to differentiate the function. The value of chi-square will test the equality of all means of the functions listed across groups (Hair et al., 2010).
Using the SPSS Computer Package in the Data Analysis
To start with the DA, we need to select the Grouping Variables which splits the data file into two or more groups then we have to “define range” the categories of your grouping variable which will specify the minimum and maximum integer for the number of the grouping variable. For the case study used for this analysis, the range was between 1, 3. We have to select Independent variables which we should select at least one independent variable to run this technique. In our case study, we have four predictors: Friendliness, College GPA, Job Record, and Profession Test.
Testing Normality of the Predictor's Variables
First, we check whether the Sig. Values of Shapiro-Wilk less the 0.01 Significance level for the test (consider Table 1). Although 2 of the four independent variables (Job-record and Profession-Test) are significant, which may appear that these two variables are not normally distributed (rejecting H0 of normality). Therefore, we can use another method to test the normality of all dependent variables. We need to calculate the standard value of the normal distribution (Z) for Skewness & Kurtosis coefficients by dividing each statistic by its standard error using the Descriptive results in Table 2. If the calculated Z is within the value of ±1.96, then the H0 hypothesis will be accepted of normality.
| Table 1 Tests of Normality | ||||||
| Statistic | df | Sig. | Statistic | df | Sig. | |
| College GPA | 0.063 | 150 | 0.200* | 0.984 | 150 | 0.085 |
| Friendliness | 0.069 | 150 | 0.078 | 0.992 | 150 | 0.546 |
| Job Record | 0.157 | 150 | 0.000 | 0.946 | 150 | 0.000 |
| Profession Test | 0.093 | 150 | 0.003 | 0.972 | 150 | 0.003 |
| Table 2 Summary of Predictors Z-Value | ||||||
| Dependent Variable | Skewness | Slandered Error | Z Value | Kurtosis | Slandered Error | Z Value |
| Friendliness | 0.087 | 0.198 | 0.439 | 0.039 | 0.394 | 0.099 |
| College GPA | -0.012 | 0.198 | -0.061 | -0.692 | 0.394 | -1.756 |
| Job Record | 0.286 | 0.198 | 1.444 | -0.601 | 0.394 | -1.525 |
| Profession Test | -0.262 | 0.198 | -1.323 | -0.426 | 0.394 | -1.081 |
From the Table 2 above, we can notice all z values for skewness and Kurtosis fall within the range ±1.96. Therefore we can conclude that, regarding skewness and Kurtosis, the data are little Skewed and Kurtotic for all independent variables, but not differ significantly from normality. We can assume that our data are approximately normally distributed with regarding skewness and Kurtosis.
Testing Predictors if they have Outliers
Now As far as outliers, if we consider the four box plots of all variables have no points plotted below the bottom whisker, nor above the top whisker, so we assumed that we do not have outliers all predictor variable. Consider Figure 2.
As far as outliers, we will consider the four above box plots. The first one is college GPA, we have no points plotted below the bottom whisker or above the top whisker, so we assumed we do not have outliers then we check the rest of predictor variables, and obviously. It looks; obviously, none of them has outliers; therefore, we have met the no outliers exist in the data.
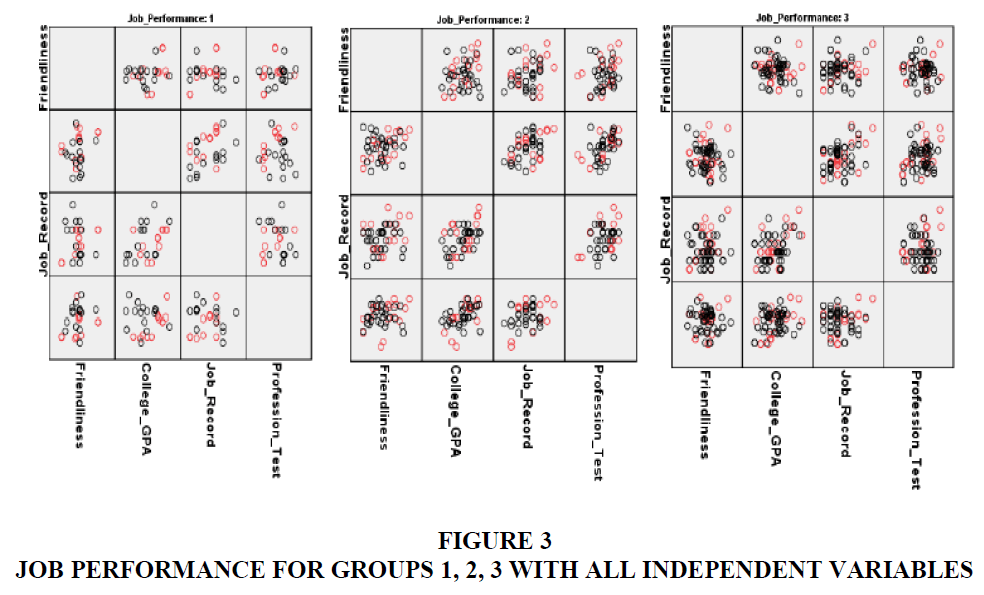
Testing Linearity of the Relationships of Predictors Group
For the sake of performing this test, we need to split the data to organize the data into three groups related to the dependent variable (Job Performance). The three graphs below show the output of breaking the data as follows (consider Figure 3).
The research paper adopted the matrix scatter, in SPSS to do the linearity judgment. These graphs show more or less some linearity pattern between most of the pairs of groups of the dependent variable.
Testing there is no Multicollinearity
We need to perform a correlation matrix and consider the correlation coefficients for all predictor variables. There are a few definitions of multi collinearity, but in general, if the values are below 0.8 or 0.9, the assumption is considered satisfied.
The maximum correlation value From Table 3 below, is 0.45, which is well below 0.8. Therefore we consider the multi collinearity assumption is met.
| Table 3 Correlations Matrix | |||||
| Friendliness | College GPA | Job Record | Profession Test | Friendliness | |
| Friendliness | Pearson Correlation | 1 | 0.057 | 0.114 | 0.087 |
| Sig. (2-tailed) | 0.486 | 0.163 | 0.291 | ||
| N | 150 | 150 | 150 | 150 | |
| Friendliness | Pearson Correlation | 0.057 | 1 | 0.450** | 0.405** |
| Sig. (2-tailed) | 0.486 | 0.000 | 0.000 | ||
| N | 150 | 150 | 150 | 150 | |
| Job Record | Pearson Correlation | 0.114 | 0.450** | 1 | 0.214** |
| Sig. (2-tailed) | 0.163 | 0.000 | 0.008 | ||
| N | 150 | 150 | 150 | 150 | |
| College GPA | Pearson Correlation | 0.087 | 0.405** | 0.214** | 1 |
| Sig. (2-tailed) | 0.291 | 0.000 | 0.008 | ||
| N | 150 | 150 | 150 | 150 | |
The Sample Size Required for the Analysis
Regarding sample size, we should have five times as many observations as predictor variables. In our case, we have five predictor variables and 150 observations, so we have met that assumption as 150> 5*5=25.
The Discriminant Analysis
First step in DA is to test the equality of means. Consider the following Table 4.
| Table 4 Tests of Equality of Group Means | |||||
| Variables | Wilks' Lambda | F | df1 | df2 | Sig. |
| Friendliness | 0.896 | 8.507 | 2 | 147 | 0.000 |
| College GPA | 0.896 | 8.544 | 2 | 147 | 0.000 |
| Job Record | 0.918 | 6.573 | 2 | 147 | 0.002 |
| Profession Test | 0.772 | 21.647 | 2 | 147 | 0.000 |
All predictor variables have shown significant results at alpha 0.01. Next, we consider the equality of covariance matrix. The result 0.301 shows the insignificant result at alpha 1% or even 5%, which means accepting H0 all populations’ variances are equal, as shown in the Table 5 below. So, we have met the second assumption for using the Discriminant Analysis. Consider Table 5.
| Table 5 Test Results of Equal Variances | ||
| Box's M | 23.867 | |
| F | Approx. | 1.138 |
| df1 | 20 | |
| df2 | 31572.000 | |
| Sig. | 0.301 | |
The Eigenvalues which it has two functions (Number of dependent variable groups-1), when we look at highest eigenvalue, which is 0.397 the highest value of eigenvalue the better it fits (Table 6). Considering Canonical discriminant function, we need to check the parameter of the canonical correlation (r), R2 will give you percentage the variations between the categories have been shown (explained). Significant tests can help determine how many discriminant functions should be interpreted. If overall Wilks Lambda is significant, but none of the remaining functions is significant, only first discriminate function is interpreted. If the first two WILKS Lambdas are significant, but none of the remaining ones are significant, then only the first two discriminate functions are interpreted. In our case, the overall lambda and the lambda after removing the first discriminant function are significant, and both discriminant functions could be explained according to chi-square tests.
| Table 6 Eigenvalues | ||||
| Function | Eigenvalue | % of Variance | Cumulative % | Canonical Correlation |
| 1 | 0.397a | 76.5 | 76.5 | 0.533 |
| 2 | 0.122a | 23.5 | 100.0 | 0.329 |
The first discriminant function has an eigenvalue of 0.397 and the canonical correlation of 0.533. When squaring the canonical correlation for the first discriminant function, we obtain 0.28; we find the “eta square” that would result from conducting a one-way ANOVA on the first discriminant function. This result implies that 28% of the variation of the scores for the first discriminant function is accounted for by differences among the three groups of “Job performance” groups. Therefore, when we square the canonical correlation for the second discriminant function, we get the job performance factor causes 11% of the variability of the scores for the second discriminant function.
When we come to WILKS’ Lambda value vary between 0 and 1 (To test the significance of the model as a whole, we have the following two hypotheses: H0: the three groups have the same mean discriminant function scores μ1= μ2= μ3 V H1: μ1, μ2, μ3; are not all equal). From Table 7, if lambda close to 0, it means there is variation between the groups mean different otherwise if Lambda is closer to 1, it means there are real differences between the groups mean. From the Table 7 of wilks’, it is obvious the value of Lambda for both functions higher than 0.5 and the significance level less than 1%, which will imply that the variations between the three groups significantly different.
| Table 7 Wilks' Lambda | ||||
| Test of Function(s) | Wilks' Lambda | Chi-square | df | Sig. |
| 1 through 2 | 0.638 | 65.388 | 8 | 0.000 |
| 2 | 0.891 | 16.722 | 3 | 0.001 |
The two Tables 8 & 9 below related to the two discriminant functions shows that in the first function the most influential variable is Profession Tests it has the highest coefficient of 0.778 whereas, the second function the most influential variable is Friendliness with a coefficient of 0.894.
| Table 8 Standardized Canonical Discriminant Function Coefficients | ||
| F-1 | F-2 | |
| Friendliness | -0.371 | 0.894 |
| College GPA | 0.187 | -0.281 |
| Job Record | 0.384 | -0.017 |
| Profession Test | 0.778 | 0.404 |
| Table 9 Structure Matrix | ||
| F-1 | F-2 | |
| Profession Test | 0.829* | 0.423 |
| College GPA | 0.540* | -0.061 |
| Job Record | 0.474* | 0.051 |
| Friendliness | -0.195 | 0.909* |
The strength of the relationship is assessed by the magnitudes of the standardized coefficients for the predictor (independent) variables in the function and the correlation coefficients between the predictor variables and the function within a group (coefficient in structure matrix). For the first discriminant function Profession test has a relatively large positive coefficient on the level of standardized function and structured matrix, while for the second discriminant function, the largest positive coefficient is the Friendliness variable. On this basis of these standardized function and structure coefficients, we will name the first and second discriminant functions Profession and Friendliness respectively. To build the DF for the dependent variable about the three categories, we can use the Table 10 below:
| Table 10 Classification Function Coefficients | |||
| Job Performance | |||
| 1 | 2 | 3 | |
| Friendliness | 0.289 | 0.334 | 0.385 |
| College GPA | 10.393 | 10.198 | 9.595 |
| Job Record | 0.344 | 0.532 | 0.205 |
| Profession Test | 0.602 | 0.711 | 0.593 |
| (Constant) | -45.646 | -55.801 | -45.740 |
The group centroid Table 11 can label which category has the highest mean value on each discriminant function for the three groups. In our case, when we link group centroid table with structured matrix table, we have a group (2) got the highest mean of 0.832 which represents the individual achiever group had the highest mean score in the profession test, whereas, the team player group had the highest mean score on the friendliness dimension. This interpretation is consistent with our interpretation of the two functions.
| Table 11 Functions at Group Centroids | ||
| Job Performance | F-1 | F-2 |
| 1 | -0.017 | -0.706 |
| 2 | 0.832 | 0.163 |
| 3 | -0.579 | 0.173 |
The output for group classification is shown in the Table 12 below. The classification results permit us to find how well we can group membership using a classification function. The top part of the Table 12 (labeled Original) indicates how well the classification function predicts in the sample. Correctly classified cases appear on the diagonal of the classification table. The Table 12 displays that only 5 cases out of 29 cases (17.2%) of the first group (were correctly identified, 36 cases out of 50 (72%) were correctly identified, and 59 out of 71 cases (83.1%) were correctly identified. The results in (Table 12) shows how well classification functions predicted the N left-out cases are reported in the cross-validated table. As shown in the cross-validated table, 5 of poor performers, 35 of individual achievers, and 58 of team players were correctly classified. Overall, 65.3% of the cases were correctly classified. About 67% of the overall cases were correctly classified.
| Table 12 Classification Resultsb,c | ||||||
| Job Performance | Predicted Group Results Membership | Total | ||||
| 1 | 2 | 3 | ||||
| Original | Count | 1=Poor Performance | 5 | 9 | 15 | 29 |
| 2=Individual Achiever | 3 | 36 | 11 | 50 | ||
| 3=Team Player | 5 | 7 | 59 | 71 | ||
| % | 1 | 17.2 | 31.0 | 51.7 | 100 | |
| 2 | 6.0 | 72.0 | 22.0 | 100 | ||
| 3 | 7.0 | 9.9 | 83.1 | 100 | ||
This percentage is affected by chance agreement. SPSS package is capable of determining an index called “Kappa”. This index can correct for chance agreements, could be reported in the Results section, along with the proportion of individuals who are correctly classified. Therefore, we will compute Kappa to assess the accuracy in the prediction of a group membership. Kappa is a method for assessing the classification table from the DA. Considering Table 13 displays the output of the Kappa coefficient (0.444), which can be regarded as a moderate accuracy in prediction. Kappa has ranged between ±1, the more it gets close to 1 would indicate to perfect prediction, while a value close to 0 indicates chance-level prediction. A negative value for Kappa indicates poorer than a chance-level prediction, while and coefficient higher than 0 indicate better than a chance-level prediction.
| Table 13 Symmetric Measures | |||||
| Value | Asymp. Std. Errora | Approx. Tb | Approx. Sig. | ||
| Measure of Agreement | Kappa | 0.444 | 0.059 | 7.311 | 0.000 |
| N of Valid Cases | 150 | ||||
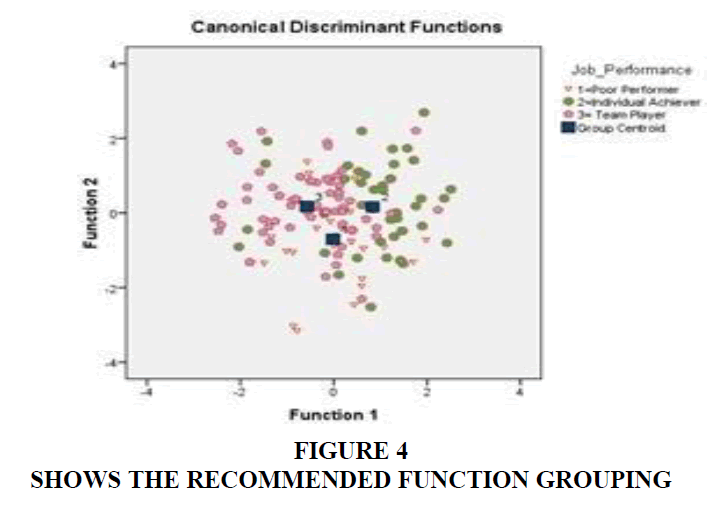
SPSS offers graph outputs which expose the classification of the three groups, as shown in the Figure 4 below for the recommended Function-1.
Conclusion
This paper has offered an illustration on how to perform DA and how the results can be stated and interpreted in a way that is grasped. A discriminant analysis was showed to show whether four predictors (Friendliness, College GPA, Job Record, and Profession Test) can predict Job Performance. The overall Wilks’s lambda was significant, (0.64), χ2=8, N=150) =65.388, p<0.01 indicating that the overall the predictors differentiated among the three categories of the Job performance.in addition, the residual Wilks’s Lambda was significant=0.89, χ2=3, N=150) =16.72; p<0.01. This test indicated that the predictors differentiated significantly among the three groups of “job performance” after distinguishing out the influence of the first discriminant functions. Because these tests were significant, we chose to interpret both discriminant functions.
1. The discriminant function has properly assessed and classifies about 66.7% of the cases that are included in the analysis. 83.1% of the classified cases are classified into the third group (team player), 72.0 % of the classified cases are classified into the second group (Individual Achiever), leaving the first group with 17.2% (Poor Performance).
2. The predictors' “Friendliness” and “Profession Test” have the most contribution in the classification dependent variable Job Performance, where the canonical discriminant function coefficient between function 1 and the professional test is 0.829, so there is a direct relation between the predictor, professional test, and the groups of job performance. Likewise, the canonical DF coefficient between function 1 and the predictor Friendliness is 0.909. This implies that there is a robust direct relationship between the predictor, Friendliness, and the groups of “job performance”.
3. The independent variables Profession Test, College GPA, and Job Record are more correlated with the first function where the coefficient of correlation between the predictor, Profession Test, and function 1 is 0.829, and the coefficient of correlation between GPA and function 1 is 0.540. Whereas the independent variables Friendliness and Profession Test are more correlated with the second function where the coefficient of correlation between the predictor, Friendliness, and function 2 is 0.909, and the coefficient of correlation between the predictor, Profession Test, and function 2 is 0.423 (See: Table 9).
4. We have two discriminant functions as the dependent variable has three categories. The numerical results show that function 1 is more important than function two because 76.5% of the variance among the three groups can be explained by function one whereas only 23.5 % of this variance can be explained by function 2. Also, the degree of relationship between the predictors and groups (canonical correlation) due to function 1 (.533) is more than that due to function 2 (0.329) (See: Table 6).
References
- Burns, R.P., & Burns, R. (2008). Business research methods and statistics using SPSS. Sage.
- Chen, C.J., & Hung, S.W. (2010). To give or to receive? Factors influencing members’ knowledge sharing and community promotion in professional virtual communities. Information & Management, 47(4), 226-236.
- Cramer, C. (2003). Does inequality cause conflict?. Journal of International Development: The Journal of the Development Studies Association, 15(4), 397-412.
- Fernandez, G.C. (2002). Discriminant analysis, a powerful classification technique in data mining. Proceedings of the SAS users international conference, 247-256.
- Fisher, R.A. (1936). The use of multiple measurements in taxonomic problems. Annals of eugenics, 7(2), 179-188.
- Gnanadesikan, R. (2011). Methods for statistical data analysis of multivariate observations. John Wiley & Sons.
- Hair, J.F., Black, W.C., Babin, B.J., Anderson, R.E., & Tatham, R.L. (2010). Multivariate data analysis: A global perspective.
- Hand, D.J. (1981). Discrimination and classification. Wiley Series in Probability and Mathematical Statistics, Chichester: Wiley, 1981.
- Hand, D.J. (1982). Kernel Discriminant Analysis. John wiley & sons, inc., one wiley dr., somerset, N. J. 08873, 1982, 264.
- Inc, S.I. (2016). SAS/STAT. 14.2 User's Guide. Cary, NC: SAS Institute Inc.
- Klecka, W.R., Iversen, G.R., & Klecka, W.R. (1980). Discriminant analysis. Sage.
- Lohnes, P.R. (1971). Multivariate data analysis. J. Wiley.
- McLachlan, G. (2004). Discriminant analysis and statistical pattern recognition. John Wiley & Sons.
- Ramayah, T. (1970). Classifying users and non-users of internet banking in Northern Malaysia. The Journal of Internet Banking and Commerce, 11(2), 1-13.
- Ramayah, T., Jantan, M., & Chandramohan, K. (2004). Retrenchment strategy in human resource management: the case of voluntary separation scheme (VSS). Asian Academy of Management Journal, 9(2), 35-62.
- Silverman, B.W. (1986). Density estimation for statistics and data analysis, Chap and Hall.
- Stevens, J.P. (2012). Applied multivariate statistics for the social sciences. Routledge.