Keywords

ANN, Artificial Intelligence, Machine Learning, Derivatives, Option Greeks.

Introduction

Artificial neural networks have been widely employed in a variety of business applications during the last two & half decades. In the recent years it has gained prominence as we seen significant growth in computational power and storage capacity of modern computers. While financial data is abundant, the inherent nature of financial data creates ambiguity, inconsistency, and it further complicates the use of typical statistical approaches for financial data analysis Brooks et al. (2019). Business and Financial Data are required better analysis and interpretation and in due to the higher dimensionality of the data, its interpretation becomes more challenging. The neural networks are being used by a lot of businesses to solve problems in a lot of different fields and the economic sector, which are usually the job of operations research Boyacioglu et al. (2009). In addition to being useful in science and engineering, artificial intelligence can be used in many different fields, such as social science and the arts Haykin (2004). This makes it unique. For example, in recent years, artificial intelligence (AI) has been used a lot to solve optimization problems in a wide range of fields, including industrial production and petroleum exploration Rahmanifard & Plaksina (2019) and business Araque et al. (2017).

A significant advantage of using ANNs is that they may be used to create models that are easier to use and more accurate from complicated natural systems with massive inputs Jahanvi, (2017). The ANN is discovered to be a highly unique and valuable model for problem solving and machine learning applications. ANN is a model of information management that is comparable to how the organic nervous system of the human brain functions. Globally, interest in brain function has risen dramatically in recent years Wang et al. (2017). According to Haykin (2009a) an ANN is a machine that is akin to the way the human brain does a specific task. For instance, "the human brain is enormous and extremely efficient." The human brain is analogous to an information-processing computer since it "possesses a number of complicated signal computing processes" Haykin, (2009b), which may be readily coordinated to execute a job. The primary component of this brain is its one-of-a-kind architecture for information processing. It is composed of several complexes of interconnected "neurons" in the form of components that collaborate on a daily basis to address specific challenges. The human brain is a typical example of a neural network in operation, since it is connected to transmit and receive signals for human activity.

Artificial Neural Network

Artificial neural network (ANN), also known as Neural Network (NN), is a type of algorithm that was developed with the purpose of creating machines that can replicate the human brain. A neural network is a collection of artificial neurons that are connected in some way. ANNs are artificial adaptive systems that are inspired by the way the human brain functions (McCulloch & Pitts, 1943). They are bodily cellular systems that are capable of acquiring, storing, and utilizing experiential knowledge. As with the human brain, the ANN derives its knowledge from the instances it encounters. The learning process in the human brain system entails changes to the synaptic connections between neurons. ANNs, likewise, modify their structure in response to the output and input data that flow through the network throughout the learning period. There are two parts to data processing in a conventional neural network: learning and applying. Networks must first be trained with either a training database or historical prices. A known value is in this dataset. There is an input vector and an output vector with the same value. Every single input and output is a node or neuron in its own right, and they all connect to each other. In addition, one or more layers are hidden. The goal of the learning phase is to adjust the weights of connections between different layers or nodes. Next, the learning samples will be set up. An iterative method will be used to feed a sample into the network and compare its outputs to the known outputs. As soon as it isn't equal, weights of connections will be changed to make the difference between them as small as possible. After the learning phase, the network is checked against the validation datasets to make sure it works.

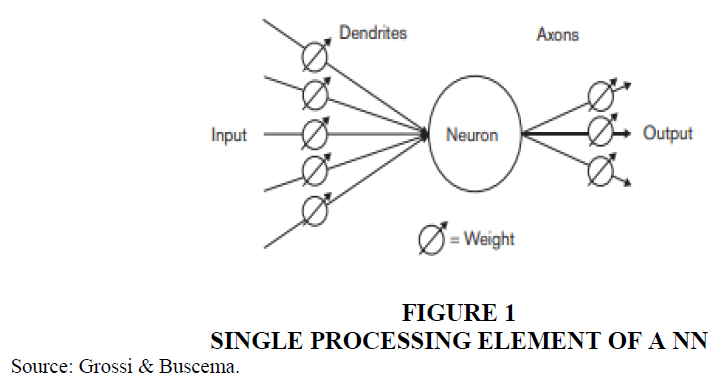
The ANN's fundamental elements are nodes, also known as processing elements (PE), and connections. Each node has its own input, which it uses to receive messages from other nodes and/or the environment, and an output, which it uses to interact with other nodes and/or the environment. Finally, each node has a function f that converts its global input to output (Figure 1). Each link is defined by the strength with which it excites or inhibits pairs of nodes.

Positive values correspond to excitatory connections, whilst negative values correspond to inhibitory connections McClelland & Rumelhart (1986). The relationships between the nodes are dynamic and can change over time. This dynamic initiate the learning process across the ANN Marr (1975). The 'Law of Learning' refers to the process through which nodes adapt themselves. The overall dynamic of an ANN is time dependent. Indeed, in order for the ANN to adjust its own connections, the environment must operate on it several times (Rosenblatt,1958). The environment in which the ANN operates is comprised of data. Thus, learning is a critical mechanism that characterizes ANNs, which are referred to as adaptive processing systems. The learning process is one method for adapting an ANN's connections to the data structures that comprise the environment, and hence for 'understanding' the environment and the relationships that define it (Personnaz, 1986). A recent review paper Grossi & Buscema, provides a great introduction to the basic concept of ANN (Artificial Neural Network).

Typical Usage on ANN

The most common problem that an ANN can solve is as follows: given N variables for which data collection is straightforward, and M variables that are dissimilar to the first and for which data collection is difficult and costly, determine whether it is possible to predict the values of the M variables using the N variables. When the M variables occur after the N variables, the problem is referred to as a prediction problem; when the M variables are dependent on some form of static or dynamic component; the problem is referred to as one of recognition, discrimination, and/or extraction of essential qualities. To apply an ANN appropriately to this sort of situation, we must first conduct a validation process. We must begin with a sufficiently large sample of cases in which both the N variables (known) and the M variables (to be found) are known and dependable.

ANN in Finance

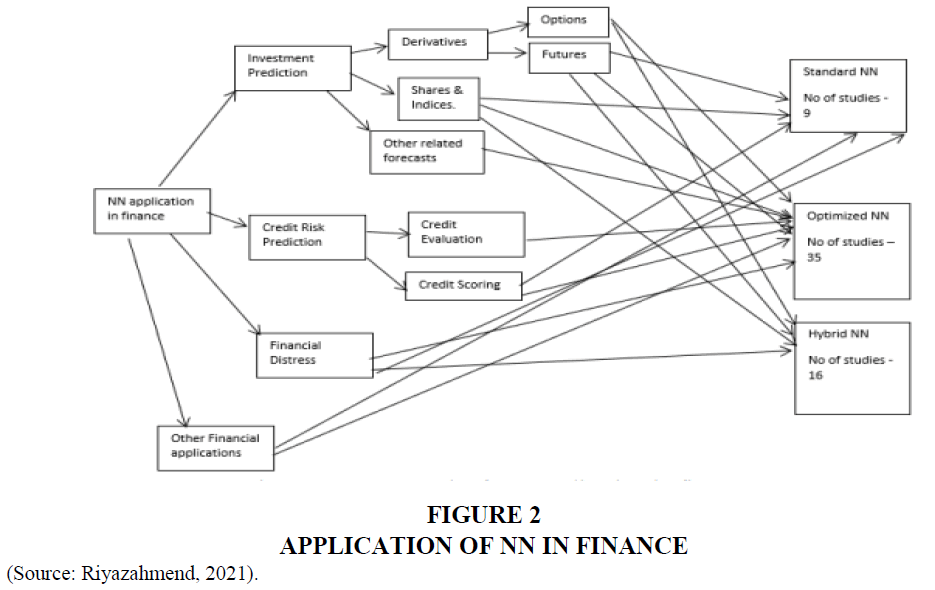
In one of the comprehensive reviews Riyazahmend (2021), defines and investigates the use of neural networks in finance via the lens of four key categories: investment prediction, credit evaluation, financial hardship, and other financial applications. This has been depicted in Figure 2. Similarly, the review divides the neural network approaches utilized in each category into conventional, optimized, and hybrid neural networks. Additionally, the accuracy measurements utilized in the study work vary greatly, which complicates comparing a NN under each category and limits the scope of formalizing a theory to choose the optimal network model under each category. There are other noticeable review work in the application of NN in Finance Feldman & Kingdon (1995); Wong & Selvi (1998); Vellido et al. (1999); Krishnaswamy et al. (2000); Coakley & Brown (2000); Fadlalla & Lin (2001); Huang et al. (2007); Cavalcante et al. (2016); Huang et al. (2020) which shed light in the way NN is being applied.

Another review article Burrell & Folarin (1997) presents a compilation of current research topics on neural networks in the financial realm from a variety of sources. It analyzes a variety of neural network systems for financial applications, ranging from early prototypes to fielded products. It analyzes the neural network systems' success rate and their performance in handling certain financial challenges.

Review of Neural Network (NN) in Derivative Pricing, Hedging and Risk Management

Financial derivatives are financial products that are connected to a specific financial instrument, indicator, or commodity and that allow for the trading of certain financial risks in their own right on financial markets. Financial derivatives transactions should be regarded separately from the underlying transactions to which they may be tied. A financial derivative's value is determined by the price of an underlying asset or index IMF (2018). Complexity of the Pricing of a Derivative contract depends on the structure of the derivatives. While Vanilla Equity Options can be priced using Simple Black-Scholes Model Macbeth & Merville (1979) but an exotic derivative structure require more complex multi-factor stochastic volatility models Taylor (1994). A related research paper Smith (1976) has provided a comprehensive account of initial work of Derivative pricing. This article reviews: (1) Black and Scholes' development of the general equilibrium option pricing model, as well as subsequent modifications by Merton and others; (2) empirical validation of these models; and (3) applications of these models to the valuation of other contingent claim assets, such as leveraged firm debt and equity, as well as dual purpose mutual funds.

Shortcomings of the conventional option pricing model

Black-Scholes model makes distribution assumptions. The Black-Scholes option-valuation equilibrium model generates option pricing on the premise that prices follow a continuous time path and that instantaneous volatility is not stochastic which is not a good assumption as this has been proved wrong in various published research Taylor (1994). The neural network, which employs the same financial data as the Black-Scholes model, makes no distribution assumptions and instead learns from past data the correlations between the financial input data and the option price Malliaris & Salchenberger (1993). Table 1 depicts a comparative analysis of Black-Scholes pricing model to that of Neural Network based models.

Table 1 Summary of Comparison Analysis of Black-Scholes vs. Neural Network based options pricing
Reference	Short Comings of Black- Sholes	Neural Network based Solution	Neural Network Benefits
Amilon (2003)	Impractical Assumptions	Relaxed Assumptions	More applicability
Bennell & Sutcliffe (2004)	Inaccurate Pricing of deep in/out of the money with longer expiry	Better pricing of deep in/out of the money options	More applicability and versatility
Grohs et al. (2018)	Issues with dimensionality in Numerical Approximations.	Easily approximate High dimensional functions.	Ability to handle complex scenarios.
Malliaris & Salchenberger	Fail to replicate volatility quotes on edges of the volatility wings	Deep In/out of the money options can replicate implied volatility at the wings	More Consistent Pricing
Chen et al. (2021)	Difficult to analytical solutions always.	Possible to use a functional form on the basis of neural network e.g., Laguerre Polynomial as a basis function of neural network.	Analytical solution possible which minimizes computational overheads by not using any kind of simulation.
Zapart (2003)	Flat forward Volatility assumptions	Forward Volatility evalove through a deep learning Process	Better Pricing and Hedging.
Lin & Yeh (2013)	Not satisfactory pricing during high volatility region.	NN uses back propagation neural network to pricing options in higher volatility regions.	Better pricing and replication of options.

Summary of the Review

Hutchinson-Lo-Poggio showed that it is indeed possible to use a Neural Network to price S&P futures options.

In one of the Carverhill et al. (2003) it was investigated that optimal method for setting up and training a Neural Network for option pricing and hedging. Additionally, they concluded that a Neural Network can provide more accurate hedging parameters than the typical option pricing model. They analyze S&P futures options data from 1990 to 2000.

Some of the early application of Neural network in pricing and hedging of Derivative (Garcia & Gencay, 2000) used a feed forward neural network model. They use a feed forward neural network model to estimate a generalized option pricing formula with a functional structure comparable to that of the standard Black–Scholes formula. When the option pricing function is homogeneous of degree one with regard to both the underlying asset price (St) and the strike price, this functional structure is achieved (K). They demonstrated how this generalized Black–Scholes shape may be used to improve price accuracy. Rather of creating a neural network that maps the ratio St/K and the time to maturity () directly to the derivative price, we split the pricing function into two pieces, one controlled by the ratio St/K and the other by a time to maturity function. The results suggest that when compared to a feedforward neural network with no hint, the homogeneity hint always minimizes the out-of-sample mean squared prediction error. Both feed forward network models, with and without the hint, provide identical delta-hedging errors that are minor in comparison to the Black–Scholes model's hedging performance. The model with hint, on the other hand, delivers a more reliable hedging performance.

In a separate piece of work, researchers Anderes et al. (1998) uses statistical inference techniques to develop neural network models capable of explaining the values of call options on the German stock index DAX. By examining the explanatory power of numerous variables used as network inputs, they get insight into the option market's pricing mechanism. The results demonstrate that statistical specification procedures result in sparse networks that perform better out-of-sample than the Black/Scholes model.

In another related work Morelli et al. (2004) the topic of option pricing is addressed using neural network algorithms, which are used to replicate the nonlinear behavior of such financial derivatives. Two distinct types of neural networks are contrasted in depth, namely multi-layer perceptrons and radial basis functions. The study is conducted for both ordinary European and American options, and includes an evaluation of the Greek letters, which are required for hedging reasons. A detailed numerical examination demonstrates that, following a thorough training phase, neural networks are capable of accurately predicting the value of choices and Greek letters while maintaining a competitive computing time.

In one of the types of research Montagna et al. (2003), summarizes the advancements in the development of efficient computer methods for pricing financial derivative and solving complex path integrals using neural network. A first method is based on a route integral approach to option pricing, whereas a second algorithm employs a neural network parameterization approach to option pricing. The correctness of the two methodologies is confirmed by comparisons to the findings of traditional quantitative finance processes.

In similar research Gencay & Qi (2001) They look at the effectiveness of cross validation, Bayesian regularization, early stopping, and bagging for pricing and hedging derivatives with daily S&P 500 index daily call options from January 1988 to December 1993. Some of their results show that Bayesian regularization can make a big difference in how well the Black-Scholes and neural-network (NN) models do at pricing and delta-hedging for a few years. While early stopping doesn't change the pricing errors, it significantly reduces the hedging error (HE) in four of the six years we looked at, which is a lot. Bagging, even though it is the most computationally intensive, seems to be the best way to price and hedge deltas. So the standard deviations for bagging are far less than for the baseline model in all six years. The standard deviation of the average HE is far less than for the baseline model in at least five out of six years, too.

Research Amilon (2003) was done to determine if a neural network (MLP) can be used to find a call option pricing formula that is more closely related to market prices and the underlying asset's attributes than the Black–Scholes formula. From 1997 to 1999, the neural network approach is used to determine the out-of-sample pricing and delta hedging of daily Swedish stock index call options. The need of hedging analysis is emphasized further in this article. The Black–Scholes model with historical and implied volatility estimates is used as a benchmark. Comparisons demonstrated that neural network models beat benchmarks in terms of pricing and hedging. The statistical significance of the data is determined using a moving block bootstrap. While neural networks are better, their findings are occasionally inconsequential at the 5% level.

Another research Plooy & Venterm (2021) compares the pricing performance of two learning networks, an artificial neural network and a bootstrap aggregating ensemble network, for pricing the Johannesburg Stock Exchange (JSE) Top 40 European call options using a created implied volatility surface. Additionally, in a separate numerical experiment, the numerical accuracy of the higher performing network was compared to that of a Monte Carlo simulation. When pricing derivatives in a multi-curve framework, it was discovered that the bootstrap aggregating ensemble network outperformed the artificial neural network and gave price predictions within the error boundaries of a Monte Carlo simulation.

Palmer (2019) tried to optimize the computational resources in derivative pricing problem. To do this, a unique hybrid evolutionary algorithm (EA) based on particle swarm optimization (PSO) and differential evolution (DE) is proposed and used to the challenge of calibrating the Heston stochastic volatility model, along with many additional state-of-the-art variations of PSO and DE. It is discovered that state-of-the-art DEs perform exceptionally well in terms of calibration, and that earlier usage of rudimentary DEs in the literature underestimated their utility. Following that, the usage of neural networks in conjunction with EAs is examined for approximating the answer to derivatives pricing models. To approximate the closed form solution for European, Asian, and American style choices, a collection of neural networks is trained using Monte Carlo (MC) simulation data. The findings are equivalent to those obtained using Markov chains, but the offline evaluation of the price through neural networks is orders of magnitude quicker and more computationally efficient. Finally, the usage of customized hardware for numerical derivatives pricing is discussed. The solver given here implements a data-flow model for pricing derivatives in an energy-efficient manner, with the potential to be integrated into larger high-speed/low-energy trading systems.

One of the works Liu et al. (2019) presents a data-driven methodology for valuing financial options and calculating implied volatilities using an Artificial Neural Network (ANN) in order to accelerate the associated numerical approaches. Due to the fact that ANNs are universal function approximators, this technique efficiently trains an optimized ANN on a data set generated by a complex financial model and then executes the trained ANN as an agent of the original solver. This methodology is evaluated using three alternative solvers: the analytic solution for the Black-Scholes equation, the COS method for the Heston stochastic volatility model, and Brent's iterative root-finding method for calculating implied volatilities. The numerical results demonstrate that the ANN solver may greatly cut computing time.

One of the papers Bennel & Sutcliffe (2005) compares Black Scholes to an artificial neural network (ANN) for pricing European-style call options on the FTSE 100 index. This is the first comprehensive examination of ANNs' performance in pricing UK options, and the first to incorporate dividends into the closed-form model. The ANN definitely outperforms Black–Scholes for out-of-the-money options. If the sample space for in-the-money options is narrowed to exclude deep in-the-money and long maturity options (3.4 percent of total volume), the ANN performs similarly to Black–Scholes. The ANN's superiority is surprising, given that Black–Scholes is best known for pricing European-style equity options. It suggests that ANNs may have a significant role to play in pricing other options for which there is either no closed-form model or the closed-form model is less successful than Black–Scholes for equity options.

Horvath et al. (2020) describe a neural network-based calibration technique that completes the calibration job for the whole implied volatility surface in a few moments. The methodology is applicable to a wide variety of volatility models, including second-generation stochastic volatility models and the rough volatility family, as well as to a wide variety of derivative contracts. In this study, neural networks are utilized to approximate complicated pricing functions that are difficult to express or time-consuming to analyze using existing methods. The manner in which accessible data is taken and utilized has an effect on network performance: Calibration is accomplished using a grid-based technique inspired by the representation of implied volatility and option prices as a collection of pixels. We demonstrate how this approach expands the possibilities for quantitative modeling. The calibration bottleneck imposed by delayed derivatives pricing is removed, and stochastic volatility models (classical and rough) may be treated with considerable flexibility, as the framework also allows for the input of the forward variance curve. We illustrate the calibration performance on both simulated and historical data, on a variety of derivative contracts, and on a variety of example models of increasing complexity, as well as highlighting some of the potential benefits of this method to model recognition.

In an interesting Yao et al. (2000) research back propagation neural networks are used to anticipate the option prices of Nikkei 225 index futures in this study. Different groupings of data have different results in terms of accuracy. The results indicate that a neural network option pricing model beats the standard Black–Scholes model in turbulent markets. The Black Scholes model, on the other hand, is still useful for pricing at-the-money options. When utilizing a neural network model, data should be partitioned according to its moneyless. Those who want lower risk and higher returns can use the findings of the standard Black–Scholes model, while those who prefer higher risk and higher returns can utilize the results of the neural network model.

Hirsa et al. (2019) use supervised deep neural networks (DNNs) to price and calibrate vanilla and exotic options with and without stochastic volatility. They train our neural network models with a variety of different layer counts, neurons per layer counts, and activation functions to see which combinations perform best experimentally. They examine a variety of alternative loss functions and optimization procedures for training. They demonstrate that deep neural networks accelerate option pricing tenfold when compared to frequently used option pricing methods, which results in super-fast calibration and parameter estimation.

Expanding the variations, one research Samur & Temur (2009) takes into account not just European call options, but also American call and put options, as well as European put options. Three distinct data sets are utilized to train three distinct ANN models. One contains only variables that are immediately observable in the economic environment, such as the strike price, the spot price, the interest rate, the contract's maturity, and the contract's kind. Others incorporate an additional input that is not observable data but rather a parameter, such as volatility. With this detailed data, the performance of ANN is studied in terms of put/call ratios, American/European ratios, and moneyness ratios, as well as whether the introduction of volatility to neural network analysis improves prediction performance or not. The study's most remarkable finding is that ANN performs better when pricing call options than put options, and that using the volatility parameter as an input does not increase performance.

Barunikova & Barunik (2011) examined artificial neural networks' ability to price European-style call and put options on the S&P 500 index using daily data from June 2004 to June 2007. They categorize the data set according to its monetary value and maturity date. They then assign a price to each choice within each category. The results demonstrate that neural networks beat the benchmark ad hoc Black-Scholes model in all categories of call and put options, with much smaller pricing mistakes. Additionally, the discrepancies between ad hoc Black-Scholes and neural network mistakes get larger when moneyness or time to maturity increases. They demonstrate that neural networks can adjust for the Black-Scholes maturity and moneyness biases even in the absence of a volatility input.

One of the researches Pagnottoni (2001) explains that following the rapid surge in interest in Bitcoins and cryptocurrencies in general financial products, as well as associated research, are still fairly immature. As such, this essay will attempt to develop a reasonable pricing model for options on this unique basis. This is accomplished using an artificial neural network methodology, with input layers consisting of conventional pricing models such as the trinomial tree, Monte Carlo simulation, and explicit finite difference method. The results indicate that when using traditional approaches, options written on Bitcoin are consistently overvalued, but the suggested neural network model achieves a significant improvement in price prediction.

A similar research article Gradojevic et al. (2009) examines the pricing of S&P-500 European call options using a nonparametric modular neural network (MNN) model. The modules are organized according to the time to maturity and liquidity of the options. Interest is a degree one homogeneous function of the option price function with regard to both the underlying index price and the strike price. In comparison to a variety of parametric and nonparametric models, the MNN technique regularly outperforms others in terms of out-of-sample pricing. We argue that the modularity of traditional feed forward neural network option pricing models enhances their generalizability.

In an analysis Germain et al. (2021), they introduce machine learning approaches and deep reinforcement learning-based algorithms for solving nonlinear partial differential equations and dynamic optimization problems that arise in financial engineering when making investment decisions and pricing derivatives. We review recent publications, highlight recent improvements, notably in the completely nonlinear condition, and compare alternative techniques employing numerical testing on a number of financial applications. We end by highlighting some additional research areas.

One of the studies Ratku & Nuemann (2022) shows how a deep feed-forward neural network that has been trained to price derivatives can also is used to calculate these sensitivities. As an alternative to automated differentiation, the suggested method does all of a multilayer feed-forward neural network's first and second order derivatives at the same time. It does this by taking into account the input characteristics of the network. The study estimates how well the new method will work over a previous, public version of automated differentiation. It looks at how well the new method does over a wide range of network sizes. These networks have the same number of input parameters as a lot of popular financial models that have a lot of different types of volatility. A case study shows that the proposed sensitivity calculations are correct in terms of numbers by calculating the price sensitivities of European options with stochastic volatility. Financial applications aren't the only thing this article talks about, but the results are the same for all deep feed-forward neural networks with smooth activation functions.

A data-driven technique termed CaNN (Calibration Neural Network) is presented in one of the studies Liu et al. (2019) for calibrating financial asset price models using an Artificial Neural Network (ANN). Optimal model parameter values are determined by training hidden neurons within a machine learning framework using accessible financial option prices. The framework is divided into two sections: a forward pass in which they train the ANN's weights offline, valuing options under a variety of different asset model parameter settings; and a backward pass in which we evaluate the trained ANN-solver online, with the goal of determining the weights of the neurons in the input layer. Rapid on-line learning of implied volatility using ANNs in conjunction with an adapted parallel global optimization method alleviates the computation bottleneck and provides a fast and reliable technique for calibrating model parameters while avoiding getting stuck in local minima as much as possible. Numerical studies demonstrate that this machine-learning approach can be used to efficiently and accurately calibrate the parameters of high-dimensional stochastic volatility models.

One published paper De Gennaro Aquino & Bernard (2020) used neural networks to compute constraints on the pricing of multi-asset derivatives given information on the values of linked payoffs. We focus on European basket options as a primary example, but also include data on the pricing of other comparable options, such as spread options and/or basket options on subindices. We demonstrate that, in most situations, introducing additional restrictions results in significantly narrower limits.

One of the Neural Network applications in Derivatives Dimitroff et al. (2018) replicated the calibration of the Heston model to equities volatility surfaces using a supervised deep convolutional neural network. They accomplish this by treating the implied volatility surface, along with some auxiliary data, such as the strikes and moneyness of the corresponding options and equity forwards, as a three-dimensional input tensor for the neural network, analogous to a color channel image representation such as RGB. We use inception layers with (1;1), (1;3), and (2;1) dimensional kernels to extract the key characteristics from the input data. The exact option is justified by the call pricing surface's no-arbitrage criteria. In terms of modeling a local surface, the (1;3) filters with varying weights can model position, slope, and curvature in the moneyness direction, and the (2;1) filters may model position and slope in the maturity direction. The neural network was developed using the free and open-source tensor-flow framework.

As a continuation, one of the published works Montesdeoca & Niranjan (2016) extended the previous study Hutchinson by examining the model with new inputs relevant to option pricing and demonstrating that the approximation accuracy may actually be improved. Additional elements include volume traded, historical volatility, observed interest rates, and combinations of these. Along with actual evidence demonstrating how these factors aid in predicting option prices, we investigate the prediction errors of several models using volatility and volume traded as inputs and discovers an intriguing link between their contributions.

One of the research articles Alexandre Carbonneau & Godin (202) proposes a generic and tractable technique based on deep reinforcement learning for implementing the equal risk pricing framework for financial derivatives pricing under extremely general settings. The equal risk pricing methodology comprises determining a derivative price that equates the ideally hedged residual risk exposure associated with the long and short contingent claim positions, respectively.

Recent study Itkin (2019) demonstrates how advancements in the fields of artificial intelligence, machine learning, and the computer industry have resulted in a continuous boom in the application of these approaches to complicated problems in both science and industry. Naturally, the financial business and mathematical finance are analogous. We address a traditional mathematical finance topic - calibrating option pricing models to market data - since it has lately garnered considerable interest from the financial community in the context of deep learning and artificial neural networks. We discuss some of the shortcomings of existing techniques and provide fixes that increase both calibration performance and accuracy. Additionally, we address a previously unresolved issue of no-arbitrage pricing when employing a trained neural network Anderson & Ulrych (2022).

A related piece of work Ferguson & Green (2016) use deep learning to determine the value of derivatives. The strategy is generally applicable, and we illustrate it with a call option on a basket of equities. We demonstrate that the deep learning model is very accurate and extremely quick, capable of providing values a million times faster than conventional algorithms. We design a mechanism for randomly generating adequate training data and investigate the effect of numerous factors on model speed and accuracy, including layer breadth and depth, training data quality and quantity.

As mentioned in the study article Lajbcygier (2004), several investigations across a variety of financial markets over the last decade have demonstrated the inaccuracy of standard option pricing models. Numerous researchers have resorted to artificial neural networks to increase their accuracy (ANNs). In this study, a neural network is limited in such a way that pricing at option-price borders must be logical. Constraints alter the ANN's regression surface, improving the accuracy of option pricing in the vicinity of the borders. These limits result in statistically and economically substantial outperformance when compared to the most accurate conventional and non-traditional option pricing models.

In an early published paper Dugas et al. (2000), it was demonstrated that adding previous information about a specific task into the architecture of a learning algorithm may significantly boost generalization performance. We consider a scenario in which we are aware that the function to be learnt is non-decreasing in two of its parameters and convex in one. To do this, we propose a class of functions comparable to multi-layer neural networks but that (1) possess those features and (2) act as a universal approximator of continuous functions possessing these and other properties. They use this novel class of functions to the modeling of call option prices.

A group of academics Yang et al. (2017) have suggested a neural network technique for pricing European call options that outperforms certain existing pricing models and provides guarantees that its forecasts are economically fair. To do this, we develop a type of gated neural networks capable of autonomously learning to divide and conquer the problem space in order to provide robust and accurate pricing. We next develop instantiations of these networks that are 'rational by design' in the sense that they naturally encode a valid call option surface that adheres to no arbitrage criteria. This combination of human perspective with data-driven learning results in much improved generalization in pricing performance, ensures the model's predictions are sane, and produces econometrically relevant byproducts such as risk neutral density.

A simple and successful nonparametric technique for predicting option prices is provided in one of the papers Liang et al. (2009). It is based on neural networks (NNs) and support vector regressions (SVRs). We began by modifying the enhanced conventional option pricing algorithms to enable forecasting of option prices. Second, we used NNs and SVRs to further reduce the parametric approaches' predicting mistakes. Because conventional approaches mirror the patterns in the movement of actual option prices, adopting them in the first stage enables NNs and SVRs to focus their resources on nonlinear curve approximation in the second stage, significantly reducing forecasting mistakes. Finally, thorough experimental experiments using data from the Hong Kong option market proved that NNs and SVRs are capable of increasing forecast accuracy.

Volatility modeling is a critical component of option pricing, and the use of neural networks to simulate volatility has been tried. In one such study Karali, the authors employed OEX (a 1986 index developed by the Chicago Board Options Exchange). This volatility index is calculated using the implied volatility of eight distinct OEX options and is intended to be a trustworthy approximation of the market's consensus expectation for short-term volatility. Additionally, it establishes a benchmark for volatility derivatives. They provide a comparable metric for the market's short-term projection of Deutschemark volatility in this study. They examine the index's time series features, investigate a closed-form solution for pricing derivative instruments based on the index, and price options based on the index using neural network approaches. Finally, they look at a practical example of how to use index futures to mitigate the volatility risk associated with a portfolio of Deutschemark options. Neural network technology was used in two distinct areas for this project. The volatility index was forecasted using a single neural network. A second neural network was utilized to determine the values of the options exchanged on this contract. Commercial neural network-based systems have been proven to outperform systems based on classical approaches in time series and digital signal processing applications.

The availability of continuous-time diffusion models that match the market prices of a given collection of options is a key question in quantitative finance. Traditionally, models with precise or approximate fits have been discovered by a combination of intuitive, theoretical, and empirical investigation. One of the significant contributions of this research Vadori (2022) is to demonstrate how an appropriate game theoretical formulation of this problem might aid in resolving this dilemma by utilizing recent advances in deep multi-agent reinforcement learning to search in the space of stochastic processes. More significantly, we expect that our methodologies may be used and developed by the community to address critical issues in that field, such as the combined SPX-VIX calibration challenge. Our studies demonstrate that we can learn both local volatility and the path-dependence necessary for the volatility process to reduce the price of a Bermudan option.

The study conducted by Zhang et al. (2022) proposes a hybrid strategy based on deep neural networks for forecasting short-term power prices. To be more precise, the suggested technique employs the categorical boosting (Catboost) algorithm for feature selection and a bidirectional long short-term memory neural network (BDLSTM) for forecasting. To assess the suggested approach's performance, hourly power pricing data from the Nord Pool market from 2018 are used as a case study. Additionally, the suggested approach's performance is compared to that of a multi-layer perception (MLP) neural network, support vector regression (SVR), ensemble tree, ARIMA, and two contemporary deep learning-based models, gated recurrent units (GRU) and LSTM models. This study validates the suggested technique using a real-world dataset from the Nord Pool market. Model performance is quantified using mean percentage error (MAPE), root mean square error (RMSE), and mean absolute error (MAE). Experiments demonstrate that the suggested model yields fewer predicting errors than the other models evaluated in this study, despite the fact that training and forecasting are more time intensive.

In one study Gaspar et al. (2020), Neural Networks (NNs) were employed to price American put options. We present two different NN models—one basic and one more complex and compare their performance using the Least-Squares Monte Carlo (LSM) approach. This analysis makes use of American put option market pricing for four significant US companies: Procter & Gamble Company (PG), Coca-Cola Company (KO), General Motors (GM), and Bank of America Corp. (BAC). Their dataset includes all options exchanged between December 2018 and March 2019. Although NN models outperform LSM on average, the simpler model (NN Model 1) outperforms LSM pretty closely. Additionally, the second NN model surpasses the other models significantly, with an RMSE about 40% lower than the one reported by LSM. The decreased root mean square error is constant across industries, striking levels, and maturities. In summary, all approaches exhibit a high degree of accuracy; but, following calibration, NNs outperform all other methods in terms of execution time and Root Mean Squared Error (RMSE).

Financial models with stochastic volatility or jumps are significant as alternative option pricing models to the conventional Black Scholes model because they are capable of fitting a variety of market volatility patterns. Recently, academics have focused their attention on machine learning models due to their enhanced forecast accuracy when pricing financial derivatives.

One of the studies Huisu Jang & Jaewook Lee (2019) proposes a generative Bayesian learning model with a prior representing a risk-neutral pricing structure for deep ITM and deep OTM options that are seldom traded. We undertake a thorough empirical research comparing classical financial option models to machine learning models in terms of model estimate and prediction, utilizing S&P 100 American put options from 2003 to 2012. The results reveal that machine learning models outperform traditional financial option models in terms of prediction performance. We notice, in particular, that the generative Bayesian neural network model performs the best in terms of total prediction performance.

One of the studies Chen & Wan proposes a framework for estimating the prices and deltas of American options in high dimensions using deep neural networks. The framework is composed on a series of neural networks, each of which learns the difference between neighboring timesteps' pricing functions. We define the loss function as the least squares residual of the corresponding backward stochastic differential equation. Our proposed methodology generates prices and deltas throughout the entire spacetime, not only for a particular point (e.g. t =0). The computing cost of the suggested technique is quadratic in dimension, which circumvents the curse of dimensionality that exists with state-of-the-art approaches. Our numerical simulations validate these contributions and indicate that the proposed neural network architecture outperforms existing techniques in high dimensions.

Option Greeks and Option sensitivity calculation is a critical aspect of option hedging. One of the research paper Tsaih (1999) determine if sensitivity analysis can be used not only to read the information inherent in artificial neural networks (ANNs), but also to evaluate the success of ANN learning. This item is simulated using the Black-Scholes formula. The Black-Scholes formula, in which the mapping between the call price and five important variables is theoretically closed, is appropriate for validating the sensitivity analysis approach used to read ANN knowledge. To establish the validity of assessing the efficacy of ANN learning, two distinct ANNs are constructed and their sensitivity analyses on learning patterns are compared. Both the sensitivity analysis of ANNs and the partial derivative of the Black-Scholes formula are compatible with the experimental results. Additionally, they demonstrate that sensitivity analysis may be used to assess the success of ANN learning.

Gierjatowicz et al. (2020) used neural networks and classical stochastic differential equations (SDEs) to derive resilient constraints for derivatives pricing and appropriate hedging strategies while incorporating relevant market data. The resultant model, dubbed neural SDE, is an instantiation of generative models and is strongly related to causal optimum transport theory. Consistent calibration of neural SDEs under risk-neutral and real-world conditions is enabled by neural SDEs. As a result, the model may be used to generate market scenarios for the purpose of evaluating risk profiles and hedging strategies. They create and analyze unique algorithms that are required for the efficient usage of neural SDEs. Our technique is validated numerically using both local and stochastic volatility models.

The relevant article Schittenkopf & Dorffner (2001) describes a novel semi-parametric technique for extracting risk-neutral density from option prices that is based on an expansion of the notion of mixed density networks. The essential concept is to represent the form of the risk-neutral density as a function of the time horizon in a flexible, nonlinear fashion. This captures stylized facts such as negative skewness and excessive kurtosis. The technique is shown using a massive dataset of intraday options data on the FTSE 100 from LIFFE. It is demonstrated that it outperforms both the basic and extended Black-Scholes models in terms of out-of-sample pricing accuracy. Additionally, it outperforms a more complex GARCH option pricing model that incorporates a time-dependent volatility mechanism. From a risk management standpoint, the extracted risk-neutral densities give significant information for estimating value-at-risk.

The typical technique for pricing financial options is the Black–Scholes (BS) model. Although theoretically sound, the model's option prices frequently deviate from those observed in financial markets. A similar article 72. Sunisa Amornwattana et al. (2007) used a hybrid neural network to preprocess financial input data in order to improve option market price estimates. This model is divided into two halves. The first section involves the development of a neural network for the purpose of estimating volatility. The second element is a neural network that was designed to evaluate the difference between the findings of the BS model and actual market option pricing. The option price that results is thus a summation of the BS model and the network response. The hybrid system with a neural network for predicting volatility outperforms either the BS model with historical volatility (HV) or the BS model with volatility estimated by the neural network in terms of pricing accuracy.

Researchers provide a model-free option pricing strategy using neural networks in a research paper Von Spreckelsen et al. (2014), which may be used for real-time pricing and hedging of FX options. In comparison to well-established theoretical models, a critical benefit of our method is the simultaneous pricing of multiple strike prices and the sparing use of real-time input data. To evaluate its suitability for high-frequency trading, we conduct an empirical run-time trading simulation using a tick dataset of EUR/USD options on four-week currency futures. Through two distinct neural network topologies, theoretical option prices obtained from the Black model compete against nonparametric option pricing in extremely brief non-overlapping 15-minute out-of-sample periods. We demonstrate that learning networks' approximated pricing functions are useful for creating rapid run-time option pricing assessment since their performance is somewhat better than theoretical prices. The network function derivation is also advantageous for implementing hedging strategies. We find that closed-form pricing models' performance is heavily dependent on the volatility estimator, whereas neural networks avoid this estimate issue but require market liquidity to train.

The Black–Scholes formula is a well-known mechanism for pricing and hedging derivatives. However, it is predicated on a slew of extremely problematic assumptions. The purpose of this research Amilon (2003) is to evaluate if a neural network can be utilized to develop a call option pricing formula that is more closely connected to market prices and the underlying asset's characteristics than the Black–Scholes formula. Between 1997 and 1999, we employed a neural network technique to compute the out-of-sample pricing and delta hedging of daily Swedish stock index call options. This paper emphasizes the importance of hedging analysis even more. As a benchmark, the Black–Scholes model with historical and implied volatility estimates is utilized. In terms of pricing and hedging, comparisons show that neural network models outperform benchmarks. A moving block bootstrap is used to determine the statistical significance of the data. While neural networks are superior, several of the findings are non-significant at the 5% level.

In a separate study Dindar & Marwala (2004), the conventional multilayer perceptron (MLP) and radial basis functions (RBF) were employed to simulate the data, and the resulting findings were compared to those obtained using a committee of networks. Particle swarm optimization was then used to optimize the MLP and RBF architectures (PSO). The outcomes of the 'optimal architecture' networks were then compared to those of the standard and committee networks. They discovered that, at the cost of computing time, the 'optimal architecture' RBF and MLP networks outperformed both unoptimized and committee of networks.

Using a feed-forward neural network, Anders et al. (1998) present a unique way for speeding the pricing of American options to near-instantaneity. This neural network is trained on the stochastic volatility specification of choice (e.g., Heston). This methodology enables parameter interpretability, which regulators normally expect, and establishes our method in the field of Explainable Artificial Intelligence (XAI) for finance. They demonstrate that, as compared to conventional Monte Carlo or Partial Differential Equation-based pricing approaches, the proposed deep explainable pricer results in a speed-accuracy trade-off. Additionally, the suggested technique is relevant in a market-making context since it allows for the pricing of derivatives with route dependent and more complicated payoffs and is tractable due to its sufficient precision of calculation and tractable nature.

Another study Boek et al. (1995) offered a novel technique of pricing choices. The strategy is based on the addition of an artificial neural network (ANN) trained on the difference between the standard model and actual options data to a conventional model. The accuracy of the pricing was proved using genuine All Ordinaries Share Price Index (AO SPI) options on futures. This hybrid technique is demonstrated to be more accurate than either the conventional model or the ANN alone.

In comparison to the original BSM (Black-Scholes-Merton) option pricing method, a recently published paper Qian et al. (2022) introduced a genetic algorithm into the option pricing process, based on the characteristics of financial data, and constructed a GA-BP neural network (Neural Networks) option pricing model and conducted an empirical analysis of European call options based on the Shanghai and Shenzhen 300 Index. The research findings indicate that the GA-BP neural network algorithm produces a more accurate option price computation than either the BP neural network model or the standard BSM approach, which is beneficial for forecasting option prices in financial practice to a certain extent.

One of the studies Chen & Sutcliffe (2012) compares the performance of artificial neural networks (ANNs) with the modified Black model in terms of pricing and hedging short sterling options. Standard and hybrid ANNs are trained to create option pricing using high-frequency data. In terms of pricing call and put options, the hybrid ANN outperforms both the modified Black model and the regular ANN substantially. Hedge ratios for short sterling option bets hedged with short sterling futures are calculated using standard and hybrid ANN pricing models, the modified Black model, and also standard and hybrid ANNs trained directly on the hedge ratios. The performance of hedge ratios derived from ANNs trained directly on actual hedge ratios is much better than that of hedge ratios derived from a pricing model or the modified Black model.

A fascinating study Andreou et al. (2008) compares the parametric Black and Scholes, Corrado and Su models, and Artificial Neural Networks' capacity to price European call options on the S&P 500 using daily data from January 1998 to August 2001. They employ a variety of historical and inferred parameter estimates. Apart from regular neural networks, we include hybrid networks in our research since they contain information from parametric models. Our findings are noteworthy and contradict past research. They demonstrate that hybrid artificial neural network models based on Black and Scholes outperform both regular neural networks and parametric ones. Additionally, we examine the economic relevance of the best models through the use of trading techniques (extended with the Chen and Johnson modified hedging approach). We discover that profitable possibilities exist even when transaction fees are present.

Results Analysis and Discussions

Analysis

Summary of review of Nn in derivative pricing, hedging and risk management was explained in Table 2

Table 2 Summary of Review of NN in Derivative Pricing, Hedging and Risk Management
References	Neural Network Model & Methodology	Application	Improvement Aspect	Year
Boek et al. (1995)	Generalized Neural Network basis framework	More Accurate pricing of Options	Accuracy	1995
Karali et al. (1997)	NN As Approximator	Improved Analytical Calculation	Computational Speed	1997
Anderes, Koran & Schmitt (1998)	Statistical Inference technique	Better out of the sample pricing of options	Accuracy	1998
Anders & Urban (1998)	Explainable Artificial Intelligence (XAI)	Faster Path Integral Calculation	Computational Speed	1998
Tsaih (1999)	General Neural Network basis	Fast approximation of Option Greek	Computational Speed	1999
Garcia & Gencay(2000)	Feed forward neural network model	Reliable hedging Performance	Accuracy	2000
Yao et al. (2000)	Back propagation on Neural Network	Reduced Hedging Error	Accuracy	2000
Dugas et al. ( 2000)	Back propagation on Neural Network	Universal approximation and speeding up the Option Greek Calculation	Computational Speed	2000
Gencay & Qi (2001)	Bayesian regularization over Neural Network.	Reduced Hedging Error	Accuracy	2001
Pagnottoni (2001)	Layered Neural Network	Significant Improvement in Price calculation	Accuracy	2001
Schittenkopf & Dorffner ( 2001)	Semi-Parametric reinforced Learning	More information in Risk neutral Probability Density Calculation	Enhanced Applicability	2001
Montagna et al. (2003)	Route integral with Neural Network Parametrization	Covers Edge Cases like deep In/out of Money Options	Enhanced Applicability	2003
Amilon (2003)	Backward propagation on Neural Network	Better Pricing of Out of the Money options	Enhanced Applicability	2003
Amilon (2003)	Back propagation on Neural Network	Better Pricing than Black Scholes Model	Accuracy	2003
Morelli et al.(2004)	Multi-layer perceptron and radial basis functions.	Fast Numerical Approximation for American Option Greeks	Computational Speed	2004
Lajbcygier (2004)	Constrained Neural Network (CAN)	Improved the accuracy of Option Pricing	Accuracy	2004
Dindar & Marwala (2004)	Conventional multilayer perceptron (MLP) and radial basis functions (RBF)	Better pricing	Accuracy	2004
Bennel & Sutcliffe (2005)	Back propagation on Neural Network	Analytical Approximations	Enhanced Applicability	2005
Amornwattana et al. (2007)	Hybrid neural Network	Equally capable of predicting Option Pricing with historical and Implied Volatility	Enhanced Applicability	2007
Samur & Temur (2009)	Backward propagation on Neural Network	Accelerated Call Option Pricing	Computational Speed	2009
Barunikova & Barunik (2011)	Feed forward neural network model	Improved Pricing	Accuracy	2009
Gradojevic et al. (2009)	Nonparametric modular neural network (MNN)	Better Coverage of Edge Cases	Enhanced Applicability	2009
Liang et al. (2009)	Neural networks (NNs) and support vector regressions (SVRs)	Improved Option Price Forecasting Accuracy	Accuracy	2009
Von Spreckelsen et al. (2014)	Neural Network Approximators	Fast Calculation of Option by Replication and Greek Computation	Computational Speed	2014
Montesdeoca & Niranjan (2016)	Improvement over HLP Model	Reduction in Option Price Prediction	Accuracy	2016
Ferguson & Green (2016)	Deep Re-enforced Learning	High Speed Parameter Calculation	Computational Speed	2016
Yang et al. (2017)	Gated Neural Network	Improved Generalization of Pricing performance	Computational Speed	2017
Huisu Jang & Jaewook Lee (2019)	Generative Bayesian learning model	Higher Prediction performance	Accuracy	2017
Dimitroff et al. (2018)	Supervised deep convolutional neural network	Works on any Moneyness	Enhanced Applicability	2018
Palmer (2019)	Swarm optimization (PSO) and differential evolution (DE)	high Speed Option Sensitivity calculation	Computational Speed	2019
Liu et al. (2019)	ANN as Universal Function Approximator	ANN solver may greatly cut computing time	Computational Speed	2019
Hirsa et al.(2019)	Supervised deep neural networks (DNNs)	Accelerate option pricing tenfold	Computational Speed	2019
Liu et al. (2019)	Calibrated Neural Network (CaNN)	Fast Calibration	Computational Speed	2019
Itkin (2019)	Trained Neural Network	Better replication of Option hedges	Accuracy	2019
Chen & Wan (2019)	Deep Re-enforced Learning	Pricing by Dimensionality Reduction in American Option Pricing	Enhanced Applicability	2019
De Gennaro Aquino & Bernard (2020)	General Neural Network basis	Better management of hedging errors	Accuracy	2020
Zhang et al. (2022)	Bidirectional long short-term memory neural network (BDLSTM)	Reduced Hedging Error	Accuracy	2020
Gasper et al. (2020)	Two Comparative Neural Network Model	Fitting Market price for more edge case scenarios	Enhanced Applicability	2020
Gierjatowicz et al. (2020)	Neural Network constrained Stochastic Differential Equation	Works for both local and Stochastic Volatility Model	Enhanced Applicability	2020
Plooy & Venter (2021)	Bootstrapped Aggregating Ensemble Neural Network	Better Pricing for Options	Accuracy	2021
Germain et al. (2021)	Deep Re-enforced Learning	Increased Pricing scenario	Enhanced Applicability	2021
Carbonneau & Godin ( 2021)	Generic and Tractable Reinforced Learning	Better pricing of Replicating Options	Accuracy	2021
Ratku & Nuemann (2022)	ANN as Alternative to Algorithmic Differentiation	Fast Computation of Option Greeks	Computational Speed	2022
Vadori (2022)	Feedforward neural network model	Faster Path Integral Calculation	Computational Speed	2022
Qian et al. (2022)	GA-BP Neural network	More accurate pricing of Options and Greek Calculations	Accuracy	2022

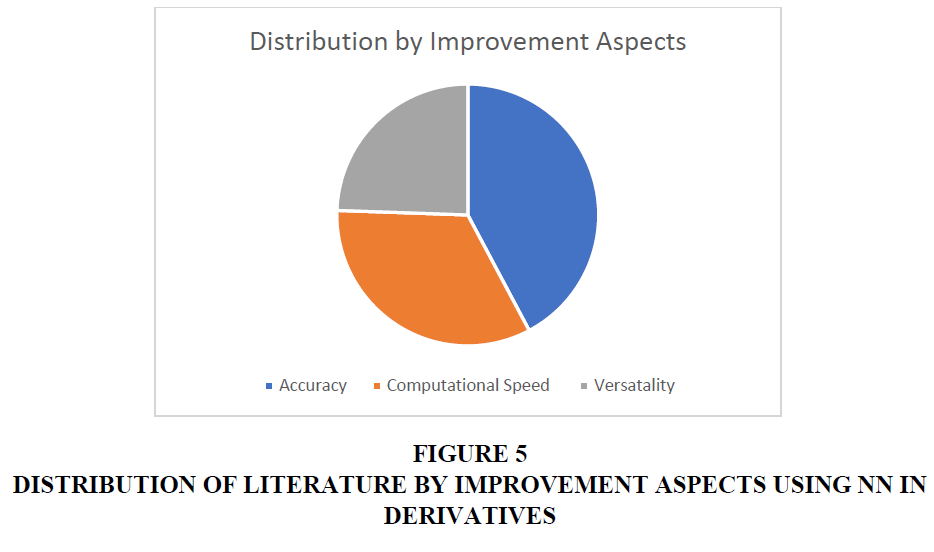
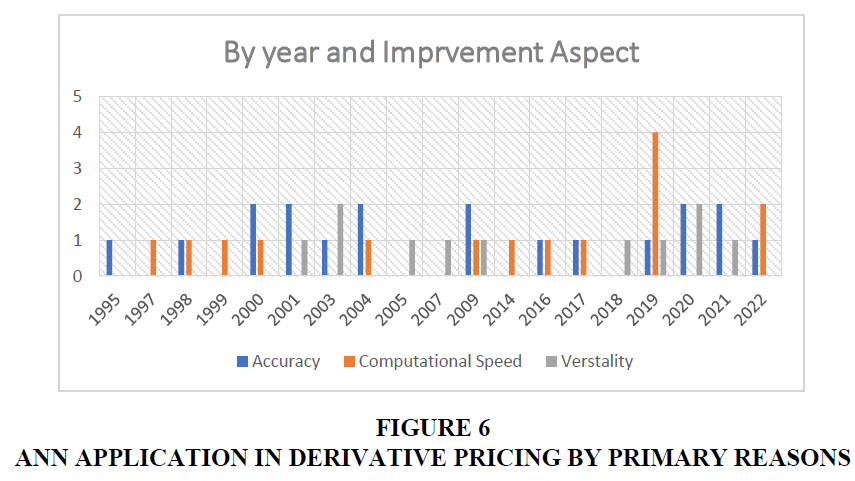
We next placed the application of ANN on a timetable and compared it with the evolution of computational power and computer memories. This allowed us to illustrate that the application of ANN is expanding along with the increasing memory and calculation capability of current computers. This also helps in making predictions about the future, such as the fact that the use of ANN in pricing complicated financial products will continue to increase (Figure 3-6).

Conclusion

In order to overcome the issue of pricing options and to imitate the way in which these financial derivatives do not act in a linear fashion, neural network techniques are being utilized. Large data sets can sometimes have important information extracted from them using a Neural Network. The research that has been done on the use of Artificial Neural Networks (ANN) to the pricing of Financial Derivatives is investigated in this article. In order to gain an understanding of the application of Artificial Neural Networks, we combed through over fifty pertinent scientific publications and compiled a summary of the studies' goals and major findings in order to further indicate the application of ANN into the process of pricing derivatives. We came to the conclusion that ANN has been put to use in the pricing and modeling of financial derivatives on a large scale. Additionally, it has been utilized to compute option Greeks. When utilizing ANN, the computation of option Greeks and other sensitivity occurs much more quickly, with improved accuracy and calibration outcomes. We next placed the application of ANN on a timetable and compared it with the evolution of computational power and computer memories. This allowed us to illustrate that the application of ANN is expanding along with the increasing memory and calculation capability of current computers. This also helps in making predictions about the future, such as the fact that the use of ANN in pricing complicated financial products will continue to increase. Following the findings of this research, it was concluded that Artificial Neural Networks are an effective technique for forecasting the behavior of financial markets around the world. In order to comprehend how Artificial Neural Networks might be applied.

References

Alexandre Carbonneau, A., & Godin, F. (2021). Equal risk pricing of derivatives with deep hedging. Quantitative Finance, 21(4), 593-608.

Indexed at, Google Scholar, Cross Ref

Amilon, H. (2003). A neural network versus black–scholes: A comparison of pricing and hedging performances. Journal of Forecasting, 22(4), 317-335.

Indexed at, Google Scholar, Cross Ref

Amornwattana, S., Enke, D., & Dagli, C.H. (2007). A hybrid option pricing model using a neural network for estimating volatility. International Journal of General Systems, 36(5), 558-573.

Indexed at, Google Scholar, Cross Ref

Anders, U., Korn, O., & Schmitt, C. (1998). Improving the pricing of options: A neural network approach. Journal of forecasting, 17(56), 369-388.

Google Scholar, Cross Ref

Anderson, D., & Ulrych, U. (2022). Accelerated American Option Pricing with Deep Neural Networks. Swiss Finance Institute Research Paper, (22-03).

Indexed at, Google Scholar, Cross Ref

Andreou, P.C., Charalambous, C., & Martzoukos, S.H. (2008). Pricing and trading European options by combining artificial neural networks and parametric models with implied parameters. European Journal of Operational Research, 185(3), 1415-1433.

Indexed at, Google Scholar, Cross Ref

Araque, O., Corcuera-Platas, I., Sánchez-Rada, J.F., & Iglesias, C.A. (2017). Enhancing deep learning sentiment analysis with ensemble techniques in social applications. Expert Systems with Applications, 77, 236-246.

Indexed at, Google Scholar, Cross Ref

Barunıkova, M., & Barunık, J. (2011). Neural networks as a semiparametric option pricing tool.

Google Scholar

Bennell, J., & Sutcliffe, C. (2004). Black–Scholes versus artificial neural networks in pricing FTSE 100 options. Intelligent Systems in Accounting, Finance & Management: International Journal, 12(4), 243-260.

Indexed at, Google Scholar, Cross Ref

Boek, C., Lajbcygier, P., Palaniswami, M., & Flitman, A. (1995). A hybrid neural network approach to the pricing of options. In Proceedings of ICNN'95-International Conference on Neural Networks 2, 813-817.

Indexed at, Google Scholar, Cross Ref

Boyacioglu, M.A., Kara, Y., & Baykan, O.K. (2009). Predicting bank financial failures using neural networks, support vector machines and multivariate statistical methods: A comparative analysis in the sample of savings deposit insurance fund (SDIF) transferred banks in Turkey. Expert Systems with Applications, 36(2), 3355-3366.

Indexed at, Google Scholar, Cross Ref

Brooks, C., Hoepner, A.G., McMillan, D., Vivian, A., & Wese Simen, C. (2019). Financial data science: The birth of a new financial research paradigm complementing econometrics? The European Journal of Finance, 25(17), 1627-1636.

Indexed at, Google Scholar, Cross Ref

Burrell, P.R., & Folarin, B.O. (1997). The impact of neural networks in finance. Neural Computing & Applications, 6(4), 193-200.

Indexed at, Google Scholar, Cross Ref

Carverhill, A.P., & Cheuk, T.H. (2003). Alternative neural network approach for option pricing and hedging. Available at SSRN 480562.

Indexed at, Google Scholar, Cross Ref

Cavalcante, R.C., Brasileiro, R.C., Souza, V.L., Nobrega, J.P., & Oliveira, A.L. (2016). Computational intelligence and financial markets: A survey and future directions. Expert Systems with Applications, 55, 194-211.

Indexed at, Google Scholar, Cross Ref

Chen, F., & Sutcliffe, C. (2012). Pricing and hedging short sterling options using neural networks. Intelligent Systems in Accounting, Finance and Management, 19(2), 128-149.

Indexed at, Google Scholar, Cross Ref

Coakley, J.R., & Brown, C.E. (2000). Artificial neural networks in accounting and finance: Modeling issues. Intelligent Systems in Accounting, Finance & Management, 9(2), 119-144.

Indexed at, Google Scholar, Cross Ref

De Gennaro Aquino, L., & Bernard, C. (2020). Bounds on multi-asset derivatives via neural networks. International Journal of Theoretical and Applied Finance, 23(08), 2050050.

Indexed at, Google Scholar, Cross Ref

Dindar, Z.A., & Marwala, T. (2004). Option pricing using a committee of neural networks and optimized networks. In 2004 IEEE International Conference on Systems, Man and Cybernetics (IEEE Cat. No. 04CH37583) (Vol. 1, pp. 434-438). IEEE.

Google Scholar, Cross Ref

Du Plooy, R., & Venter, P.J. (2021). A comparison of artificial neural networks and bootstrap aggregating ensembles in a modern financial derivative pricing framework. Journal of Risk and Financial Management, 14(6), 254.

Indexed at, Google Scholar, Cross Ref

Dugas, C., Bengio, Y., Bélisle, F., Nadeau, C., & Garcia, R. (2000). Incorporating second-order functional knowledge for better option pricing. Advances in neural information processing systems, 13.

Google Scholar

Fadlalla, A., & Lin, C.H. (2001). An analysis of the applications of neural networks in finance. Interfaces, 31(4), 112-122.

Indexed at, Google Scholar, Cross Ref

Feldman, K., & Kingdon, J. (1995). Neural networks and some applications to finance. Applied Mathematical Finance, 2(1), 17-42,

Google Scholar, Cross Ref

Ferguson, R., & Green, A. (2018). Deeply learning derivatives. arXiv preprint arXiv:1809.02233.

Google Scholar, Cross Ref

Garcia, R., & Gençay, R. (2000). Pricing and hedging derivative securities with neural networks and a homogeneity hint. Journal of Econometrics, 94(1-2), 93-115.

Indexed at, Google Scholar, Cross Ref

Gaspar, R.M., Lopes, S.D., & Sequeira, B. (2020). Neural network pricing of american put options. Risks, 8(3), 73.

Indexed at, Google Scholar, Cross Ref

Gençay, R., & Qi, M. (2001). Pricing and hedging derivative securities with neural networks: Bayesian regularization, early stopping, and bagging. IEEE Transactions on Neural Networks, 12(4), 726-734.

Indexed at, Google Scholar, Cross Ref

Germain, M., Pham, H., & Warin, X. (2021). Neural networks-based algorithms for stochastic control and PDEs in finance. arXiv preprint arXiv:2101.08068.

Google Scholar, Cross Ref

Gierjatowicz, P., Sabate-Vidales, M., Šiška, D., Szpruch, L., & Žurič, Ž. (2020). Robust pricing and hedging via neural SDEs. arXiv preprint arXiv:2007.04154.

Indexed at, Google Scholar, Cross Ref

Gilbert, E.W., Krishnaswamy, C.R., & Pashley, M.M. (2000). Neural Network Applications in Finance: A Practical Introduction.

Google Scholar

Gradojevic, N., Gençay, R., & Kukolj, D. (2009). Option pricing with modular neural networks. IEEE transactions on neural networks, 20(4), 626-637.

Indexed at, Google Scholar, Cross Ref

Grohs, P., Hornung, F., Jentzen, A., & Von Wurstemberger, P. (2018). A proof that artificial neural networks overcome the curse of dimensionality in the numerical approximation of Black-Scholes partial differential equations. arXiv preprint arXiv:1809.02362.

Indexed at, Google Scholar, Cross Ref

Haykin, S. (1996). Neural networks expand SP's horizons. IEEE Signal Processing Magazine, 13(2), 24-49.

Indexed at, Google Scholar, Cross Ref

Haykin, S. (2009a). Neural networks and learning machines, 3/E. Pearson Education India.

Haykin, S., & Network, N. (2004). A comprehensive foundation. Neural networks, 2, 41.

Google Scholar

Herrmann, R., & Narr, A. (1996). Neural networks and the evaluation of derivatives: some insights into the implied pricing mechanism of german stock index options. Institut für Entscheidungstheorie und Unternehmensforschung.

Indexed at, Google Scholar

Hirsa, A., Karatas, T., & Oskoui, A. (2019). Supervised deep neural networks (DNNs) for pricing/calibration of vanilla/exotic options under various different processes. arXiv preprint arXiv:1902.05810.

Indexed at, Google Scholar, Cross Ref

Horvath, B., Muguruza, A., & Tomas, M. (2021). Deep learning volatility: a deep neural network perspective on pricing and calibration in (rough) volatility models. Quantitative Finance, 21(1), 11-27.

Indexed at, Google Scholar, Cross Ref

Huang, J., Chai, J., & Cho, S. (2020). Deep learning in finance and banking: A literature review and classification. Frontiers of Business Research in China, 14(1), 1-24.

Indexed at, Google Scholar, Cross Ref

Huang, W., Lai, K.K., Nakamori, Y., Wang, S., & Yu, L. (2007). Neural networks in finance and economics forecasting. International Journal of Information Technology & Decision Making, 6(01), 113-140.

Indexed at, Google Scholar, Cross Ref

IMF (2018), Eleventh Meeting of the IMF Committee on Balance of Payments Statistics, Washington, D.C., October 21–23, 1998.

Itkin, A. (2019). Deep learning calibration of option pricing models: some pitfalls and solutions. arXiv preprint arXiv:1906.03507.

Indexed at, Google Scholar, Cross Ref

Jahnavi, M (2017). Introduction to Neural Networks, Advantages and Applications, towards Data Science.

Google Scholar

Jang, H., & Lee, J. (2019). Generative Bayesian neural network model for risk-neutral pricing of American index options. Quantitative Finance, 19(4), 587-603.

Indexed at, Google Scholar, Cross Ref

Lajbcygier, P. (2004). Improving option pricing with the product constrained hybrid neural network. IEEE Transactions on Neural Networks, 15(2), 465-476.

Indexed at, Google Scholar, Cross Ref

Liang, X., Zhang, H., Xiao, J., & Chen, Y. (2009). Improving option price forecasts with neural networks and support vector regressions. Neurocomputing, 72(13-15), 3055-3065.

Indexed at, Google Scholar, Cross Ref

Liu, S., Borovykh, A., Grzelak, L. A., & Oosterlee, C. W. (2019). A neural network-based framework for financial model calibration. Journal of Mathematics in Industry, 9(1), 1-28.

Indexed at, Google Scholar, Cross Ref

Liu, S., Oosterlee, C.W., & Bohte, S.M. (2019). Pricing options and computing implied volatilities using neural networks. Risks, 7(1), 16.

Indexed at, Google Scholar, Cross Ref

MacBeth, J. D., & Merville, L. J. (1979). An empirical examination of the Black-Scholes call option pricing model. The journal of finance, 34(5), 1173-1186.

Indexed at, Google Scholar, Cross Ref

Malliaris, M., & Salchenberger, L. (1993). A neural network model for estimating option prices. Applied Intelligence, 3(3), 193-206.

Indexed at, Google Scholar, Cross Ref

Marr, D. (1975). Approaches to Biological Information Processing: Physics and Mathematics of the Nervous System. Proceedings of a summer school, Trieste, Italy, Aug. 1973. Science, 190(4217), 875-876.

Indexed at, Google Scholar, Cross Ref

McClelland, J. L., Rumelhart, D. E., & Hinton, G. E. (1986). The appeal of parallel distributed processing. MIT Press, Cambridge MA, 3, 44.

Google Scholar

McCulloch, W. S., & Pitts, W. (1943). A logical calculus of the ideas immanent in nervous activity. The bulletin of mathematical biophysics, 5(4), 115-133.

Indexed at, Google Scholar, Cross Ref

Montagna, G., Morelli, M., Nicrosini, O., Amato, P., & Farina, M. (2003). Pricing derivatives by path integral and neural networks. Physica A: Statistical Mechanics and its Applications, 324(1-2), 189-195.

Indexed at, Google Scholar, Cross Ref

Montesdeoca, L., & Niranjan, M. (2016). Extending the feature set of a data-driven artificial neural network model of pricing financial options. In 2016 IEEE symposium series on computational intelligence (SSCI), 1-6.

Google Scholar, Cross Ref

Morelli, M. J., Montagna, G., Nicrosini, O., Treccani, M., Farina, M., & Amato, P. (2004). Pricing financial derivatives with neural networks. Physica A: Statistical Mechanics and its Applications, 338(1-2), 160-165.

Indexed at, Google Scholar, Cross Ref

Pagnottoni, P. (2019). Neural network models for Bitcoin option pricing. Frontiers in Artificial Intelligence, 2, 5.

Indexed at, Google Scholar, Cross Ref

Personnaz, L., Guyon, I., & Dreyfus, G. (1986). Collective computational properties of neural networks: New learning mechanisms. Physical Review A, 34(5), 4217.

Indexed at, Google Scholar, Cross Ref

Palmer, S. (2019). Evolutionary algorithms and computational methods for derivatives pricing (Doctoral dissertation, UCL (University College London)).

Indexed at, Google Scholar, Cross Ref

Qian, L., Zhao, J., & Ma, Y. (2022). Option Pricing Based on GA-BP neural network. Procedia Computer Science, 199, 1340-1354.

Indexed at, Google Scholar, Cross Ref

Rahmanifard H, Plaksina T. Application of artificial intelligence techniques in the petroleum industry: a review. Artificial Intelligence Review. 2019 Dec;52(4):2295-318.

Indexed at, Google Scholar, Cross Ref

Ratku, A., & Neumann, D. (2022). Derivatives of feed-forward neural networks and their application in real-time market risk management. OR Spectrum, 1-19.

Indexed at, Google Scholar, Cross Ref

Riyazahmed, D.K. (2021). Neural Networks in Finance: A Descriptive systematic review. Indian journal of Banking and Finance, 5(2), 1-27.

Google Scholar, Cross Ref

Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review, 65(6), 386.

Indexed at, Google Scholar, Cross Ref

Samur, Z.I., & Temur, G.T. (2009). The use of artificial neural network in option pricing: the case of S&P 100 index options. World Academy of Science, Engineering and Technology, 54, 326-331.

Google Scholar

Schittenkopf, C., & Dorffner, G. (2001). Risk-neutral density extraction from option prices: improved pricing with mixture density networks. IEEE Transactions on Neural Networks, 12(4), 716-725. 5.

Indexed at, Google Scholar, Cross Ref

Smith Jr, C. W. (1976). Option pricing: A review. Journal of Financial Economics, 3(1-2), 3-51.

Indexed at, Google Scholar, Cross Ref

Taylor, S.J. (1994). Modeling stochastic volatility: A review and comparative study. Mathematical finance, 4(2), 183-204.

Google Scholar, Cross Ref

Tsaih, R. (1999). Sensitivity analysis, neural networks, and the finance. In IJCNN'99. International Joint Conference on Neural Networks. Proceedings (Cat. No. 99CH36339) (Vol. 6, pp. 3830-3835). IEEE.

Indexed at, Google Scholar, Cross Ref

Vadori, N. (2022). Calibration of Derivative Pricing Models: a Multi-Agent Reinforcement Learning Perspective. arXiv preprint arXiv:2203.06865.

Indexed at, Google Scholar, Cross Ref

Vellido, A., Lisboa, P.J., & Vaughan, J. (1999). Neural networks in business: a survey of applications (1992–1998). Expert Systems with applications, 17(1), 51-70..

Indexed at, Google Scholar

Von Spreckelsen, C., von Mettenheim, H.J., & Breitner, M.H. (2014). Real‐time pricing and hedging of options on currency futures with artificial neural networks. Journal of Forecasting, 33(6), 419-432.

Indexed at, Google Scholar, Cross Ref

Wang, D., He, H., & Liu, D. (2017). Adaptive critic nonlinear robust control: A survey. IEEE transactions on cybernetics, 47(10), 3429-3451.

Indexed at, Google Scholar, Cross Ref

Wong, B.K., & Selvi, Y. (1998). Neural network applications in finance: A review and analysis of literature (1990–1996). Information & Management, 34(3), 129-139.

Indexed at, Google Scholar, Cross Ref

Yadav, K. (2021). Formulation of a rational option pricing model using artificial neural networks. In Southeast Conference. 1-8. IEEE.

Indexed at, Google Scholar, Cross Ref

Yang, Y., Zheng, Y., & Hospedales, T. (2017). Gated neural networks for option pricing: Rationality by design. In Proceedings of the AAAI Conference on Artificial Intelligence, 31,(1).

Indexed at, Google Scholar, Cross Ref

Yao, J., Li, Y., & Tan, C.L. (2000). Option price forecasting using neural networks. Omega, 28(4), 455-466.

Indexed at, Google Scholar, Cross Ref

Zapart, C.A. (2003). Beyond Black–Scholes: A neural networks-based approach to options pricing. International Journal of Theoretical and Applied Finance, 6(05), 469-489.

Indexed at, Google Scholar, Cross Ref

Zhang, F., Fleyeh, H., & Bales, C. (2022). A hybrid model based on bidirectional long short-term memory neural network and Catboost for short-term electricity spot price forecasting. Journal of the Operational Research Society, 73(2), 301-325.

Indexed at, Google Scholar, Cross Ref

Received: 19-Dec-2022, Manuscript No. AMSJ-22-13031; Editor assigned: 20-Dec-2022, PreQC No. AMSJ-22-13031(PQ); Reviewed: 24-Dec-2022, QC No. AMSJ-22-13031; Revised: 01-Feb-2023, Manuscript No. AMSJ-22-13031(R); Published: 17-Mar-2023