Keywords

Social Economic, Supply Chains, Social welfare.

Introduction

Social sustainability, as one of the three pillars of the sustainability, has observed an increasing impact on supply chain management research. To describe social sustainability, UNDSD (the United Nations Division for Sustainable Development) has established a framework in an effort to measure sustainability. Within the social sustainability dimension, it has six themes: Equity, health, education, housing, security and population. Hediger (2000) proposed a sustainability-based social value function to address the social welfare function on a set of sustainability constraints. Lee and Whang (2002) examined the impact of a secondary market on supply chain, including the welfare of the supply chain. Tsuda and Takaoka (2006) proposed a comprehensive sustainability index, named “gross social feel-good” index. The index consists of six components, including environment, economy, safety, health, comfort and happiness. Cruz and Wakolbinger (2008) simply adopted cost functions for social sustainability activities. Carter and Rogers (2008) provided a comprehensive literature review on sustainability and a conceptual introduction of it to supply chain management. Hutchins and Sutherland (2008) discussed certain metrics, indicators and frameworks relative to evaluate social sustainability for supply chains; however, none of them are quantitative. Cowan (2007) studied the welfare effects when demand in one market is an additively shifted version of demand in the other market. The book by Fleurbaey and Blanchet (2013) explored indictors on the ethical consideration and economic theory towards measuring welfare and assessing sustainability.

Overall, it is not quite clear what exactly social sustainability consists of and how to measure social sustainability. In our works, we employ the classic concept of deadweight loss from economics to quantify the loss in social surplus, which is the amount of welfare or utility that a society has gained from the consumption of all goods and services. We believe social surplus and deadweight loss can be an integral component of social sustainability, particularly from the supply chain perspective. Social welfare is then captured by deadweight loss.

When firms are concerned with their respective supply chains alone, it is probably a good idea to integrate the competing channels. However, when multiple channels are competing with each other, how will the integration of individual channel affect social welfare? Will consumers be better off or worse off? These questions largely remain unanswered and are little explored in literature. The intent of this paper is to investigate the social welfare issue in an industry consisting of two competing channels.

To that end, we consider an industry consisting of two competing channels, which can be either decentralized or vertically integrated. In a decentralized channel, there is one upstream firm (called manufacturer hereafter) and one downstream firm (called retailer hereafter). Each firm makes its decision independently to maximize its own profit. According to different degrees of vertical integration across different channels, we thus have the following four industry channel configurations. We call the industry with two decentralized channel DD configuration or decentralized configuration. Similarly, the industry with two integrated channel is called II configuration or integrated configuration. Lastly, the industry with one decentralized channel and one integrated channel is called mixed configuration. Mixed configuration can be either DI or ID. In the DI configuration, channel 1 is decentralized whereas channel 2 is integrated. In the ID configuration, channel 1 is integrated whereas channel 2 is decentralized. As a benchmark, we also consider a case of fully centralized industry, i.e., one entity makes all decisions to maximize the profit of the entire industry.

We calculate equilibrium prices, quantities and deadweight losses for different industry configurations and then study the issue of social welfare as well as investigate the impact of demand asymmetry, differentiation and vertical integration.

Our key findings are: (1) Monopoly does not always hurt social welfare; (2) having equally matched competing channels may or may not be socially beneficial, depending on the industry configurations.

The remainder of this paper is organized as follows. Section 2 reviews related literature. Our model, as well as all optimal and equilibrium results of each configuration, is described in Section 3. Section 4 analyses results from Section 3. The paper is concluded in Section 5.

Related Literature

Many recent research topics on sustainable supply chain are introduced in the special issue in the Journal of Cleaner Production (edited by Seuring, Sarkis, Müller, & Rao, 2008).

The industry configurations studied in this paper are similar to those in McGuire & Staelin (1983). They find that when retail competition between two substitutable products is sufficiently high, two manufacturers prefer selling via wholesale price contract to integrating their respective channels. Moorthy (1988) later identified conditions on the game rule and demand function in order for decentralization to be an equilibrium strategy. A more recent work, Wu & Mallik (2010), extended this line of research to industry configurations in which retailers can carry competing products. This stream of research focuses on strategic interactions between and within competing channels. They have shown that all the industry configurations studied in this paper (DD, ID/DI and II) can be equilibrium gaming results under certain conditions. Built upon these results, we can reasonably assume that the industry configurations are exogenously given and focus on the issue of social welfare in this paper.

O’Brien & Shatter (1994) considered a market in which a single manufacturer produces a product and sells it to two competing retailers. They examined the welfare effects of Robinson-Patman Act and found that forbidding discriminatory discounts leads to all retailers paying higher prices and thus charging higher prices in retail markets. Although they studied the welfare issue, the differences between their work and ours are apparent. We consider two manufacturers and two competing products. Since each manufacturer has only one distribution channel, wholesale price discrimination issue does not exist in our model. We, instead, examine the impacts of vertical integration, demand asymmetry and differentiation on social welfare.

Inderst & Shaffer (2009) considered a monopolistic supplier with two asymmetric retailers. They examined the optimal discriminatory two-part tariffs of the supplier and found that larger retailer obtains lower wholesale price, which increases allocative efficiency. The demand asymmetry in our model is analogous to the retailer asymmetry in Inderst and Shaffer (2009). Instead of examining the effects of discriminatory pricing, which is not possible in our setting, we consider two manufacturers, each with a competing product and a single channel. Social welfare is then studied with vertical integration.

Model

As mentioned earlier, the DD, DI/ID and II industry configurations are assumed to be exogenously and they have been proven to be equilibrium outcome. This assumption simplifies the analyses and allows us to stay focused on studying social welfare issue. In addition, we will use the fully centralized configuration as the benchmark case, denoted by B.

Demand Functions, Deadweight Loss and Social Welfare

We adopt a demand function similar to that in Raju et al. (1995) and that in Indest and Shaffer (2009). Unlike Raju et al. (1995), we capture demand asymmetry in our demand function as follows:

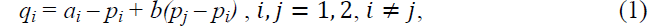
where q_i represents the demand for product i, p_i is the retail price of product i. Note that ai describes the demand potential of product i. Without loss of generality, we assume that a₁>a₂, which captures demand asymmetry. Demand asymmetry is similar to retailer asymmetry in Inderst and Shaffer (2009). The market potential of product 1 (a1) is larger either because product 1 is more superior or because channel 1 is more efficient. Furthermore, we let a2=ka1, where k is a scalar between zero and one. By exploring the impact of k, we can understand how demand asymmetry affects social welfare.

Parameter b captures the demand sensitivity to a price gap between the two products. In some cases, such as Wu and Mallik (2010), b is interpreted as the degree of product substitutability and horizontal competition. When b=0, two products are completely different. The larger the b is, the more similar or substitutable these two products are. As a consequence, demand of each product becomes more sensitive to the price difference. In some other cases, such as Inderst and Shaffer (2009), b is an indicator of retail differentiation (or more generally, channel differentiation). When b=0, two retailers reach perfect differentiation. As b increases, two retailers become more similar. The degree of differentiation can be attributed to the differences between either the two products or the two retailers. We do not distinguish such differences. Thus, we interpret b as an indicator of degree of horizontal competition or differentiation, whether it is a result of product difference or retail differentiation. The larger b is, the less differentiated the two products/channels are; and thus the horizontal competition is more intense.

To investigate social welfare, we employ the concept of deadweight loss from classic economics. In Figure 1, we depict the demand function of product 1, conditional on the price of product 2. As easily seen from Figure 1, the deadweight loss in the market of product 1, denoted by L₁, is as follows:

Figure 1:Consumer?s Surplus, Profit And Deadweight Loss In Market Of Product 1.

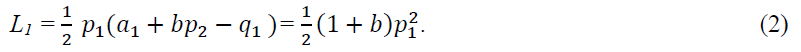
Similarly, the total deadweight loss, L, equal to the sum of L₁ and L₂ (deadweight loss in the market of product 2) is as follows:

Equipped with Equation (3), we can examine how demand asymmetry, differentiation (or degree of horizontal competition) and vertical integration affect social welfare.

Equilibrium Outcomes

We first introduce some notations. If channel i (i=1 or 2) is decentralized, let wi be the wholesale price of product i charged by the decentralized manufacturer i. Let p_i be the retail price of product i charged by the decentralized retailer i. If channel i (i=1 or 2) is integrated, pi is the retail price of product i charged by the integrated channel i. Asterisk “*” indicates equilibrium or optimal values.

For any given industry configuration, we use a non-cooperative game to examine the equilibrium prices and quantities. In the DD configuration, two manufactures determine their respective wholesale prices first. And then two retailers select their respective retail prices to maximize their own profits. In mixed configurations, ID for instance, the decentralized manufacturer chooses its wholesale price, w₂, first. Next, note that there is no wholesale price in a vertically integrated chain. Channel 1 (vertically integrated chain) and the decentralized retailer will decide their respective retail prices. In the II configuration, two chains set their respective retail prices. At each stage of the game, all the decisions are made independently and simultaneously. This assumption is standard in conventional non-cooperative games. To simplify analyses, we assume that the unit production and retailing cost is zero. Unit production and retailing cost does not qualitatively affect the results of this paper.

We solve the above games backward. It is easy to verify that a unique equilibrium exists in each game. The equilibrium results are summarized in Tables 1-4 below.

Table 1: Equilibrium Values In The Benchmark Case And The Ii Configuration
	Benchmark (B)	Two Vertically Integrated Channels (II)
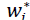	NA	NA

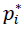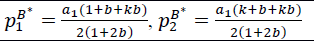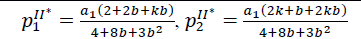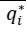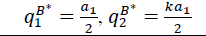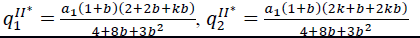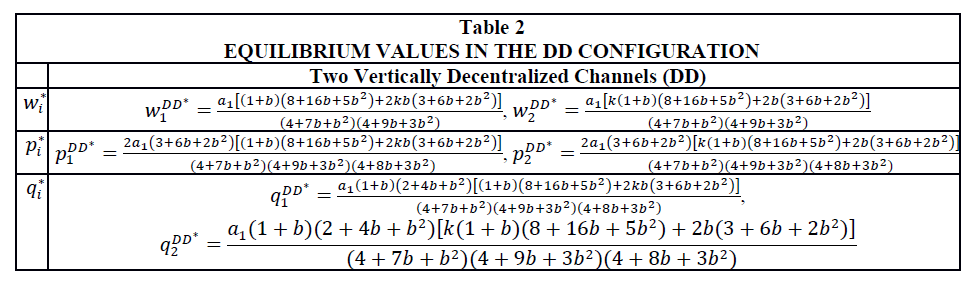
Results and Analyses

In this section, we look into the effects of vertical integration, differentiation and demand asymmetry on deadweight losses.

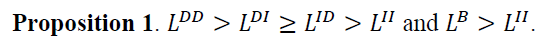
Proposition 1 implies a few interesting results. The most significant result is that 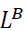could be less than 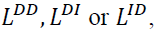depending on the values of k and b. Although horizontal integration seems to hurt social welfare since 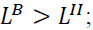but a monopoly is not necessary socially worse than the DD, DI or ID configurations. Note that the DD configuration has the most degree of both vertical and horizontal competition. Interestingly, the DD configuration yields the most deadweight loss among all five configurations, regardless of the values of k and b (Appendix 2).

In addition, as the degree of vertical integration increases, deadweight losses decrease. That is, vertical integration is socially beneficial based on social welfare and deadweight loss. Lastly, if between the two competing channels of an industry, a social planner can only choose to vertically integrate one, then she ought to integrate the more dominant channel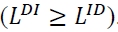

Generally, vertical competition drives retail price up whereas horizontal competition drives price down. Therefore, it is not surprising to see deadweight losses decrease as degree of vertical integration increases. With higher degree of vertical integration, there is less vertical competition. In the benchmark case of monopoly, both vertical and horizontal competition is eliminated. But the competing nature between two products remains, in the form of internal cannibalization. This may be the reason why the monopoly could possibly result in less deadweight loss than the DD, DI and ID configuration, but not the II configuration.

Next, we look into the effect of k on social welfare. Recall that 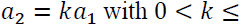1 That is, channel 1 is more dominant in a market than channel 2. The larger the k is, the more equal the two channels are. However, as k increases, the market size for product 2 also increases while the market size for product 1 remains the same. It is not a surprise to see all the absolute deadweight losses, as defined in Equation (3), increase in k. It is also obvious that the absolute consumers’ surplus increases in k. A much more important result will be about how the relative deadweight losses change as k changes. To that end, we define the area under the demand curve in Figure 1 to be the total welfare associated with market for product 1, denoted by TW1. From Figure 1, TW1 is the sum of consumers’ surplus in market 1, channel 1’s profits and deadweight loss L₁. Algebraically,

We further define the relative deadweight loss to be as follows:

From the definitions of and, we have the following:

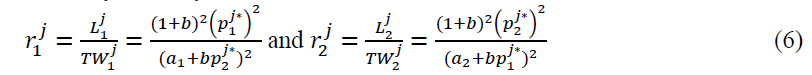
Proposition 2 below summarizes how relative market size (k) will affect deadweight losses and social welfare both in absolute and relative sense.

Proposition 2.

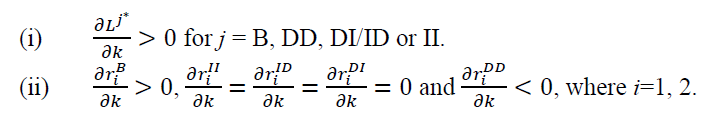
Proposition 2 says that as the potential market sizes of two channels become more equal, the absolute deadweight losses increase in all five configurations. More interestingly and importantly, however, proposition 2 paints a drastically different picture with respect to relative deadweight losses (Appendix 2).

In the benchmark case where the industry is fully vertically and horizontally integrated, the relative deadweight loss increases in k. In other words, when two products become more equal in market size, the social welfare suffers both in absolute and relative sense. In the DI, ID and II configurations, however, k value has no effect on relative deadweight losses. It implies that consumers’ surplus, channel’s profits, as well as absolute deadweight loss will change proportionally as k changes. In the DD configuration, on the other hand, the relative deadweight loss decreases in k. That is, when both horizontal and vertical competition coexists, the more equally matched the two channels are, the more socially beneficial it is.

It appears that the industry structure, in terms of both vertical and horizontal competition, plays a crucial role in how demand asymmetry between the two channels (as described by k) would affect social welfare. Proposition 2 indicates that we must be extremely careful to examine the possible welfare effects of any anti-trust case: Sometimes equally matched opponents are socially beneficial; some other times they are not.

Conclusion

This paper adopts a stylized model of an industry consisting of two competing channels. Each channel, either vertically integrated or decentralized, produces and sells one of the two competing products. Under such a framework, we study the issue of social welfare. In particular, we look into how vertical competition, horizontal differentiation and demand asymmetry would affect social welfare. The key contribution of this work is as follows.

First, we have found that: (i) Vertical integration (or lack of vertical competition) is, in general, socially beneficial; and (ii) horizontal integration (or lack of horizontal competition), against common belief, does not necessarily hurt social welfare. Indeed, as more competing channels are vertically integrated, the deadweight losses decrease; and thus social welfare increases. This result may not be very surprising. However, a pure monopoly, defined as an industry controlled by one entity, could be more socially beneficial than many other industry configurations. In fact, depending on the degrees of demand asymmetry (described by k) and channel differentiation (described by b), the monopoly could result in less deadweight loss than the DD, ID or DI configurations, in which there is higher degree of both horizontal and vertical competition. One exception is, regardless of the values of k and b, the II configuration is always the most socially beneficial among all five industry configurations considered.

Second, the effects of demand asymmetry (k) on social welfare differ drastically, depending on the industry configurations. When the industry is fully controlled by a monopolist, the social welfare gets worse as demand asymmetry decreases; when one or both channels are vertically integrated, the demand asymmetry does not affect the relative deadweight losses at all; and when both channels are decentralized (the DD configuration), the social welfare suffers more as demand asymmetry increases. In other words, when both vertical and horizontal competition present, it is socially beneficial to have equally matched competing channels.

Our paper has identified many interesting observations; it is not the purpose of this study to deeply investigate the causes. Due to the complexness of the situations where horizontal and vertical competition coexists, it is probably worthwhile further investigating the issues and seeking explanations in separate research projects. Furthermore, it will be very intriguing to model an actual industry and study how vertical and horizontal competition would actually affect social welfare.

Appendix

Proof of Proposition 1

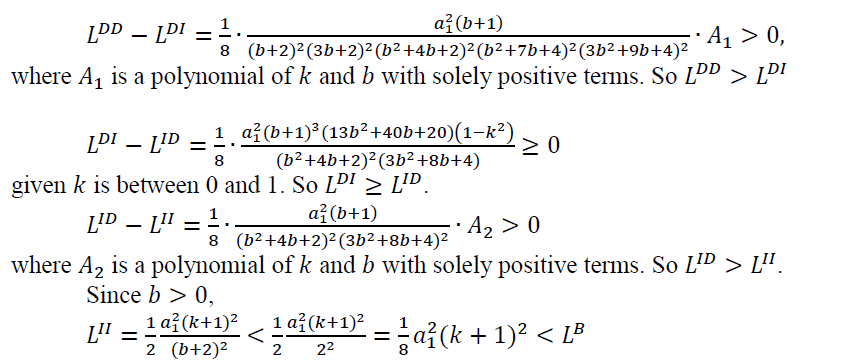
Proof of Proposition 2

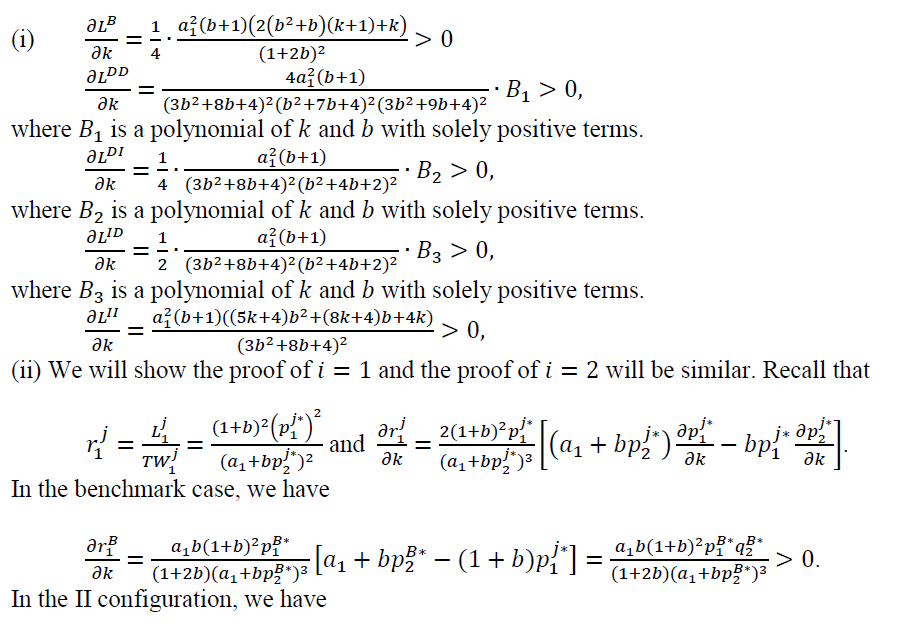
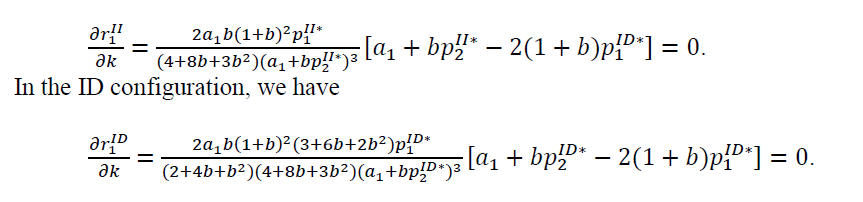
It is equal to zero because 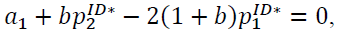which comes from the 1^st-order conditions of the profit maximization problem of each channel.

To prove the result with respect to the DI and DD configurations, we define the following to simplify all the expressions:

References

1. Carter, C.R. & Rogers, D.S. (2008). A framework of sustainable supply chain management: Moving toward new theory. International Journal of Physical Distribution & Logistics Management, 38(5), 360-387.
2. Cowan, S. (2007). The welfare effects of third-degree price discrimination with nonlinear demand functions. RAND Journal of Economics, 38(2), 419-428.
3. Cruz, J.M. & Wakolbinger, T. (2008). Multiperiod effects of corporate social responsibility on supply chain networks, transaction costs, emissions and risk. International Journal of Production Economics, 116, 61-74.
4. Fleurbaey, M. & Blanchet, D. (2013). Beyond GDP: Measuring welfare and assessing sustainability. Oxford University Press.
5. Hediger, W. (2000). Sustainable development and social welfare. Ecological Economics. 32(3), 481-492.
6. Hutchins, M. & Sutherland, J.W. (2008). An exploration of measures of social sustainability and their application to supply chain decisions. Journal of Cleaner Production, 16(15), 1688-1698.
7. Inderst, R. & Shaffer, G. (2009). Market power, price discrimination and allocative efficiency in intermediate-goods markets. RAND Journal of Economics, 40(4), 658-672.
8. Lee, H. & Whang, S. (2002). The impact of the secondary market on the supply chain. Management Science, 48(6), 719-731.
9. McGuire, T.W. & Staelin, R. (1983). An industry equilibrium analysis of downstream vertical integration. Marketing Science, 2(2), 161-191.
10. Moorthy, K.S. (1988). Strategic decentralization in channels. Marketing Science, 7(4), 335-355.
11. O?Brian, P.D. & Shaffer, G. (1994). The welfare effects of forbidding discriminatory discounts: A secondary line analysis of Robinson-Patman. Journal of Law, Economics & Organization, 10(2), 296-318.
12. Raju, J.S., Sethuraman, R. & Dhar, S.K. (1995). The introduction and performance of store brands. Management Science, 41(6), 957-978.
13. Tsuda, M. & Takaoka, M. (2006). Novel evaluation method for social sustainability affect by using ICT services. International Life Cycle Assessment & Management Conference, Washington, DC.
14. Wu, C. & Mallik, S. (2010). Cross sales in supply chains: An equilibrium analysis. International Journal of Production Economics, 126(2), 158-167.
15. Zhang, F. (2011). Supply Chain Coordination. In Wiley Encyclopedia of Operations Research and Management Science. Wiley.