Keywords

Inflation, Forecasting, India, Consumer Price Index, ARIMA.

JEL Classifications

C53, E31, E37, E47.

Introduction

Inflation is possibly one of the most well-recognized and recallable indicators for controlling and judging economic wellbeing of a country (Enke & Mehdiyev, 2014). Uncontrolled inflation may negatively affect the purchasing power of the currency. Uncontrolled inflation also affects the investment scenario of the country, results in project cost over-run, enhances income disparity, and culminates difficulty in financial intervention (Hurtado et al., 2013). It is therefore important to forecast the expected inflation trend. An accurate prediction of inflation is important for making sound policy decisions (Mcnelis & Mcadam, 2004). In this study, we consider CPI as an important reflector of inflationary trends in economy. CPI may be considered as a summary statistic for frequency distribution of relative prices (Kharimah et al., 2015). CPI measures the changes in general level of prices of a group of commodities (Manga, 1977; Subhani & Panjwani, 2009). The forecasting of CPI is important in the sense that it helps in developing more accurate investment and savings decisions, resulting into better resource utilization and economic stability (Enke & Mehdiyev, 2014). The Urjit Patel led committees report (2013) suggested using CPI as nominal anchor for targeting inflation under monetary policy. This is useful, because CPI very closely follows the cost of living and also the expectations of inflation.

In this paper, the objective is to create a forecasting model of CPI, where CPI is an indicator of inflation in India. The rest of the paper is arranged as follows. The section “Literature review” provide the past empirical literature on forecasting of inflation. Section “Data and period of study” underlines the data and period of study. Section “Empirical results” presents the estimated results, and the “discussions” section represents the factors that may impact the future movement of Indian inflation rate and the economic interpretations. Section “Conclusion and policy implications” concludes the study by summarizing the outcome, limitations, and scope for further research.

Literature Review

Forecasting of inflation is a popular and important topic to explore among researchers. The Irish inflation was forecasted by Meyler et al. (1998) using ARIMA model. The Finnish inflation was forecasted and modeled by Kock & Teravirta (2013) by using Artificial Neural Network. The paper used a dataset ranging from March 1960 to December 2009. It also established that direct forecasts are more accurate than their recursive counterparts. The CPI of Malaysia was analyzed by Kharimah (2015) using ARIMA. The study reveals that ARIMA (1,1,0) is possibly the best model to forecast CPI in Malaysia.

Owusu (2010) created a forecasting model on monthly inflation using ARIMA. The study divided the time series into two-time frames. The first one, considers inflation rates from 1990 – 2000, and the second sub-period considers 2001-2009. The study shows ARIMA (1,2,2) is the best inflation model for 1990-2000. And the ARIMA (2,2,1) is the best model for the period 2001 – 2010.

Milo (2012) confirms a positive relationship between the monetary financing of government deficits and money base growth in Albania, Bulgaria, and Romania. Nguyen (2015) discussed the effects of broad money M2 supply and fiscal deficit on inflation in Asian economies e.g. Indonesia, Malaysia, Cambodia, Bangladesh, Sri Lanka, Thailand, Vietnam and Pakistan during 1985-2012. He found the effect of interest rate, M2, fiscal deficit, and government expenditure are statistically significant on inflation.

Honohan & Lane (2003) used multiple regression analysis to define annual inflation differentials across the Eurozone. The time period considered under the study is 1999-2001. The study shows that the variation in nominal effective exchange rate plays a crucial role in explaining inflation rates. Honohan & Lane (2004) in a related study endorse that exchange rate influences the European Union inflation rates during periods of Euro appreciation (2002–2003) and Euro depreciation (1999–2001).

Indian Studies on Inflation

The developing economies usually face the issue of fiscal deficit. There are many studies that focus on fiscal-based theories of inflation (Agraveli & Khan, 1978; Alesina & Drazen, 1991; Calvo & vegh, 1999). The oil price shocks also impact the inflation (Ghosh & Kanjilal, 2014). There is a long-term dependence between the oil price changes and CPI inflation (Se ket al., 2015). Mohanty & John (2015) used time-varying SVAR to identify the major determinants of inflation in India. They found that output gap had an uneven impact on inflation.

In India, there are a number of studies that deal with forecasting of inflation. A study by Mishra & Mishra (2010) demonstrates, how the volatility in inflation may be explained by the rising impact of exchange rate shocks. For this study, they considered the period between January 1996 and March 2005. The study tells about bigger and speedier impact of global supply shocks and external shocks. According to John (2003) exchange rates and money aggregates impacts the prices since 1991. The study by Patnaik (2010) demonstrates substantial impact of IIP on CPI. Kumar (2013) found a significant influence of money supply on prices for the period January 1992 to December 2012. Contrarily, Sabade (2014) did not find any direct relationship in prices and movements of money supply in the period 2010 to 2012.

The output gap is also able to predict the inflation dynamics in the short and medium terms (Tiwari et al., 2014). Mohanty & John (2015) employed time-varying SVAR model for identification of important determinants of inflation in Indian economy. The period under consideration was 1996-2014, and found that depreciation, money supply and negative output gap as leading explanatory of inflation.

Alam & Alam (2016) also considered the period of 1989-2013 for Indian economy and confirmed depreciation, money supply, and negative output gap as leading explanations of inflation. Gupta (1984) is one of the earliest studies on Indian inflation, inferred that both nominal and real income have a unidirectional cause on money supply. Nachane & Nadkarni (1985) found that money supply has a unidirectional causality to price and also is a major determinant of income. A large number of studies also explored the link between money supply, government deficit and inflation in India. Rangarajan & Mohanty (1998) confirmed that an important cause for inflation is government deficit. A contrarian view is reflected in the study by Ashra et al. (2004), who found no relationship between the inflation and fiscal deficit.

Mohanty (2010) discussed the rise in Indian inflation in 2008 and 2009, and noticed the supply side constrains. Tiwari & Tiwari (2011) examined the linkage between inflation and fiscal deficit in India. According to their study, inflation is not cause for fiscal deficit. Ashwani (2014) established the link between money supply, exchange rate, and private and social spending and inflation in both long as well as short term. Mohanty & John (2015) used time-varying SVAR model to identify the major determinants of inflation in India during the period 1996-2014. They confirmed the impact of monetary policy on inflation.

Data and Period of Study

The present study deploys monthly time series data of CPI from January 1960 to Dec 2018. The study also uses the data from January 2019 to January 2020 for validation of the ARIMA model. The data is being downloaded from open Federal Reserve Economic Data (https://fred.stlouisfed.org). The base year of this time series CPI data is 2015.

Results

The objective of this study is to create a forecasting model based on CPI, the chief indicator of inflation in India. Instead of considering the absolute value of CPI, log of monthly CPI value (LCPI) is being considered. The reason is that changes in the log of a variable denotes a relative change (or rate of return), whereas a change in the variable itself denotes an absolute change. This also implies that the returns are unit-free and that makes them more comparable (Gujarati, 2015). The total number of observations are N = 707.

Stationarity - Unit Root Test

First, the stationarity of the time series data is tested. For testing Stationarity, the Augmented Dicky-Fuller (ADF) test is being used. Following form is used for performing the test:

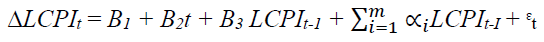(1)

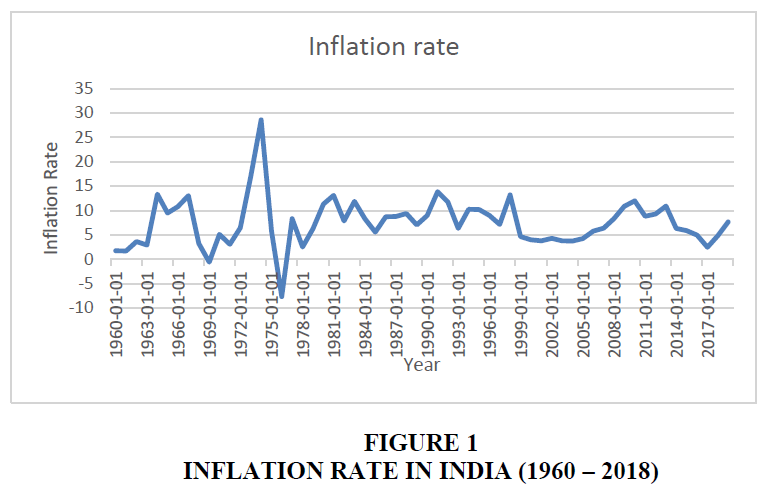
In every case, the null hypothesis is B₃ = 0 (i.e. unit root exists) and the alternative hypothesis is that B₃ <0 (i.e. no unit root). The result of the unit root test of LCPI with intercept is shown in Table 1 below. But, before that let’s have a look at the CPI curve starting from 1960 – 2018 (Figure 1).

Table 1 ADF test of LCPI with Level Difference
Null Hypothesis: LCPI has a unit root
Dependent Variable: D(LCPI)
Method: Least Squares
Sample (adjusted): 1961M02 2018M12
Included observations: 695 after adjustments
	t-Statistic	Prob.
Augmented Dickey-Fuller test statistic	-0.72051	0.8393
Test critical values:
1% level	-3.43953
5% level	-2.86548
10% level	-2.56893

To begin with, we select ‘level’ unit root test, in the Table 1 below,

In table 1, the DF critical values are -3.43953 (1% level), -2.86548 (5% level), and -2.56893 (10% level). The computed t value is -0.72051. In absolute terms, 0.72051 is smaller than any of DF critical values in absolute terms. Hence, we conclude that LCPI at level difference is not stationary.

Next, we will conduct the ADF test for 1^st difference of LCPI. The result is shown in Table 2 below:

Table 2 ADF test of LCPI with Level Difference
Null Hypothesis: D(LCPI) has a unit root
Dependent Variable: D(LCPI,2)
Method: Least Squares
Sample (adjusted): 1961M02 2018M12
Included observations: 695 after adjustments
	t-Statistic	Prob.
Augmented Dickey-Fuller test statistic	-4.656040	0.8393
Test critical values:
1% level	-3.971312
5% level	-3.416296
10% level	-3.130452

In Table 2, the DF critical values are -3.971312 (1% level), -3.416296 (5% level), and -3.130452 (10% level). The computed t value is -4.656040. In absolute terms, 4.656040 is bigger than any of DF critical values in absolute terms. Hence, we conclude that LCPI at first difference is stationary.

ARIMA Forecasting

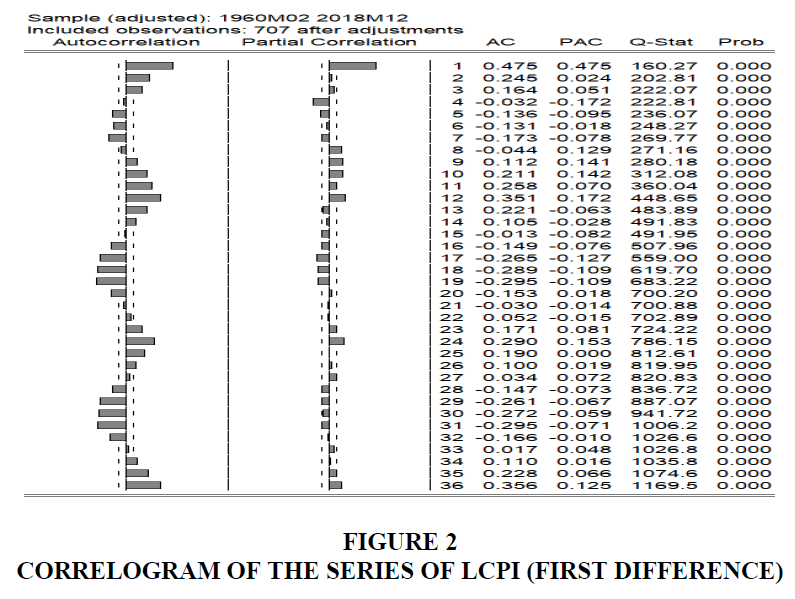
We obtained the correlogram of the time series ‘LCPI’, which is shown in Figure 2. It is observed that the auto-correlation function (ACF) of the series exhibits a dying out pattern of spikes. And there exists one significant spike for partial auto-correlation function (PACF) at lag1. These observations indicate that LCPI series is non-stationary. We have also seen that the application of unit root test further confirms this conclusion.

A careful examination of the correlogram shows that neither the ACF nor PACF shows the neat pattern described in table 2. To check the statistically significant correlations, note that the standard error of a (sample) correlation coefficient is given by √1/�� = √1/707 = 0.037609, where n is the sample size. Therefore, the 95% confidence interval for the true correlation coefficients is about 0 ± 1.96 (0.037609) = (-0.073713to 0.073713). Correlation coefficients lying outside these bounds are statistically significant at the 5% level. On this basis, it seems both ACF and PACF correlations at lags 1, and 5, seem to be statistically significant.

Since, we do not have the clear-cut pattern of the theoretical ACF and PACF outlined in Table 3, we can proceed by trial and error. First, let’s fit an autoregressive (AR) model at lags 1 and 5. The results are:

Table 3 Computation of AR (1) and AR (5)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.002595	0.000217	11.95496	0.0000
AR(1)	0.471316	0.026369	17.87408	0.0000
AR(5)	-0.120792	0.028964	-4.17047	0.0000
SIGMASQ	1.36E-05	5.53E-07	24.56058	0.0000
Akaike Info Criterion	-8.357544
Schwarz Criterion	-8.331739
Hannan-Quinn Criter.	-8.347574

Similarly, we may also compute the moving average (MA) models with lag 1 and lag 5 i.e. MA (1) and MA (5) as given in Table 4 below:

Table 4 Computation of MA (1) and MA (5)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.002598	0.000194	13.389	0.0000
MA(1)	0.438294	0.028393	15.43648	0.0000
MA(5)	-0.083253	0.028163	-2.95607	0.0032
SIGMASQ	1.42E-05	5.79E-07	24.58516	0.0000
Akaike Info Criterion	-8.309848
Schwarz Criterion	-8.284043
Hannan-Quinn Criter	-8.299877

Now, the question is, which model we should choose? Since the values of Akaike and Schwarz is lowest in the case of AR model, we can choose this over MA model. However, we may also try to develop a model using both AR and MA terms. The model considering AR (1), AR (5), MA (1) and MA (5) may be viewed in Table 5 below:

Table 5 Computation of AR (1), AR (5), MA (1) and MA (5)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.002595	0.000155	16.77964	0.0000
AR (1)	0.572562	0.006233	91.86376	0.0000
AR (5)	-0.572939	0.006168	-92.8842	0.0000
MA (1)	-0.466332	0.015928	-29.2778	0.0000
MA (5)	0.618386	0.017329	35.68406	0.0000
SIGMASQ	1.25E-05	5.02E-07	24.82338	0.0000
Akaike Info Criterion	-8.430875
Schwarz Criterion	-8.392167
Hannan-Quinn Criter	-8.415919

From table 5 above, AR (1), AR (5), MA (1), and MA (5) all are statistically significant. Therefore, we will try ARIMA (1,1,1), ARIMA (1,1,5), ARIMA (5,1,1) and ARIMA (5,1,5). First, we will try ARIMA (1,1,1). The results are shown in Table 6.

Table 6 ARIMA (1,1,1)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.002587	0.00028	9.235384	0.0000
AR (1)	0.522776	0.058772	8.895024	0.0000
MA (1)	-0.061444	0.068487	-0.89718	0.3699
SIGMASQ	1.38E-05	5.73E-07	24.15047	0.0000
Akaike Info Criterion	-8.339279
Schwarz Criterion	-8.313474
Hannan-Quinn Criter	-8.329309

As observed in table 6 above, the AR (1) is statistically significant but MA (1) is not significant. Therefore, ARIMA (1,1,1) model seems not very suitable. Next, we will try ARIMA (1,1,5). The results of ARIMA (1,1,5) is given below in Table 7.

Table 7 ARIMA (1,1,5)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.002594	0.000243	10.67574	0.0000
AR(1)	0.473207	0.026665	17.74608	0.0000
MA(5)	-0.095351	0.033268	-2.86617	0.0043
SIGMASQ	1.37E-05	5.60E-07	24.43843	0.0000
Akaike Info Criterion	-8.349469
Schwarz Criterion	-8.323664
Hannan-Quinn Criter	-8.339498

In ARIMA (1,1,5), both the AR (1) and MA (5) are statistically significant. Therefore, we may consider ARIMA (1,1,5) as valid. Next, we will try ARIMA (5,1,1). The results of ARIMA (5,1,1) is given below in Table 8. It is observed from Table 8 that both AR (5) and MA (1) is statistically significant.

Table 8 ARIMA (5,1,1)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.0026	0.000183	14.171	0.0000
AR (5)	-0.11867	0.032664	-3.63307	0.0003
MA (1)	0.433489	0.028706	15.10103	0.0000
SIGMASQ	1.42E-05	5.74E-07	24.72195	0.0000
Akaike Info Criterion	-8.312729
Schwarz Criterion	-8.286924
Hannan-Quinn Criter	-8.302758

The last model that we are going to test is ARIMA (5,1,5). The results of ARIMA (5,1,5) is shown in Table 9 below. It is observed that both AR (5) and MA (5) are significant.

Table 9 ARIMA (5,1,5)
Variable	Coefficient	Std. Error	t-Statistic	Prob.
C	0.0026	0.000141	18.42716	0.0000
AR(5)	-0.491208	0.158419	-3.10069	0.0020
MA(5)	0.335103	0.168584	1.987749	0.0472
SIGMASQ	1.73E-05	6.89E-07	25.14501	0.0000
Akaike Info Criterion	-8.114038
Schwarz Criterion	-8.088233
Hannan-Quinn Criter	-8.104067

Now, the question is, out of these three models i.e. ARIMA (1,1,5), ARIMA (5,1,1) and ARIMA (5,1,5), which one is most suitable. We may find the most suitable one by comparing Akaike Info Criterion (AIC) and Schwarz Info Criterion (SIC).

From the Akaike info criterion and Schwarz criterion, it may be observed that it’s minimum in case of ARIMA (1,1,5) model. It seems that the ARIMA (1,1,5) is the most appropriate model fit to depict the behavior of the level differences of the logs of monthly closing CPI over the sample period.

Finally, after considering the results of tests mentioned above, we choose ARIMA (1,1,5) as a suitable model for forecasting CPI. This model is used as an estimator for predicting future values of CPI. The principle of parsimony is taken into consideration, while selecting the model.

The generalized ARIMA (1,1,5) model may be written as (Chatfield, 2003):

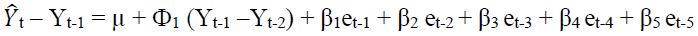(2)

Now, we may put the values of ARIMA (1,1,5) from table 7 into equation 2, where

μ = 0.002594

Ф1 = 0.473207

β1 = 0

β2 = 0

β3 = 0

β4 = 0

β5 = -0.095351

By putting the abovementioned values in equation 2, the model becomes,

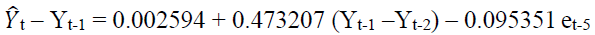(3)

Using this model, we compute the difference between the computed model value and the observed value for the sample data using equation 3. The root mean squared errors (RMSE) equals to 0.003701, which again recognized the suitability of model.

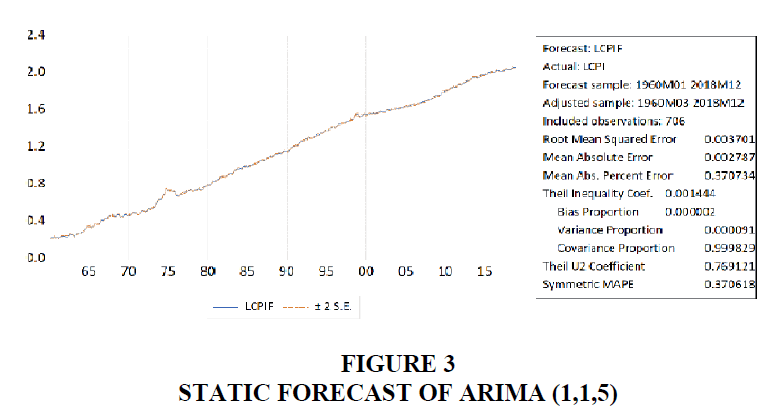
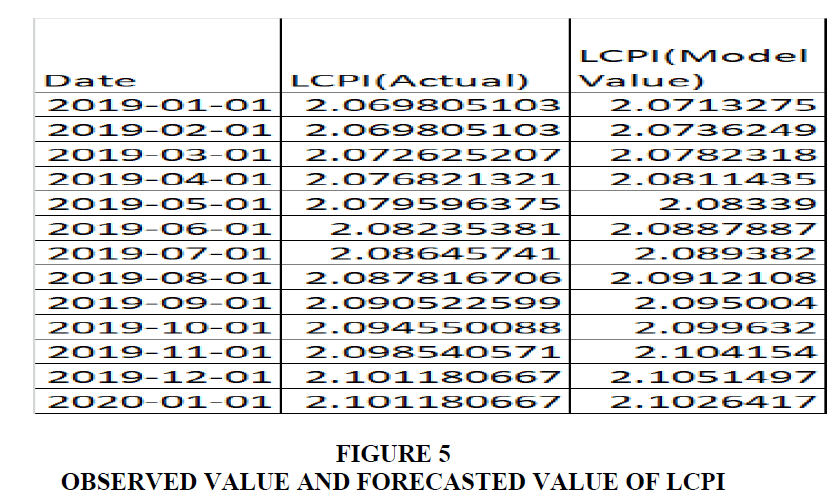
This ARIMA (1,1,5) model can be used for forecasting. The static forecast for the model is shown below Figure 3:

The accompanying table gives the same measures of the quality of the forecast, namely, the root mean square, mean absolute error, mean absolute percentage error, and the Theil Inequality Coefficient. For our model, the Theil Coefficient is almost zero, signifying that the fitted model is reasonably good.

Evaluation of Forecasts

The reliability of the forecasting model of LCPI may be gauged as per the following criterion:

1. The assessed coefficients of both AR (1) and MA (5) terms are statistically significant (table 7)

2. The value of Root Mean Squared Error (RMSE) for the estimated ARIMA (1,1,5) model is 0.003701 (Figure 3), which is pretty low. During the validation period also the RMSE is 0.004280567, which is on lower side.

3. The values of ‘bias proportion’, ‘variance proportion’, and ‘covariance proportion’ are 0.000002, 0.000091, and 0.999829 (figure 3) respectively. Since the values of bias and variance proportions are low, and that of covariance proportion is high, therefore the forecast may be considered satisfactory.

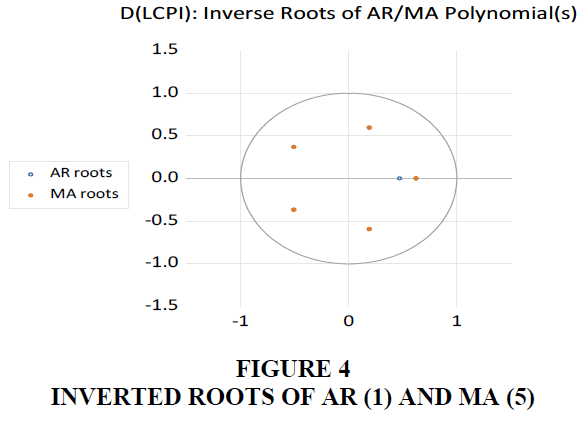
4. All inverted AR and MA roots are within the unit circle (Figure 4), which implies that the chosen ARIMA model is stationary and the model has been correctly specified.

For validation of the model, we again considered the monthly CPI data from January 2019 to January 2020. Figure 5 shows the beginning of month estimated value and the observed value of log of CPI by using equation 3. The RMSE for the period of validation is 0.004, which may be considered as pretty low and acceptable.

Discussions

Since the early 90s, developing countries across the world has started adopting inflation targeting (IT) strategy for economic control. IT is a monetary strategy adopted by central banks to maintain the level of inflation within a target range. In India, the RBI adopted the inflation targeting strategy since 2015. Their target to keep the inflation within 4%-6% range by 2021.

Applying the PESTLE model for analyzing the trend of inflation

The policymakers often use models for understanding the factors that may impact the inflation trend in the future. One of the popular model is PESTLE (political, economic, social, technological, legal, and environmental). PESTLE usually focuses on external conditions impacting the variable under consideration (Day, 1990; Walsh, 2005). The PESTLE model may be applied to understand the factors that impacts the trend of inflation in India.

One of the criticism of PESTLE model is that it is not considered to be originated in conceptual theory (Kourteli, 2000). However, over the years, this model is extensively used by decision makers for assessing the dynamic business and economic environment. In practice, PESTLE should demonstrate the connection of variables and the expected outcomes (Collins, 2010), for example, a change in exchange rate should impact the inflation rate.

Political Issues

Political issues have a major influence on inflation of a country and India is not an exception. It is evident from the literature that uncontrolled inflation often results into generating inefficiencies into economic system and social welfare. Over the years, India went through several political phases. Post-independence since 1947, the country adopted the democracy as a system. India is second largest parliamentary, secular democratic republic in the world. At one point of time, analysts were more concerned about political environment of a single country, and identifying the political decision-making concentrations (Simon, 1984; Thomas, 1974). The influence of political issues on economic matters started gaining momentum with liberalization of economic policies. India adopted liberal economic policies since early 90s. Till 90s the Indian economy was more oriented towards socialistic philosophies. The political changes have resulted into several economic reforms.

Economic reforms in India starting in 90s led to increased competition among the industrial sectors like banking, insurance, manufacturing and services. The inflation rate had also came down, as the economic reforms led to increased production resulting into lowering of prices. Economic reforms also led to increased competition, which also pushed the prices to come down.

Starting from 1960, India in general was governed by stable governments, barring a few brief periods. The country faced political instability during the periods 1977-80, 1989-91, and 1996-98. However, since 1998, though governments are run by coalition fronts, but they were able to complete the terms. For a stable economy and a stable inflation rate, a stable government is required. The economic reform process initiated in 1991 was pursued by successive governments in India. As a result, India witnessed unprecedented economic growth in the recent years. In fact, the Indian economy became one of the fastest economy in the recent years. At the turn of the century, the size of Indian economy was USD 480 billion, which has grown fivefold to reach USD 2.2 trillion in 2015. The future trend of inflation rate may depend on political stability of the country and the world as well.

Economic Factors

Prior to economic reforms in 1990s, the Indian economy was more leaned towards socialism. The process of economic reforms was initiated in early 1990s, and at that point of time the inflation rate was hovering around 16.7% (August 1991). An acute financial crisis drove the country to the door of IMF.

With the initiation of the reform process in 1990s, the economy became more competitive. With the end of license raj and entry of global players with a ready consumer market, the economic growth of the country jumped manifold. The country recorded a GDP growth of over 6 percent between 1991 and 2004, and over 8.5 percent between 2003 and 2007. It is the latter figure that has drawn the attention of the world when India became one of the fastest growing economies in the world after China (Mukherjee, 2009). With rising income and demand growth, the production needs also increased. Abolition of license raj enabled the companies to produce as much as possible without any government permissions.

The growth in Indian economy is continuing till now unabated. One challenge of rising economic growth is accompaniment of inflation. In a flourishing economy, keeping the inflation under control is always a challenging job. To meet this objective, the reserve bank of India started following the target inflation control system since 2015. The target is kept at 4% - 6% range. Though most of the time in recent history, the RBI being able to maintain the inflation rate within the targeted level, but in recent times the RBI is facing problem with controlling within the target level. The retail inflation in September 2020 has been spiked to 7.34%, which is way beyond the targeted limit of 6%. The reason for this could be the policy of quantitative easing followed by the central bank. This is not an Indian phenomenon alone, but followed by other central banks also across the globe.

Under the stressful COVID 19 scenarios, the global as well as the Indian economy is going through severe economic stress. The immediate challenge for the government is reviving the weakening economy. This may happen at the cost of rising inflation.

Social conditions

Social conditions, which encompass the social status, standard of living of citizens have important impact on national economy and inflation. In a developing nation like India, income disparity among social clusters create significant impact on economic variables. While India is one of the fastest growing economy in the world, at the same time, the country is also one of the most unequal country.

Rising inflation may have deep effect on income inequality. Rising inflation affects the lower income group people more severely compared to the higher income group. The high-income group usually invests in a portfolio of assets, whereas the low-income group primarily holds their assets in the form of cash. Inflation erodes the purchasing power of cash and severely impact the standard of living of poor. According to Oxfam, in the period between 2006 and 2015, ordinary workers saw their income rising by just 2% per year, whereas billionaire wealth rose at a rate six time faster.

Meanwhile, the unemployment rate has also increased in India. During the Covid era, the unemployment rate reached a peak of 23.5%. The relationship between inflation and unemployment can be defined by Philips curve. The Philips curve implies a trade-off between inflation and unemployment. As the unemployment increases the inflation decreases. In recent years, from the year 2008 to 2017 the unemployment rate decreased consistently from 4.12% to 3.51%. Unemployment Rate in India increased to 3.52 percent in 2017 from 3.51 percent in 2016. Unemployment Rate in India averaged up to 4.05 percent from 1983 until 2017, reaching an all-time high of 8.30 percent in 1983 and a record low of 3.41 percent in 2014.

Technological Developments

Technological developments affect inflation by improving the process of production and supply chain. Improved technology enhances the efficiency, and reduces the cost. Automation facilitates replacement of labour in the process of production and reduces cost. Autor et al. (2006) has found a strong connection between the fall of the share of labor income and the rise of large firms in the U.S. As wealthy peoples’ marginal propensity to consume is lower, worsening income distribution may continue to drag down aggregate demand and may curb rising inflation. The Indian industry has seen unprecedented rise in spending on automation in recent years. This happened in line with the global developments. The penetration of internet has also increased during the recent years. The competition among the producers has also increased to reach the customers. This also resulted into lower price.

With emergence of 5G communication systems in the country, and improved data communications, there is increasing possibility that the industrial productivity performance will only grow with time.

Legal considerations

The economic environment of a country is usually regulated by government and regulatory authorities. In India, the economic environment of the country is continuously monitored and regulated by several self-regulating institutions, policy making bodies and government ministries. The major regulatory bodies and their primary area of influence is given in the Table 10 below:

Table 10 Regulatory Authorities in India
Sl. No.	Institution	Area of Influence
1.	Securities and Exchange Board of India	Capital Market
2.	Insurance Regulatory and Development Authority of India	Insurance
3.	Reserve Bank of India	Money and Banking
4	Pension Fund Regulatory and Development Authority of India	Pensions
5.	Ministry of Finance, Government of India	Economy of India

Environmental Aspects

The economic environment of the country plays an important role in shaping the inflation figures. Post the economic liberalization in the country, the competitiveness among the business entities increased significantly. In the year 2019, the global ranking of ‘ease of doing business’ (EODB) has increased to 63^rd position globally from the 77^th position in 2018, 100^th position in 2017 and 130^th position in 2016. This development indicates towards the overall growth of Indian economy.

The government of India has undertaken several initiatives to improve the economic environment of the country. The 2020 World Bank report is showing the current position of EODB of various countries in Table 11.

Table 11 World Bank ease of doing Business Ranking 2020
Country	Rank
New Zealand	86.8
Singapore	86.2
Denmark	85.3
Korea	84
United States	84
United Kingdom	83.5
Canada	79.6
China	77.9
France	76.8
India	71

Conclusion and Future Scope of Research

Inflation is a major area of interest for study as it impacts the life of common people directly. It influences the standard of living, gross demand generation in the economy. Forecasting of inflation is therefore an important issue to ponder upon. Economists are interested about it, because a nearly accurate forecasting may be of great help in formulation economic policies of a country.

In this paper, we considered consumer price index (CPI) of India as a proxy for measuring inflation. We formulated an ARIMA (1,1,5) model, that may be used in forecasting CPI. We found the model parameters are showing satisfactory results. One of the limitations of this paper is that we used only CPI as measure of inflation. In future, this study may be further extended by including the other measures of inflation e.g. wholesale price index (WPI). A study of inflation on individual components of CPI may also be undertaken.

Acknowledgement

We acknowledge the support of Dr. Gautam Bandyopadhyay, Associate Professor. National Institute of Technology, Durgapur. India in writing this paper.

References

1. Agraveli, B.B., & Khan, M. (1978) Government deficits and the inflationary process in developing countries. IMF Staff Papers, 25(3), 383
2. Alam, M.Q., & Alam, M.S. (2016). The Determinants of Inflation in India: The Bounds Test Analysis. International Journal of Economics and Financial Issues, 6(2), 544-550.
3. Alesina, A., & Drazen, A. (1991). Why are stabilizations delayed? American Economic Review, 81(5), 1170-1188.
4. Ashra, S., Chattopadhyay, S., & Chaudhuri, K. (2004). Deficit, money, and price: The Indian experience. Journal of Policy Modeling, 26(3), 289-299.
5. Ashwani, D. (2014) Determinants of inflation in India: A cointegration approach. International Journal of Multidisciplinary Consortium, 1(1),1-11.
6. Autor, D., Katz, L., & Kearney, M. (2006). The polarization of the U.S. labour market, American Economic Review, 96(2), 189-194.
7. Calvo, G.A., & Vegh, C.A. (1999). Inflation stabilization and bop crisis in developing countries. Handbook of Macroeconomics (pp. 1531-1614). Amsterdam, North Holland: Elsevier.
8. Collins, R. (2010). A graphical method for exploring the business environment. Henley-on-Thames, England: Henley Business School.
9. Day, G.S. (1990). Market driven strategy: Processes for creating value. New York, NY: The Free Press.
10. Enke, D., & Mehdiyev, N. (2014). A hybrid neuro-fuzzy model to forecast inflation. Precedia Computer Science, 36, 254-260.
11. Ghosh, S., & Kanjilal, K. (2014). Oil price shocks on Indian economy: Evidence from Toda Yamamoto and Markov regime-switching VAR. Macroeconomics and Finance in Emerging Market Economics, 7(1), 122-139.
12. Gujarati, D. (2015). Econometrics by Example. Palgrave. 302-306.
13. Gupta, G.S. (1984). Monetary target setting. Ahmedabad, India: Indian Institute of Management.
14. Honohan, P., & Lane, P.R. (2003). Divergent inflation rates in EMU. Economic Policy, 37, 359-394.
15. Hurtado, C., Luis, J., Fregoso, C., & Hector, J. (2013). Forecasting Mexican inflation using neural networks. International Conference on Electronics, Communications, and Computing, 32-33.
16. John, R.M. (2003). Inflation in India: An Analysis Using Post-Liberalisation Data. Available at SSRN: https://ssrn.com/abstract=470465 or http://dx.doi.org/10.2139/ssrn.470465.
17. Kharimah, F., Usman, M., Elfaki, W., & Elfaki, F.A.M. (2015). Time series modelling and forecasting of the consumer price Bandar lampung. Science International, 27(5),4119-4624.
18. Kock, A.B., & Terasvirta, T. (2013). Forecasting the Finnish consumer price inflation using artificial network models and three automated model section techniques, Finnish Economic Papers, 26(1), 13-24.
19. Kourteli, L. (2000). Scanning the business environment: Some conceptual issues. Benchmarking: An International Journal, 7(5), 406-413.
20. Kumar, R. (2013). A study of inflation dynamics in India: A cointegrated autoregressive approach, IOSR Journal of Humanities and Social Sciences, 8(1), 65-72.
21. Manga, G.S. (1977) Mathematics and statistics for economics, Vikas Publishing House, New Delhi. India.
22. Mcnelis, P.D., & Mcadam, P. (2004). Forecasting inflation with think models and neural networks, Working paper series. (accessed at https://www.econstor.eu/bitstream/10419/152786/1/ecbwp0352.pdf).
23. Meyler, A., Kenney, G., & Quinn, T. (1998). Forecasting Irish inflation using ARIMA models, Research and Publication Departmen, Central Bank of Ireland.
24. Milo, P. (2012), The impact of the budget deficit on the currency and inflation in the transition economics. Journal of Central Banking Theory and Practice, 1(1),25-57.
25. Mishra, A., & Mishra, V. (2010). A VAR model of monetary policy and hypothetical case of inflation targeting in India, Discussion paper 15/10, Monash University.
26. Mohanty, D. (2010). Measures of Inflation in India: Issues and Perspectives. In IARNIW Conference Speech, Thiruvananthapuram.
27. Mohanty, D., & John, J. (2015). Determinants of inflation in India. Journal of Asian Economics, 36(C),86-96.
28. Nachane, D.M., & Nadkarni, R.M. (1985). Empirical tests of certain monetarist propositions via causality theory. Indian Economic Journal, 33, 139-155.
29. Nguyen, V.B. (2015). Effects of fiscal deficit and money M2 supply on inflation: Evidence from selected economies of Asia. Journal of Economics, Finance and Administrative Science, 20(38),49-53.
30. Owusu, F.K. (2010). Time series ARIMA modelling of inflation in Ghana: (1990 – 2009). http://hdl.handle.net/123456789/866
31. Patnaik, A. (2010). Study of inflation in India: a cointegrated vector autoregressive approach. Journal of Quantitative Economics, 8(1) 118-129.
32. Rangarajan, C., & Mohanty, M.S. (1998). Fiscal deficit, external balance and monetary growth. RBI Occasional Papers, 18, 635-653.
33. Sabade, S. (2014). Is money supply the cause of inflation in India? An alternative postulate to understand inflation. Precedia Social and Behavioral Sciences, 133, 379-382.
34. Simon, J.D. (1984). A theoretical perspective on political risk. Journal of International Business Studies, 15(3), 123-143.
35. Subhani, M.I., & Panjwani, K. (2009). Relationship between consumer price index (CPI) and government bonds, South Asian Journal of Management Sciences, 3(1), 11-179.
36. Thomas, P.S. (1974). Environmental analysis for corporate planning. Business Horizons, 17(5), 27-38.
37. Tiwari, A.K., Oros, C., & Albulescy, C.T. (2014). Revisiting the inflation-output gap relationship for France using a wavelet transform approach. Economic Modelling, 37, 464-475.
38. Tiwari, A.K., & Tiwari, A.P. (2011). Fiscal deficit and inflation: An empirical analysis for India. The Romanian Economic Journal, 14(2),131-158.
39. Walsh, P.R. (2005). Dealing with the uncertainties of environmental change by adding scenario planning to the strategy reformation equation. Management Decision, 43(1), 113-122.