Journal of Economics and Economic Education Research (Print ISSN: 1533-3590; Online ISSN: 1533-3604)

Research Article: 2019 Vol: 20 Issue: 2

How Early Should We Worry? Weekly Classroom Predictors of Academic Success and University Retention in an Introductory Microeconomics Course

Matthew Kutch, Ohio Northern University

Abstract

With increasing financial pressure on higher education, concern for student retention is growing. Most previous work on retention focused on factors unobservable to a faculty member, including measures of social, academic, and financial support. This study uses weekly data on attendance, low-impact high-frequency assignments, and high-impact low-frequency exam performance to model course performance and retention. The models confirm the value of an early warning system for course performance (e.g., midterm grades) after the first high impact exam. The models suggest potential value in adding an end-of-semester warning system for retention based on performance on low-impact high frequency assignments.

Keywords

Student Retention, Finance of Higher Education, Weekly Attendance & Assignments

Introduction

With increasing pressures on the finances of higher education, retention is an increasing concern (Hoover, 2016). For universities, low rates of retention translate into potentially significant lost future revenue. For the broader society, low rates of retention mean inefficient allocations of public funds and potential negative implications for future labor markets (O'Keeffe, 2013). For students, failure to persist represents a loss of foregone future income and possibly psychological well-being (Mangum et al., 2005).

Much of the previous work on retention focuses on integrating students into the university environment and providing academic, social, and financial support to support goal commitment. Much of the previous work on retention relies on final course grades and semester GPA as the source of information on academic performance.

While faculty teaching a course may only observe a small slice of these a student’s overall “university experience”, they often collect a continual flow information throughout the semester related to classroom performance and behavior. I am not aware of any previous work that attempts to use information collected during a semester to explain student retention as this work will.

Given the large amount of attention on freshman retention over the last two decades, the problem of sophomore retention (aka, “fifth semester retention”) may become increasingly important as first-year retention improves.

The following study is organized around the following two questions. Can observable classroom data from sophomore-level principles of microeconomics course help identify overall course performance and future retention? How early in the semester do the classroom behaviors begin to relate to overall course performance and future retention? Knowing how early the classroom behaviors reflect final course performance and future retention may inform the appropriate timing of early warning systems (i.e., midterm grade reports).

While these conclusions are specific to Ohio Northern University, a small, private Midwestern university, the method is quite general and could be applied to other classrooms and universities with minimal data requirements.

Literature Review

Two early significant works of student retention are Tinto’s (1987) student integration model of retention and Astin’s (1985) student involvement theory focus on the impact of student intent and interdependence with the academic and social environment on retention. More recent works incorporate external forces into models of retention. For a good review of attempts to integrate the major theoretical models of student retention, (Sauer & O’Donnell, 2006). Wetzel et al. (1999) evaluated Tinto’s integration model of retention, finding academic and social integration most significant in predicting student retention.

This study attempts to model information only on student performance and behaviors in the classroom readily available and apparent to a faculty member.

A number of studies examined the role of both internal and external factors on student retention. Gerdes & Mallinckrodt (1994) considered the association between a pre-enrollment survey assessment of attitudes of emotional and social adjustment and subsequent dropping out, finding emotional and social adjustment issues better predictors of than academic adjustment items. Longden (2006) provided a discussion of potential barriers to retention, highlighting the interplay of institutional response and student expectations of university services and culture. Morganson et al. (2015) explored the use of an embeddedness framework (fit, link, and sacrifice) for understanding and increasing retention in STEM students. Angulo-Ruiz & Pergelova (2013) found institutional image was significant for retention through the use structural equation modeling. Langbein & Snider (1999) connected course evaluations to university retention, finding a nonlinear, concave down relationship between the variables.

Much of the retention literature focuses on the role of first year courses. Tompson & Brownless (2013) described the purposeful design and implementation of a first year course to enhance business student retention. Critical to the design on the first year course was early and frequent interaction with faculty, staff, and peers, clearly communicated academic expectations and requirements, learning opportunities to increase involvement with other students, and academic, social, and personal support. Cox et al. (2005) described a thoughtful, purposefully-designed first year experience course and the positive impact on both GPA and persistence of business students.

Braunstein et al. (2005) focused on the impact of a freshman business course on the first year retention, exploring the impact of 9/11 in mitigating gains from a freshman business course on freshman attrition.

Bain et al. (2013) considered the impact of active learning techniques in a freshman-level business course to promote commitment and motivation through discipline and career awareness, finding positive results for an active class environment against a control class.

Bennett & Kane (2010) also focused on first year undergraduate retention. They focus on institutional organization and management practices of English universities with a focus on lowest rates of first year business student retention. Universities with high quality teaching and learning experiences in the organization’s culture, open communication, and openness to educational initiatives were associated with high first year business student retention.

An additional strategy for improving retention in the literature relates to recruiting efforts. Schertzer et al. (2004) emphasized enrolling students with strong value congruence with the university and faculty to improve retention. Rudd et al. (2014) argued for adding more rigorous recruiting techniques to maximize future retention in addition to the more traditional recommendations of academic, social, and financial support.

Improving academic advising and other support system is another strategy to boost retention identified in the literature. McChlery & Wilkie (2009) argued for examining different types of student support systems, including pastoral support, to enhance retention of at-risk students. They found an evaluation of pastoral support incurred a significant resource expense without a significant impact on retention. Kim & Feldman (2011) examined the role of academic advising in improving retention arguing for the importance of clear matching of the need for and expectations of academic advising. Pearson (2012) argued for the use of counseling-trained mentors in improving retention in graduate education. Thompson & Prieto (2013) considered the role of virtual advising as a potential substitute for face-to-face advising to produce satisfaction and motivation to matriculate.

Blake & Mangiameli (2012) advocated using data mining techniques to improve models to predict retention, ideally focusing on demographics, financial aid, background family education, performance, standardized tests, and faculty experience. Their work focused the role of a unique, required business student engagement program beginning in the freshman year and in helping to identify potential retention risks.

Description of the Data and Variables

The data were taken from 10 sections of sophomore-level principles of microeconomics course taught from 2013 to 2015, including both fall and spring semesters, at a small, private Midwestern University. Data were extracted from course records in a learning management system.

The data included two dependent variables of academic performance: course grade (on a 100 point scale) and dropping out. Course Grade is the end-of-semester numerical course grade on a traditional 100-point scale. It was typically calculated as 15-20% Assignments, 15-20% Exams, 20-25% Term Paper, and 20-25% Final Exam. Drop Out was a binary variable that identifies if student left the university any semester from fall 2013 to fall 2016.

The data also included three types of independent variables that most closely resemble knowledge, in-class engagement, and out-of-class engagement. Exam 1 and Exam 2 measured scores of high-impact, infrequent exams, spaced at roughly equal points of the semester. Assignments measured scores of low-impact, high frequency assignments (weekly or biweekly). The Assignments variable was presented as both a weekly score and a cumulative score. Attendance measured with days missed per week on a typical three-day a week semester schedule. Attendance in a two-day a week semester schedule was scaled to a three-day a week equivalent. Attendance was not used an explicit factor in the end-of-semester course grade calculation. The Attendance variable was measured as a cumulative total throughout the semester.

The goal of this work was to find a small model based on observable variables of classroom behavior and performance with some predictive power. While past literature suggests a wide range of variables related to retention, almost none are typically observed in the classroom or available to faculty (family SES, High School GPA, etc.). The goal of this study was to identify variables most observable to a faculty member to give them guidance on when to act on that information.

Basic Statistics

Table 1 presents basic statistics on the variables for the full sample. Students earning final grades of A-C are compared to student earning final grades of C-F. The data confirms prior expectations of the relationships; higher performing students are less likely to drop out, have fewer days missed, and have higher scores on weekly assignments. Interesting, the attendance between the groups is not statistically different for the first few weeks of the semester leading up to the first exam.

Table 1: Principles of Microeconomics Student Performance and Behavior (2013-2015) by Final Grade
  Overall (n=285) ABC (n=248) CDF (n=37)  
  Mean St Dev Mean St Dev Mean St Dev Significance
Course grade 0.793 0.113 0.824 0.063 0.588 0.152 <0.001
Drop out 0.060 0.237 0.020 0.141 0.324 0.475 <0.001
Exam 1 0.772 0.105 0.787 0.094 0.672 0.120 <0.001
Exam 2 0.731 0.116 0.749 0.097 0.606 0.157 <0.001
Attendance (days missed)
Week 1 0.02 0.16 0.03 0.17 0.00 0.00 0.001
Week 2 0.10 0.38 0.09 0.36 0.19 0.52 0.261
Week 3 0.23 0.57 0.21 0.55 0.41 0.72 0.115
Week 4 0.35 0.77 0.30 0.73 0.66 0.96 0.035
Week 5 0.48 0.96 0.39 0.83 1.07 1.45 0.009
Week 6 0.72 1.22 0.59 1.03 1.57 1.90 0.004
Week 7 0.99 1.60 0.83 1.35 2.04 2.53 0.007
Week 8 1.15 1.87 0.96 1.52 2.45 3.14 0.007
Week 9 1.36 2.25 1.11 1.78 3.03 3.85 0.005
Week 10 1.57 2.53 1.27 2.02 3.57 4.24 0.003
Week 11 1.80 2.95 1.43 2.31 4.30 4.97 0.001
Week 12 2.19 3.50 1.76 2.75 5.14 5.88 0.001
Week 13 2.43 3.92 1.90 2.96 5.95 6.84 0.001
Assignments (weekly)
Week 2 0.866 0.160 0.886 0.128 0.725 0.257 0.001
Week 4 0.860 0.199 0.877 0.176 0.744 0.291 0.010
Week 6 0.856 0.202 0.890 0.149 0.627 0.326 <0.001
Week 8 0.854 0.233 0.892 0.165 0.596 0.405 <0.001
Week 10 0.855 0.201 0.883 0.151 0.668 0.346 0.001
Week 12 0.847 0.265 0.901 0.184 0.485 0.407 <0.001
Assignments (cumulative)
Week 2 0.866 0.160 0.886 0.128 0.725 0.257 0.001
Week 4 0.863 0.151 0.882 0.127 0.735 0.219 <0.001
Week 6 0.860 0.147 0.885 0.118 0.699 0.208 <0.001
Week 8 0.859 0.142 0.886 0.103 0.673 0.215 <0.001
Week 10 0.858 0.137 0.886 0.095 0.672 0.211 <0.001
Week 12 0.856 0.140 0.888 0.089 0.641 0.211 <0.001

Table 2 presents basic statistics on the variables for the full sample and compares students who persist to those who drop out. The data confirms prior expectations of the relationships; students who persist have higher course grades, less days of class missed, and higher scores on weekly assignments. Interesting, the attendance between the groups is not statistically different for the first few weeks of the semester leading up to the first exam.

Table 2: Principles of Microeconomics Student Performance and Behavior (2013-2015) by Drop Out Status
  Overall (n=285) Persisted (n=268) Dropped out (n=17)  
  Mean St Dev Mean St Dev Mean St Dev Significance
Course grade 0.793 0.113 0.808 0.083 0.558 0.220 <0.001
Exam 1 0.772 0.105 0.776 0.100 0.706 0.151 0.076
Exam 2 0.731 0.116 0.739 0.104 0.609 0.212 0.023
Attendance (days missed)
Week 1 0.02 0.16 0.03 0.16 0.00 0.00 0.008
Week 2 0.10 0.38 0.09 0.35 0.35 0.70 0.139
Week 3 0.23 0.57 0.21 0.55 0.53 0.87 0.159
Week 4 0.35 0.77 0.32 0.74 0.82 1.07 0.075
Week 5 0.48 0.96 0.43 0.87 1.32 1.69 0.044
Week 6 0.72 1.22 0.63 1.08 2.12 2.20 0.014
Week 7 0.99 1.60 0.88 1.40 2.82 3.04 0.018
Week 8 1.15 1.87 1.00 1.59 3.50 3.74 0.015
Week 9 1.36 2.25 1.17 1.86 4.44 4.63 0.010
Week 10 1.57 2.53 1.34 2.12 5.18 4.93 0.006
Week 11 1.80 2.95 1.52 2.46 6.21 5.66 0.004
Week 12 2.19 3.50 1.86 2.91 7.41 6.76 0.004
Week 13 2.43 3.92 2.02 3.17 8.79 7.76 0.002
Assignments (weekly)
Week 2 0.866 0.160 0.871 0.153 0.775 0.232 0.109
Week 4 0.860 0.199 0.868 0.189 0.734 0.298 0.084
Week 6 0.856 0.202 0.870 0.182 0.640 0.338 0.013
Week 8 0.854 0.233 0.872 0.202 0.556 0.431 0.008
Week 10 0.855 0.201 0.866 0.182 0.677 0.356 0.044
Week 12 0.847 0.265 0.880 0.214 0.327 0.411 <0.001
Assignments (cumulative)
Week 2 0.866 0.160 0.871 0.153 0.775 0.232 0.109
Week 4 0.863 0.151 0.870 0.145 0.754 0.201 0.033
Week 6 0.860 0.147 0.870 0.136 0.716 0.220 0.011
Week 8 0.859 0.142 0.870 0.124 0.676 0.254 0.006
Week 10 0.858 0.137 0.869 0.117 0.676 0.253 0.006
Week 12 0.856 0.140 0.871 0.114 0.618 0.258 0.001

Methodology

Models of Academic Success

In order to analyze classroom performance and the subsequent probability of dropping out, this study proceeds with estimation of the following models. The first considers final course grade as a simple linear function of the observable classroom characteristics (X- attendance, assignments and exams). This model is estimated at the end of the semester conditional on the information available before the final exam and for each week throughout the semester conditional on the information available up to that point. The model is expected to have negligible predictive power after the first week of the semester with increasing predictive power as the semester progresses.

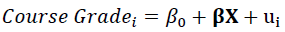
image

The second models the probability of a student dropping out according to a probit model using the same observable classroom characteristics (X-attendance, assignments and exams). This model is estimated at the end of the semester conditional on the information available before the final exam and for each week conditional on the information available up to that point in the semester. This model also is expected to have negligible predictive power after the first week with increasing predictive power as the semester progresses.

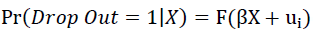
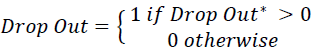
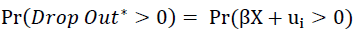
image

image

image

Where, F () is the cumulative distribution function of the error.

Results

Results of Course Performance Models

Table 3 presents estimation of the basic model to explain overall course grade. Not surprisingly, all variables are statistically significant with expected signs. In an attendance only model, increasing the number of days missed in the semester is associated with a 1.41% decrease in overall course grade. In the full model, increasing the number of days missed in the semester is associated with a 0.60% decrease in overall course grade.

Table 3: Course Grade Regression Models
  Attendance Week 12 (Days Missed) Exam 1 Exam 2 Assignments Week 12 (cumulative) Constant R2 Adj. R2
Model 1 -0.014***
(0.002)		       0.827***
(0.007)		 0.241 0.238
Model 2   0.670***
(0..050)		     0.276***
(0.039)		 0.387 0.385
Model 3     0.711***
(0.039)		   0.274***
(0.029)		 0.539 0.537
Model 4       0.598***
(0.032)		 0.281***
(0.028)		 0.548 0.546
Model 5 -0.006***
(0.001)		 0.330***
(0.036)		 0.297***
(0.034)		 0.337***
(0.026)		 0.048***
(0.026)		 0.818 0.814

Increased performance on exams 1 & 2, and weekly assignments are associated with an increase in the overall course grade. This is not surprising, given the role exams and weekly assignments play in the calculation of course grade1. The full model, as small as it is, has an R2 of 0.8182. This represents the model using the information available in the closing days of the semester but prior to the final exam.

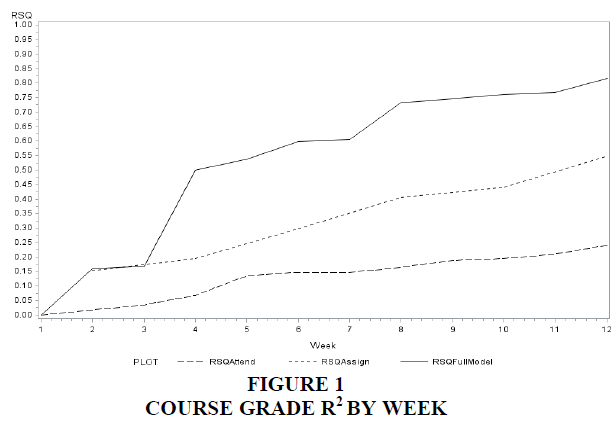
Table 4 presents week-by-week regression of overall course grade as a function of the information available up to that point in the semester. In the first week of the semester, with only attendance from the start of the semester, almost no information on classroom behavior is useful in predicting the overall course performance (R2 of <0.001 with a statistically insignificant model). Often these opening days of the semester include “syllabus days” and students rearranging their schedules. In the final week of the semester, attendance, assignments, and exams explain nearly 81% of the variation in end-of-semester course grade.

Table 4: Principles of Microeconomics Course Grade Regression by Week
  Attendance (days Missed) Assignments (Cumulative) Exam 1 Exam 2 Constant R2 Adj. R2
Week 1 0.015
(0.043)		       0.793***
(0.007)		 0.000 -0.003
Week 2 -0.024
(0.016)		 0.269***
(0.039)		     0.563***
(0.035)		 0.160 0.154
Week 3 -0.025**
(0.011)		 0.262***
(0.039)		     0.572***
(0.035)		 0.169 0.163
Week 4 -0.027***
(0.006)		 0.191***
(0.034)		 0.588***
(0.047)		   0.185***
(0.041)		 0.499 0.494
Week 5 -0.033***
(0.005)		 0.157***
(0.033)		 0.594***
(0.045)		   0.215***
(0.040)		 0.537 0.533
Week 6 -0.025***
(0.004)		 0.239***
(0.032)		 0.567***
(0.043)		   0.169***
(0.037)		 0.599 0.595
Week 7 -0.020***
(0.003)		 0.239***
(0.032)		 0.57***
(0.042)		   0.168***
(0.037)		 0.606 0.602
Week 8 -0.013***
(0.002)		 0.237***
(0.029)		 0.316***
(0.043)		 0.365***
(0.041)		 0.094***
(0.031)		 0.734 0.730
Week 9 -0.012***
(0.002)		 0.228***
(0.028)		 0.328***
(0.042)		 0.355***
(0.040)		 0.102***
(0.030)		 0.747 0.743
Week 10 -0.01***
(0.001)		 0.272***
(0.029)		 0.329***
(0.041)		 0.332***
(0.039)		 0.079***
(0.030)		 0.762 0.758
Week 11 -0.009***
(0.001)		 0.265***
(0.029)		 0.333***
(0.040)		 0.330***
(0.039)		 0.085***
(0.030)		 0.767 0.764
Week 12 -0.006***
(0.001)		 0.337***
(0.026)		 0.330***
(0.036)		 0.297***
(0.034)		 0.048*
(0.026)		 0.816 0.814

To help visualize the week-by-week gain in the predictive power of the model, Figure 1 shows the weekly progression of the R2 of the overall course model. As would be expected, the greatest increase in the predictive power of the model comes after the first high-impact knowledge-based exam. Figure 1 also shows the R2 of an attendance-only model and an assignments-only model.

economic-education-research-course-grade

Figure 1. Course Grade R2 by Week

Results of Dropping out Models

Table 5 presents estimation of the basic model to explain dropping out. In the combined model, only attendance and weekly assignments are statistically significant with expected signs. Increasing the number of days missed in the semester (evaluated at the means) is associated with a 0.0043 increase in the probability of dropping out (0.0263 to 0.0306).

Table 5: Drop Out Probit Models
  Attendance Days Missed (Week 12) Exam 1 Exam 2 Assignments Constant R2 Rescaled R2
Model 1 0.126***
(0.026)		       -2.01***
(0.171)		 0.079 0.218
Model 2   -2.662**
(1.093)		     0.436
(0.812)		 0.022 0.059
Model 3     -3.545***
(1.003)		   0.905
(0.690)		 0.05 0.138
Model 4       -2.161***
(0.349)		 -0.048
(0.259)		 0.132 0.362
Model 5 0.066**
(0.036)		   -2.17
(1.362)		 -1.637***
(0.399)		 0.95
(1.001)		 0.151 0.415

Increased performance on the final weekly assignment is associated with decrease in the probability of dropping out. Stated differently, failure to complete the final weekly assignment is associated with a 0.2924 increase in the probability of dropping out (0.0263 to 0.3187). Interestingly, while the cumulative weekly assignment total score was most useful in the course performance model, the week-by-week assignment score is most useful in the dropping out model.

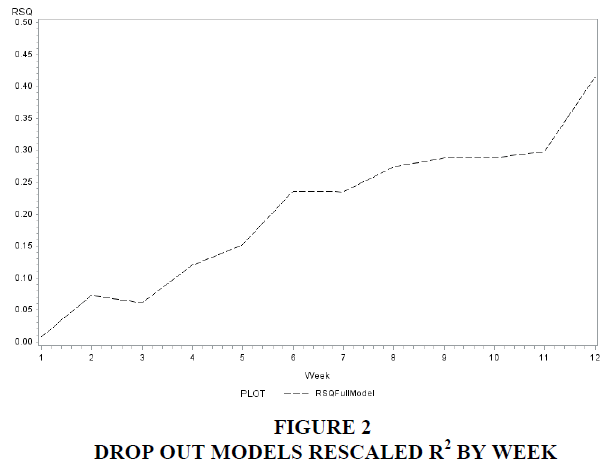
Table 6 presents week-by-week probit models of dropping out as a function of the information available up to that point in the semester. Again, in the first week of the semester, with only attendance from the start of the semester, almost no information on classroom behavior is useful in predicting dropping out. The predictive power of the model increasing throughout the semester with the largest gain in the predictive power of the model comes in the final week of the semester.

Table 6: Drop Out Probit Regression by Week
  Attendance Days Missed Assignments (Cumulative) Exams  (Cumulative) Constant R2 Rescaled R2
Week 1 -3.697
(247.2)		     -1.545***
(0.119)		 0.003 0.008
Week 2 0.441**
(0.225)		 -1.07*
(0.575)		   -0.734
(0.498)		 0.027 0.073
Week 3 0.265
(0.171)		 -1.045*
(0.577)		   -0.765
(0.507)		 0.022 0.061
Week 4 0.255**
(0.127)		 -0.668
(0.508)		 -2.321**
(1.149)		 0.598
(0.869)		 0.044 0.12
Week 5 0.277***
(0.103)		 -0.468
(0.524)		 -2.453**
(1.160)		 0.456
(0.881)		 0.055 0.152
Week 6 0.257***
(0.086)		 -0.974*
(0.505)		 -2.368*
(1.212)		 0.693
(0.911)		 0.086 0.236
Week 7 0.193***
(0.064)		 -1.000**
(0.504)		 -2.438**
(1.213)		 0.765
(0.907)		 0.086 0.235
Week 8 0.157***
(0.056)		 -0.812*
(0.472)		 -2.865**
(1.329)		 0.863
(0.914)		 0.1 0.274
Week 9 0.144***
(0.047)		 -0.752
(0.478)		 -2.871**
(1.336)		 0.793
(0.915)		 0.105 0.288
Week 10 0.148***
(0.039)		 -0.661
(0.536)		 -3.103**
(1.322)		 0.847
(0.985)		 0.105 0.288
Week 11 0.132***
(0.033)		 -0.594
(0.549)		 -3.1226**
(1.339)		 0.791
(1.000)		 0.108 0.298
Week 12 0.066**
(0.035)		 -1.637***
(0.399)		 -2.170
(1.362)		 0.950
(1.001)		 0.151 0.415

Figure 2 highlights the importance of this final weekly assignment in increasing the predictive power of the model. The largest gain in the predictive power of the model is not from information on the first exam; rather, it is performance on the final weekly assignment. This is quite remarkable, given the very small impact this assignment would have on overall course grade. This finding fits with the Luthans et al. (2012) model of critically diminished psychological capital (PsyCap), with the critical loss of psychological resources at the end of the semester.

economic-education-research-models-rescaled

Figure 2. Drop Out Models Rescaled R2 by Week

Discussion

Of the 21 students who did not complete a final assignment for the semester, none of them fell a letter grade because of it. To further emphasize the importance of that final assignment in predicting dropping out, a model with the final course grade has a rescaled R2 of 0.419. This contrasts with a model of attendance, assignments, and the exams right before the final exam having a rescaled R2 of 0.415. This seems to suggest waiting until final semester grades are posted adds very little value, especially given the decrease in face-to-face opportunities for intervention. Another way to emphasize the importance of this final assignment, a dropping out model that only includes only whether or not the student completed the final assignment had a rescaled R2 of 0.319. A model of dropping out that only includes the penultimate assignment only had a rescaled R2 of 0.057; the significant gain in the predictive power of the model is not from looking at their overall weekly assignment performance, rather it is by focusing on the last assignment for the semester. While this assignment has a negligible impact on course letter grade, it contains a tremendous amount of predictive information on dropping out.

A statistical limitation of this study is the measure of goodness of fit for the probit models of dropping out. While the largest increase in the dropping out model comes from information in the closing days of the semester, regardless of the method of R2 used, the lack of interpretability of the Maxed Rescaled R2 from SAS is less than ideal.

The focus of this study was on identifying a small number of variables to predict academic success and dropping out. This study does not suggest strategies for mitigating negative outcomes, though future research should seek to identify effective and efficient strategies for both.

Adding a Late Semester Warning Systems

Many universities have an early warning system (often midterm grade reports). While a midterm grade system may adequately capture predictions about individual course performance, this may not be the case for identifying students most at-risk for dropping out. The models suggest adding a second warning system in the closing days of the semester to identify specific classroom behaviors that may be most associated with dropping out.

The models suggest an end-of-semester warning system would have nearly the same predictive power of a model of dropping out that includes final course grades. Often final course grades are posted after students leave campus, making impossible personal, face-to-face intervention that may boost retention.

Conclusion

Given the increasing pressures on higher education to increase retention, this study contributes to the literature by examining the association between course performance and future retention and a small number of variables on a faculty would easily observe on classroom behavior and performance throughout the semester. Much of the previous work on retention focuses on factors unobservable to the faculty teaching a course or includes information at the end of the semester, when faculty often will no longer have easy opportunities to interact with students.

The models suggest that poor performance on low-impact, high frequency weekly assignments in the very close days of the semester is a key variable in helping to identify retention risks. Models of retention that include information using the closing days of the semester work nearly as well as models of retention using the final course grade. It is often much easier for a faculty member or administrators to reach a student in the closing days of a semester, rather than after final course grades are posted. This is especially true for the spring semester, where many students leave the campus for the summer.

Models of course performance have the largest gain in predictive power after the first high-impact exam. This is the appropriate window for an early warning system for course performance. However, given the models of retention show the largest gains in predictive power in the closing days of the semester, a second warning system, targeted at retention and focused on performance on low-impact, high frequency assignments in addition to overall course grades would be appropriate.

The sample in this study only considers sophomore-level principles of microeconomics course at a private Midwest university. Future extensions of this work could consider if the same pattern present itself in different years in college, in other business courses, in other academic settings, and if the effects differ in major and non-major students in a course.

A goal of this paper was to identify a small number of variables that predict performance. Given the increase in digital information available in many learning management systems, future research should investigate other key factors that predict success or retention. I would argue criteria for future models should be on keeping the set of variables small and tractable for ease of faculty integration.

End Notes

1 While exams and assignments do represent a large amount of course grade, it is less than the R2 for the model. This suggests these variables contain additional information on student individual heterogeneity relevant to course performance.

2 The full model also an adjusted R2 of 0.815. Given the small nature of the models and the sample sizes, the difference between the R2 and adjusted R2 is not large. While both are presented in the tables, the author prefers to reference R2 for regression only for the convenience of interpretation.

References

  1. Angulo-Ruiz, L.F. & Pergelova, A. (2013). The student retention puzzle revisited: The role of institutional image. Journal of Nonprofit & Public Sector Marketing, 25(4), 334-353.
  2. Astin, A.W. (1993). What matters in college? Four critical years revisited. Jossey-Bass higher and adult education series. Jossey-Bass Inc., 350 Sansome Street, San Francisco, CA 94104.
  3. Bain, C., Downen, T., Morgan, J., & Ott, W. (2013). Active learning in an introduction to business course. Journal of the Academy of Business Education, 17(1), 37.
  4. Bennett, R., & Kane, S. (2010). Factors associated with high first year undergraduate retention rates in business departments with non-traditional student intakes. The International Journal of Management Education, 8(2), 53-66.
  5. Blake, R., & Mangiameli, P. (2012). Analyzing retention from participation in co-curricular activities. Proceedings of the Northeast Decision Sciences Institute (NEDS), 21-23.
  6. Braunstein, A.W., Lesser, M.H. & Pescatrice, D.R. (2005). The business of student retention in the post September 11 environment-financial, institutional and external influences. In Allied Academies International Conference. Academy of Educational Leadership. Proceedings of the Jordan Whitney Enterprises.
  7. Cox, P.L., Schmitt, E.D., Bobrowski, P.E. & Graham, G. (2005). Enhancing the first-year experience for business students: Student retention and academic success. Journal of Behavioral and Applied Management, 7(1), 40-68.
  8. Gerdes, H., & Mallinckrodt, B. (1994). Emotional, social, and academic adjustment of college students: A longitudinal study of retention. Journal of Counseling & Development, 72(3), 281-288.
  9. hoover, e. (2016). completion grants: one part of the Student Success Puzzle. Chronicle of Higher Education, 62(25), A19.
  10. Kim, J., & Feldman, L. (2011). Managing academic advising services quality: Understanding and meeting needs and expectations of different student segments. Marketing Management Journal, 21(1), 222-238.
  11. Langbein, L.I., & Snider, K. (1999). The impact of teaching on retention: Some quantitative evidence. Social Science Quarterly, 457-472.
  12. Longden, B. (2006). An institutional response to changing student expectations and their impact on retention rates. Journal of Higher Education Policy and Management, 28(2), 173-187.
  13. Luthans, B.C., Luthans, K.W., & Jensen, S.M. (2012). The impact of business school students’ psychological capital on academic performance. Journal of Education for Business, 87(5), 253-259.
  14. Mangum, W.M., Baugher, D., Winch, J.K., & Varanelli, A. (2005). Longitudinal study of student dropout from a business school. Journal of Education for Business, 80(4), 218-221.
  15. McChlery, S., & Wilkie, J. (2009). Pastoral support to undergraduates in higher education. International Journal of Management, 8, 1.
  16. Morganson, V.J., Major, D.A., Streets, V.N., Litano, M.L. & Myers, D.P. (2015). Using embeddedness theory to understand and promote persistence in STEM majors. The Career Development Quarterly, 63(4), 348-362.
  17. O'Keeffe, P. (2013). A sense of belonging: Improving student retention. College Student Journal, 47(4), 605-613.
  18. Pearson, M. (2012). Building bridges: Higher degree student retention and counselling support. Journal of Higher Education Policy and Management, 34(2), 187-199.
  19. Rudd, D.P., Budziszewski, D.E., & Litzinger, P. (2014). Recruiting for retention: Hospitality programs. ASBBS E-Journal, 10(1), 113.
  20. Sauer, P.L., & O'Donnell, J.B. (2006). The impact of new major offerings on student retention. Journal of Marketing for Higher Education, 16(2), 135-155.
  21. Schertzer, C.B., & Schertzer, S.M.B. (2004). Student satisfaction and retention: A conceptual model. Journal of Marketing for Higher Education, 14(1), 79-91.
  22. Thompson, L.R. & Prieto, L.C. (2013). Improving retention among college students: Investigating the utilization of virtualized advising. Academy of Educational Leadership Journal, 17(4), 13-26.
  23. Tinto, V. (1987). Leaving college: Rethinking the causes and cures of student attrition. University of Chicago Press, 5801 S. Ellis Avenue, Chicago.
  24. Tompson, H., & Brownlee, A. (2013). The first year experience for business students: A model for design and implementation to improve student retention. Journal of the Academy of Business Education, 14.
  25. Wetzel, J.N., O’Toole, D., & Peterson, S. (1999). Factors affecting student retention probabilities: A case study. Journal of Economics and Finance, 23(1), 45-55.
Get the App