Research Article: 2019 Vol: 20 Issue: 4
Pupil Learning with Digital Tablet in Classroom
Anyck Dauphin, Université du Québec en Outaouais
Abstract
More and more schools are integrating digital tablets as an educational tool into the classroom. Although perceived by students and teachers as something positive, very few studies have evaluated their impacts on academic results. This gap is important given the significant cost of providing each student with a tablet. We study the case of a high school where the iPad was adopted as a classroom tool by some of its grade seven groups. We estimate the iPad's impact on grades by using a fixed-effect approach. Our results show that it has resulted in a general decline in educational achievement.
Keywords
ICT; Digital Tablets, Ipad, Pupil, Student, Education, Class, Classroom, High School, Learning Outcomes, Educational Achievement
Introduction
Educational institutions are increasingly likely to use new information and communication technologies (ICT) in their classrooms in the hope of fostering the motivation and academic achievement of their students. In high schools, this digital shift often takes the form of digital tablets. In the United States, for example, there are more than 4.5 million students using a digital tablet in the classroom on a daily basis (Etherington, 2013). The education literature is full of articles extolling the virtues of digital tablets. Some are even saying that iPads will ‘revolutionize education’ Ferenstein, (2011); Karsenti & Fievez (2013) inventoried over three hundred papers and identified sixteen assumed benefits of using digital tablets. At the head of the list of potential benefits put forward is the positive role they could have on learning and student performance. This improvement in learning and performance would arise from the possibility that the digital tablet increases motivation, simplifies access, editing and sharing of information, promotes communication and collaboration between students on the one hand, and between students and teachers on the other hand, facilitates the assessment of students by teachers and enriches the experience of reading. Some researchers also envision the following advantages: further diversification of teaching strategies, individualization of student learning, facilitation of learning to write and improvement of the organization of work. Some researchers also raise the possibility that the benefits of iPad in class might be particularly pronounced among students with learning difficulties Cumming et al., (2014); Miller et al., (2013); Watts et al., (2012). Digital tablets are also seen as a possible response to the shortage of teachers and lack of access to learning resources in remote areas in some developing countries Nedungadi, et al., (2013); Viriyapong & Harfield (2013).
The overall satisfaction of students and teachers in schools that have integrated digital tablet seems indeed quite positive as shown, for example, in literature review of Haßler et al. (2016), but few researchers have evaluated quantitatively its impact on academic outcomes, and those who have tackled this task have important methodological limitations. While many studies have been conducted on the impact of the use of computers on school outcomes, digital tablets are different from computers. Digital tablets are more portable, more intuitive and specifically designed to accommodate a number of apps that provide unprecedented opportunities for children to learn at their own pace in a stimulating environment Kucirkova (2014); Martin & Ertzberger (2013); Nguyen et al. (2015); Sung & Mayer (2013) and among the digital tablets, iPads are considered the most useful because they provide the most advanced technology and allow to use a larger number of educational apps (Karsenti & Fievez, 2013). Tablets in classrooms also have shortcomings however. One of the main issues appears to be the distraction created by non-educational uses enabled by the digital tablet, such as social networking and games Karsenti & Fievez (2013); Kinash et al., (2012); Robinson (2012); Rossing et al. (2012); Sheppard (2011); Wakefield & Smith (2012).
It seems particularly important to assess whether the advantages outweigh the disadvantages in terms of learning in view of the considerable costs incurred by the integration of such a tool (Bulman & Fairlie, 2016). The practice is indeed to provide each student with a digital tablet (1:1). The costs of the investment are therefore of the order of a few hundred dollars per student and thus of several thousand dollars at the class level. These expenses could be used for to buy other inputs that could be more efficient.
This research contributes to filling this gap as well as other shortcomings identified by the recent literature review of Pérez-Sanagustín et al. (2017). It provides evidence on the impact of digital tablets on science and mathematics achievements, among other subjects, something missing in the literature, involves more than 100 participants and is based on data collected over a whole school year. Specifically, our research question is: What is the impact of using a digital tablet in the classroom, on regular basis, in a 1:1 ratio as compared to traditional teaching, defined as teaching not relying on computers or other mobile technologies in a 1:1 ratio, in a group not limited to special needs students in a developed country. To provide an answer to this question, we examine the results of a quasi-experiment in which a Canadian high school gradually introduced the iPad into its classrooms through successive cohorts of first year students. In the first year of the project, approximately half of the seventh-grade classes were converted into iPad groups, where each child had its own iPad, paid for by the parent at the beginning of the school year, and where teachers were invited to integrate the iPad into their lessons. The following year, the school added two more iPad groups to that cohort. The students of that cohort that did not have iPads in the first year of the introduction of the iPad constitute a natural control group. We look at the impact the iPad had on the academic performance of the students in each discipline for the first year of the integration. We estimate the average impact using a fixed-effect approach with two points in time prior to high school and three points in time during the seventh grade. Our design also exploits within-teacher variation.
The next section presents the state of knowledge on the impacts of the use of digital tablets in schools. The third and fourth sections describe how the iPad was integrated in the school studied, and the data available. The next section discusses, in detail, the methodological approach we followed in estimating the iPad's impact on school performance. The estimated impacts are then reported and followed by a discussion on the limits of our research.
Literature on the Impact of Digital Tablets on Academic Performance
Since the introduction of digital tablets to the classroom, there has been a few studies that directly measure their impact on academic achievement at elementary and high schools (see the review of Nguyen et al. (2015) that is, by analysing changes in academic achievement rather than perceptions of changes in student success. In a recent literature review, highly cited by the education literature, Haßler et al. (2016) retains fourteen quantitative studies for which the “trustworthiness” of the results were high or medium (nine qualitative studies were also reviewed for a total of twenty-three studies). Among them, eight are said to provide evidence that digital tables improve learning outcomes Fernández-López, et al. (2013); Furió González et al. (2013); Lin et al., (2012); Liu (2013); Liu, et al. (2012); Riconscente (2013); Ward et al., (2013) five report no difference in learning outcomes Carr (2012); Dundar & Akcayir (2012); Huang et al., (2012); Iserbyt et al., (2014); Nedungadi et al., (2013) and one finds a negative impact on learning outcomes (Sheppard, 2011).
Two main ingredients are needed to be able to identify the causal impact of digital tablets in the classroom in an experimental setting. First, one needs a treatment group and a comparison group that are as similar as possible. More precisely, they should be statistically identical in the absence of the program and therefore expected to react to the intervention in same way. The random assignment of participants between the two groups is the gold standard to make the two groups identical. When randomized control trials are not feasible, difference-in-differences and matching methods can be used. Second, the only difference between the two groups must be the intervention. The experimental group must thus use digital tablets in the classroom, but not the comparison group. The comparison group must use the status quo method of teaching, which we consider to be teaching not relying on computers or other mobile technologies in a 1:1 ratio. It is only if these two conditions are satisfied that we can hope to identify the causal impact of the intervention.
Among the fourteen studies reviewed by Haßler et al. (2016), only four of them use a methodology that allows the identification of the impact of using the iPad on learning, that is Carr (2012); Dundar & Akcayir (2012); Iserbyt et al. (2014), who found no impact, and Sheppard (2011), who found a negative impact. None of the studies reporting positive results meets these two conditions (see the summary table of these eight studies in the appendix). Of the four studies allowing the identification of the impact of using iPad, two used samples of fewer than fifty participants: Dundar & Akcayir (2012); Sheppard (2011). We are thus left with only two studies. Carr (2012) used a quasi-experimental approach to examine the effects of iPad use as a 1:1 computing device on students' mathematics achievement with a non-equivalent group with a difference-in-differences method over one academic quarter of nine weeks. Its sample consisted of 104 fifth-grade students from two rural Virginia elementary schools. Iserbyt et al. (2014) used a randomized controlled trial to study the impact of using a tablet PC on learning basic life support and cardiopulmonary resuscitation with a sample of 128 students from a secondary school in Belgium. It is thus fair to say that rigorous evidence on the impact of the integration of iPads in the classroom is rather weak.
Although digital tablets are different from computers, we review a number of rigorous studies on the impacts of using ICT in the classroom on educational outcomes that come from the economic literature. First, Angrist & Lavy (2002) assessed the effects of a policy of computerization of primary and secondary education systems in Israel. The policy in question was designed to integrate ICT into a range of activities within schools through the financing of computers, software and teachers' training. The study found that the increased use of computers in the classroom did not lead to improved results in standardized tests. They even found that the effects were negative in math for students in the 4th grade. Leuven, Lindahl, Oosterbeek, and Webbink (2004) studied the effects of a similar program in the Netherlands targeted at primary schools with large proportions of disadvantaged students. Their results showed that access to computers had a negative impact on student learning, especially among girls.
On a more positive note, Machin et al., (2006) instead found that this type of program in the UK has helped to significantly increase the academic performance of elementary students in English and science, but not in math. Rouse et al., (2004) analysed instead, the impacts of a specific computer use, that of using Fast ForWord software for pupils with learning difficulties in reading and designed to improve their skills in language and reading. They note that the use of this software can actually advance some language skills but that it does not translate, in general, into wider language acquisition or actual reading skills. Barrow et al. (2009) also analysed the impact of a very practical use of the computer. They were interested in the software I Can Learn for the acquisition of knowledge associated with algebra. The study shows that the use of this software in the classroom actually improves student performance in algebra.
A few studies have evaluated the impact of more intensive use of computers where each student has their own laptop, as in the case studied here. One of them concerns one of the first large-scale initiatives to provide each student with a laptop in the US, which took place in the state of Maine in 2002. In that case, a computer was provided to each student and teacher in grades 7 and 8. By comparing the performance of students in writing before and after the introduction of the laptops, it was found that they had improved by about a third of a standard deviation (Maine Education Policy Research Institute, 2007). It is important to note, however, that this study included no control group, which may have skewed the results. Grimes & Warschauer (2008); Suhr et al., (2010) also examined the performance of students in California attending schools with laptops integrated into the classroom on a 1:1 basis. From a comparison between the performances of these students with students that did not attend a school with laptops, they found that the impact was negative during the first year of the program for students from 6th to 8th grades. During the second year of integration, however, the impacts became positive and managed to compensate for the initial drop. Hull & Duch (2018) also studied the impact of laptop use in a 1: 1 ratio in a mid-sized school in North Carolina. They find that while the short-term impacts of the program were nil, the mathematics scores improved by 0.13 standard deviations in the medium term.
This brief review of the literature, although incomplete, show that the impact of ICTs on school results is mixed and that a 1:1 environment seems to emerge as more promising (OECD, 2015). The lack of uniformity in the results also strongly suggest that the impact of these technologies may be inseparable from the specific uses made of them Comi et al., (2017); Falck et al., (2018) the intensity of such uses and the skills of teachers in using them.
Case Study
We studied a Quebec high school, which integrated the use of iPads in its classrooms in the 2012-2013 school year. The goal was to make the iPad a key teaching tool that students would use every day to read, to consult their textbooks and dictionaries, to take notes, to do exercises, to communicate, etc. The project was deployed gradually through successive cohorts of students entering high school.
During the year preceding the integration of the iPad into classrooms, the school informed the parents seeking a high school for their grade 6 child that it was considering the possibility of creating some classes with iPads for next year’s 7th grade. After the registration period, the school sent an email to the parents of the 209 children enrolled for grade 7 asking them if they would like their child to be in an iPad group should the project move forward. Nearly 100 parents expressed an interest. Following this very positive reception, the school decided to create three iPad groups totalling 92 students. As the number of students exceeded the number of places available, the school's administration selected the 92 students whose parents had replied earliest. Parents were asked to provide an iPad to their child before the beginning of the school year. Children whose parents had not shown interest in iPads were gathered into four regular groups that would receive a more traditional education, chalk and talk.
At the end of the 7th grade, students in regular groups were offered the opportunity to join an iPad group for the next year. The school then received enough positive responses to create two new iPad groups for grade 8. However, the parents of sixty students wanted their children to continue receiving a traditional education, so the school had to keep two regular groups. Therefore, for the second year of the ‘iPad project’, there were 5 iPad groups and 2 regular groups at the grade 8 level. That same year, and all subsequent years, all students entering the 7th grade were iPad groups.
The assignment of teachers to iPad groups was done on a voluntary basis. The school had no difficulty in finding volunteers for each of the subjects taught. An iPad was provided to each teacher the winter preceding the beginning of iPad classes. IPad teachers also received in-house training and internal technology support throughout the school year. For each subject taught, except for French and ethics, at least one teacher taught both to at least one regular group and to at least one iPad group. During the year, the iPad was used as a teaching tool where students found all their textbooks, exercise books and dictionaries. The students used it for creation, reference and consultation. Finally, iPad students were graded using the same exams and assignments as non-iPad students.
Data
In May of the first year of the iPad project, all the 7th grade students were invited to participate in the study. Every student and their parents received a consent form. Of the 206 students registered at school at that time, we received consent for 149 of them. The following year, again in May, new consent forms were submitted to students who did not consent the first year. We then obtained the consent of 9 additional students, which allowed us to observe 158 students involved in the first year of the iPad project, with 81 of them in a regular group and 77 in an iPad group. Thus, we find ourselves with a 77% participation rate for students in grade 7 in the 2012-2013 school year.
The regular students’ groups were less interested in participating with a participation rate of 71% compared to 84% for students in iPad groups. The lower participation of regular students is probably due mainly to the fact that they did not fully understand the usefulness of their participation despite the explanation given. It should also be stressed that students who did not consent to participate may be less motivated or less organized. Students were required to bring home a consent form, have it signed by their parents and then return it to school. As it is likely that students and parents who chose not to participate are different, our findings may underestimate or overestimate the average impacts of the iPad for all students. By comparing the average marks of the students who participated in the study to the weighted average marks of the groups (which includes all students), we have been able to determine that students who did not participate were, on average, slightly weaker (less than one-point difference) in French and math.
There were many departures at the end of the first year; 49 in total, including 22 who had provided consent. The cohort we observe is, thus, quite reduced in the second year. We observe only 136 students who went through the first two years of the iPad's integration. It is likely that students who left after the first year were different from those who remained, which could bias the estimates of the impact for the second year.
The student scores come from three sources: the grade 5 report card sent by parents to the high school at time of the admission request, the results of the high school admission exam, which is written in November during the 6th grade and the high school report card. These were all taken from the academic record kept by the high school for each of its students. This also includes any diagnoses that a child may have received such as ADHD, learning disabilities or mental health issues such as generalized anxiety, as well any related school intervention plan that may exist.
The grade 5 report card for the majority of the students provides numerical scores for the second and third semesters only. It is the practice of many primary schools to provide only written qualitative statements about the progress of the student for the first semester. For the majority of students, we do not have access to their 6th grade report card since only the grade 5 report card is available at time of admission. The high school admission exam includes four distinct tests: one on logic, one on math, one on French and one on personality. The scores of the four tests are available as well as the overall score for the exam for most students. It is not available for a small number of the children who registered at the school at a later time.
In addition to educational scores, data on the motivation and the profile of students were obtained through a questionnaire. Information on the perceptions and the type of use made of iPads was also collected from students and teachers who were involved in iPad groups. In total, three questionnaires were used: one for students in iPad groups, one for students in regular groups and one for teachers who work with students in iPad groups.
The questionnaire for the iPad students comprised 152 questions, of which 136 were multiple-choice questions and 16 were short answer questions. The questions were grouped into six major themes: utility of the iPad in school, uses of the iPad in class, competency with an iPad, general competency, personal information and motivation at school. The questionnaire for students in regular groups was very similar, but shorter, since some questions did not apply.
The school was responsible for distributing and recovering consent forms and questionnaires. Questionnaires for students in the classroom were filled out during a study period reserved for this activity in the month of May. Teachers were asked to return the questionnaire to the school once it was completed.
Estimation Method
Our research question is whether teaching with iPads, as an integral part of the pedagogy, in a 1:1 ratio, has a positive impact on educational outcomes in the diverse subjects taught at the high school. Rather than examining the perception of the participants by asking students and teachers if they believe that the use of the iPad in class fostered academic success, we look at their marks directly. We study only the first cohort of the iPad project because only that cohort provides a control group: students in regular groups. Without a control group, it is impossible to isolate the effect of using the iPad in the classroom from the effect of other events that have occurred during the school year. Furthermore, since many students left the school to attend another school after the 7th grade and that among those who stayed, many moved from a regular group to an iPad group, there was too few students in each type of group to properly estimate the impact the iPad had during the second year of its integration. For this reason and because the many departures could create a significant bias, we unfortunately do not consider the impact the iPad had during its second year of integration.
By ‘impact on educational outcomes’ we mean the difference between the results the iPad students had and the results they would have obtained if they had been in a regular group instead. The main methodological challenge of course is that we do not know what results the iPad students would have had if they had been in a regular group instead. One possibility would be to use the results achieved by students in regular groups, but to be allowed to do this, the students in regular groups must be ‘academically comparable’ to the students in iPad groups. Only then will the average of the students in regular groups properly represent the average that the students in iPad groups would have obtained if they had instead received a traditional education. Since assignment of students between iPad and regular groups was not random, they might not be comparable.
To judge their comparability, we would need data on multiple individual factors causing learning outcomes. These data are only available for a small subset of factors. In our case, we only observe the students' gender, the presence of a diagnosis that could hamper learning, indices of socio-economic background and of low income in the primary school area, and the admission test scores. These variables are presented in Table 1. The Figure shows that iPad groups and regular students are relatively similar with respect to the socioeconomic variables. They are aged twelve years old on average, around 45% are girls, nearly one in four students has a diagnosis that may interfere with learning, they both come from very favourable socio-economic environments, with low prevalence of low income. However, there are slight deviations suggesting that students in iPad groups are more likely to do well in school. This is consistent with the differences in the scores they obtained on the admission test which took place in the fall of grade 6: 68.7% for iPad students versus 65% for regular students in logic, 75.92% versus 71.40% in French and 76.08% versus 69.35% in math. The differences between the two groups of students are significant for French and mathematics.
| Table 1 Descriptive Statistics by Treatment Status | |||
| Variables | iPad groups | Regular groups | Difference |
| Age | 12.5 | 12.5 | -0.04 |
| -0.05 | |||
| Girls (%) | 43.8 | 45.7 | -0.02 |
| Special needs students (%) | 23.3 | 24.7 | -0.01 |
| Index socio-economic environment of the primary school area | 6.5 | 7.2 | -0.72 |
| -1.29 | |||
| Index low income in the primary school area | 9.4 | 11.2 | -1.79 |
| -0.82 | |||
| Scores 6th grade admissions exam | |||
| Academic skills | 68.8 | 65 | 3.38 |
| -2.44 | |||
| French | 75.9 | 71.4 | 4.52*** |
| -1.45 | |||
| Mathematics | 76.1 | 69.4 | 6.73*** |
| -1.74 | |||
| Personality | 73.7 | 69.9 | 4.76* |
| -2.1 | |||
| Average scores for the 5th grade | |||
| French | 78.5 | 76.2 | 2.35* |
| -1.31 | |||
| Math | 79.7 | 74.5 | 5.12*** |
| -1.57 | |||
| English | 82.2 | 78.9 | 3.38* |
| -1.95 | |||
| Science | 82.1 | 79.2 | 2.83* |
| -1.52 | |||
| History and geography | 82.2 | 78.2 | 4.05** |
| -1.62 | |||
| Ethics | 81.9 | 80.6 | 1.33 |
| -1.39 | |||
| Arts | 81.3 | 80.8 | 1.12 |
| -1.21 | |||
| Physical education (Phys ed) | 84.6 | 82.7 | 1.98 |
| -2.07 | |||
| N | 77 | 81 | |
The grades both types of students have obtained at the end of their primary schooling are presented at the bottom of Table 1. It shows the average results for the 5th grade for iPad and regular students in each of the subjects taught at primary school. In French, students from iPad groups were getting on average 78.52%, while those from regular groups were getting 76.17%. In math, the average for the students in iPad groups amounted to 79.65% while it stood at 74.53% for students in regular groups. In English, the average was 82.24% versus 78.86%, 82.051% versus 79.23% in science, and so on. The differences are statistically significant at the 5% level for math and history & geography and at the 10% level for French, English and science. Students from iPad groups were thus indeed stronger than the students from regular groups at the end of their primary school education, at least in the main subjects.
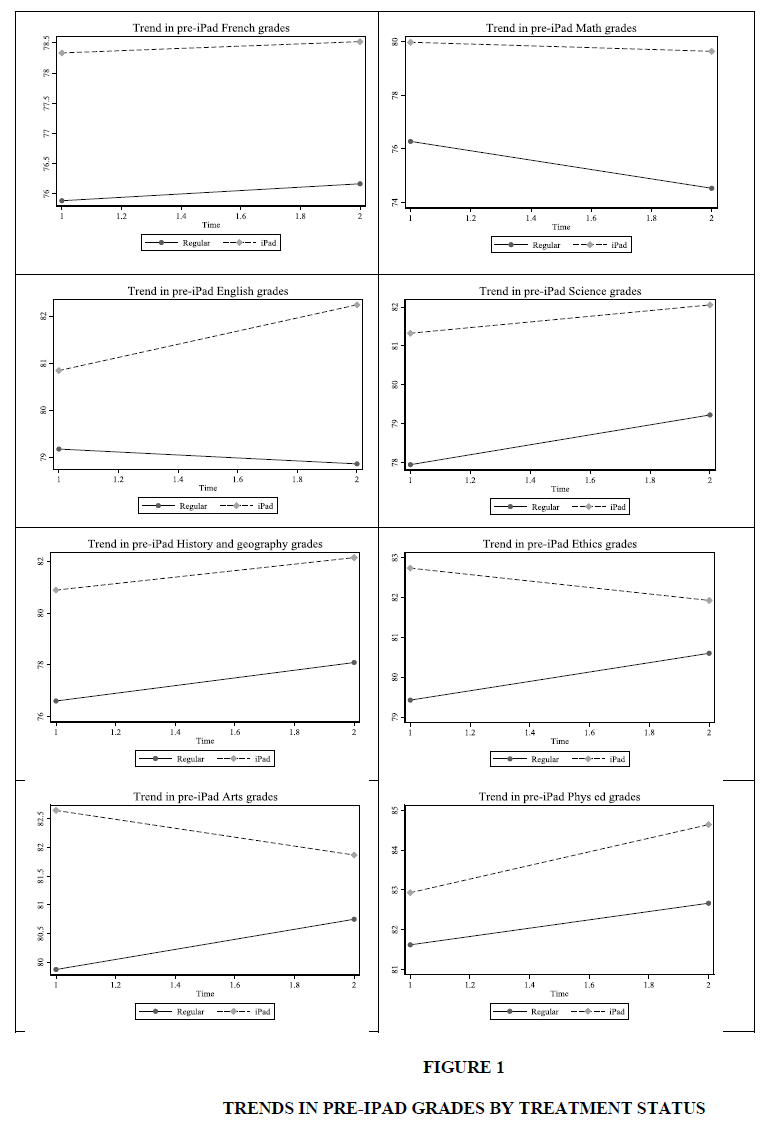
Since, obviously, the two types of students are not comparable academically, we cannot assume that the results achieved by the regular students in the 7th grade are a good indication of the results that the iPad students would have obtained had they been in a regular group. What we can do instead, is to assume that the evolution of the marks of the students from the two groups would have been the same. That is to say, in the absence of iPads, the average grades of iPad and regular students would have evolved in the same way during the first year of high school, so that the gap between the two would have remain constant. The students in iPad groups would thus have remained stronger than students in regular groups. To verify the likelihood of this hypothesis, we examined the evolution of the grades of the two types of students during the fifth year, from the second to the third trimester. Figure 1 plots the average of each group for each term. The differences between the averages of the two types of students are relatively stable in French, mathematics, science, history and geography, and physical education. In English, the gap is increasing, while in ethics and arts it is decreasing.
Since we only have two pre-treatment periods, we also performed a parallel trend hypothesis test by estimating the following model:
![]()
where denotes the student and t the time period, Y is the student’s score, T2 is a binary variable equal to 1 when t= 2 and 0 otherwise, P is a binary variable taking the value 1 if the student is in the treatment group and 0 otherwise, n captures the combined effect on Y of all the student’s variables that are constant over time, and u is the idiosyncratic error term. The null hypothesis that the trend of the two groups is identical is β3 = 0. Since we observe two periods per student and we expect those observations to be correlated, the error terms are clearly clustered at the level of the student. In the presence of clustered error terms, OLS estimates are not biased, but standard errors can be highly underestimated, leading to incorrect inference, and particularly to falsely high t-statistics. For this reason, we used a cluster-robust standard error estimator. The results of the OLS estimation are presented in Table 2. As we can see, the assumption that the two trends are parallel is rejected at 10% for English, but is not rejected for the other topics.
| Table 2 OLS Estimates with Student Fixed-Effect of a Different Trend | ||||
| Subject | Constant | β3 | N | R2 |
| French | 77.04 (0.22) |
-0.25 (0.90) |
308 | 0.004 |
| Math | 78.11 (0.30) |
1.40 (1.23) |
312 | 0.027 |
| English | 80.80 (0.32) |
3.39* (1.76) |
245 | 0.077 |
| Science | 78.84 (0.68) |
1.12 (2.28) |
244 | 0.042 |
| History and geography | 78.82 (0.56) |
1.58 (2.46) |
239 | 0.017 |
| Ethics | 80.72 (0.46) |
-1.62 (1.78) |
261 | 0.016 |
| Arts | 81.10 (0.30) |
-2.04 (1.26) |
289 | 0.021 |
| Phys ed | 82.80 (0.21) |
0.73 (1.64) |
211 | 0.014 |
If one is ready to make this hypothesis, then we can measure the impact of the iPad by comparing the evolution of the marks of iPad students to the evolution of the marks of regular students. Comparing changes in the marks, rather than comparing the marks themselves, not only eliminates the effect of ‘academic’ differences between the two types of students, but also eliminates the effect that other events, experienced by both of them, could have had on the evolution of academic performance, such as adaptation to high school. An ideal approach to control for the fact that the two groups of students are different would have been to use the students that integrated iPad groups the second year of the project as the control group. Unfortunately, we observe only 57 of them. This limits greatly the size of the group of regular students sharing the same teacher as the students in iPad groups.
Another aspect to consider when estimating the impact of the iPad on academic performance is the role of teachers. It is well known that teachers have differentiated impacts on the academic performances of their students. They may have different teaching styles and different assessment practices. To be able to isolate the effect of the iPad from the effect of the teacher, we need to compare the evolution of students in iPad groups to the evolution of students in regular groups who have had the same teacher in grade 7. As mentioned earlier, for each subject taught, except for French and ethics, at least one teacher taught both at least one regular group and at least one an iPad group, which allows us to adequately estimate the impact of the iPad for these subjects.
In more technical terms, we are using a fixed-effect approach with two points in time prior to high school and three points in time during the seventh grade and where the teacher is controlled for except for French and ethics. For each subject, the regression equation is thus:
![]()
where τ is an intercept that is different for each period, T345 is a binary variable equal to 1 when t = 3,4,5 and 0 otherwise, X is set of dummies controlling for the teacher in high school, δ is the student fixed effect, and ε is the idiosyncratic error term. The coefficient α2 provides the effect of using a tablet in the classroom. Furthermore, since we observe five periods per student and we expect those observations to be correlated, we used again a cluster-robust standard error estimator.
Results and Discussion
The Table 3 shows our estimates of the impact by subject. As explained, these are based on a within-student and within-teacher variation comparison of students from iPad and regular groups that had the same teacher for that subject, except for French and ethics since it was not possible. For these subjects, our estimates are based on students who have not had the same teacher during their 7th grade, and therefore, do not isolate the iPad effect from the teacher effect. We ran the same regressions using the group of students that integrated iPad groups the second year of the project as the control group instead and the estimates obtained are qualitatively the same as those presented in Table 3. Therefore, the results for French and ethics are presented for indicative purposes only. The results for English are also provided for information only, as the time trend prior to high school is not parallel. For these three subjects, the results are presented in italics.
| Table 3 OLS Estimates With Student and Time Fixed-Effects of the Impact of the Ipad on Educational Outcomes | ||||
| Constant | α2 | N | R2 | |
| French | 77.13*** (0.38) |
-6.32** (1.03) |
782 | 0.356 |
| Math | 78.10*** (0.54) |
-1.25 (2.60) |
786 | 0.198 |
| English | 80.12*** (0.52) |
-1.72 (1.36) |
719 | 0.093 |
| Science | 79.16*** (0.81) |
-2.69** (1.36) |
718 | 0.116 |
| History and geography | 78.91*** (0.79) |
-3.18* (1.62) |
710 | 0.077 |
| Ethics | 81.05*** (0.71) |
-2.39 (1.61) |
735 | 0.132 |
| Arts | 81.27*** (0.50) |
-0.83 (1.44) |
763 | 0.272 |
| Phys ed | 82.29*** (0.38) |
-0.82 (1.03) |
684 | 0.113 |
In math, the average impact of the iPad on student achievement throughout the year is estimated at -1.25 point. In science and history & geography, the impacts are also negative but stronger. We estimated that the students from iPad groups would have obtained, on average, higher ratings of 2.69 points in science if they had been in a regular group instead. In history & geography, the marks would have been higher by 3.18 points. However, the estimated impacts are statistically significant only in science, at 5%, and in history & geography, at 10%. In math, the variance of the impact is very high.
Various factors may explain why the iPad's impact varied from one discipline to another. Some disciplines are probably more amenable to the use of the iPad, some teachers are probably more comfortable with ICT, the use of the iPad may have been more frequent in some disciplines, the types of uses of the iPad may have varied from one discipline to another, etc. Comi et al., (2017); Falck, et al., (2018) show that the impacts of using laptops in the classroom vary according to the use made. The data collected on questionnaires from iPad students and teachers provide us with information on the frequency of use of the iPad by discipline. Table 4 presents the compilation of the students’ and teachers’ responses. In French, 80% of students believe that the iPad was used in almost all classes while 20% believe it was used every two classes. In math, 63% believed that the iPad was used in almost all courses, while 35% thought that it was used every two classes. Although students do not all agree on the iPad's usage frequency in the different disciplines, it seems pretty clear that it is in French and math that it was the most used. It also seems to have been commonly used in English and history & geography. Phys ed and arts classes are the two disciplines which least used the iPad. Given the very low use of the iPad in the gym and arts classes, it is logical that we found that the iPad had not had a significant impact on the results in these two disciplines.
| Table 4 Use of the Ipad by Discipline | ||||||
| According to the students | Almost every class | Every two classes | One class in three | One class in four | Seldom | Never |
| French | 80% | 20% | ||||
| Math | 63% | 35% | 2% | |||
| English | 50% | 39% | 9% | 2% | ||
| Sciencea | NA | NA | NA | NA | NA | NA |
| History & geography | 34% | 29% | 23% | 5% | 8% | 2% |
| Ethics | 16% | 41% | 20% | 17% | 6% | |
| Arts | 11% | 14% | 15% | 55% | 5% | |
| Phys ed | 97% | 3 % | ||||
| According to the teachers | Frequency of use with students | Number of mandatory school tasks per week | Number of non-mandatory school tasks per week | |||
| French | 2-3 times per week | 5 to 6 | 0 | |||
| English | 2-3 times per week | 1 to 2 | 1 to 2 | |||
| Science | Once a week | 1 to 2 | 0 | |||
| History | Every day | 1 to 4 | 1 to 2 | |||
| Arts | Once a week | 0 to 2 | 1 to 2 | |||
| Phys ed | Once per term | 0 | 1 to 2 | |||
Teachers’ questionnaires also provide information about the frequency with which they used the iPad, but we lack the information for three disciplines: math, geography and ethics. The data in Table 4 confirms that the iPad has been used more frequently in French, English and history than in arts and gym classes. Its strong use in history might explain the greater impact observed for that subject.
As already mentioned, the students forming the iPad and regular groups are different. We chose the methodological approach best suited to address these differences given the data available. Our methodological approach allows us to eliminate the effect of all the features distinguishing the iPad and regular students that were constant from grade 5 to grade 7, such as the gender of the students, their (innate) intellectual abilities, a diagnosis that could hamper learning, their birth date, etc. Our approach also allows us to partial out the effect that the teacher may have had on educational outcomes except in French and ethics. For the other subjects, estimates are derived from a comparison of students that had the same teacher in grade 7th.
Another potential source of error comes from the fact that the participation rate is not 100%. It is possible that students who did not want to participate in our study are different from those who agreed to participate and this could have biased our estimates. Finally, our sample is small.
The objective of this study was to assess the relevance of investing in digital tablets in high school by evaluating the impact that the use of the iPad in the classroom had on educational outcomes. We studied the case of a Canadian high school which introduced the iPad in some of its 7th grade groups in 2012-2013. We estimated the iPad's impact on grades by discipline for the first year of the integration. The estimation strategy was to compare the performance of students in ‘iPad groups’ to that of students in ‘regular groups’ using a fixed-effect approach with two points in time prior to the integration of the iPad and three points in time after and where the teacher was controlled for except for French and Ethics. Where possible, our estimates are thus derived from a comparison of students that had the same teacher in grade 7 in order to control for the effect that the teacher may have had on educational outcomes.
Our results indicate that the introduction of the iPad has not led to a general increase in academic performance. Instead, in science and history & geography, the average impact of the introduction of the iPad on grades is estimated respectively at -2.69 and -3.18 points, both significant at 5% and 10%. This means that students in iPad groups would have had, on average, a score of 2.69 and to 3.18 points higher in science and in history & geography. For math, the estimates are not significant from zero. These differentiated impacts between subjects suggest that the impacts of the iPad depend on the type of integration and the kind of uses made of it, something that should be explored in the future to enhance the positive effects of the iPad.
Based on the results for the first year of introduction of the iPad, the investment does not seem profitable. It is true that we cannot exclude the possibility that the negative effects partially faded or even reversed in the second and subsequent years, as teachers acquired a mastery of this new pedagogical tool and came to exploit its educational potential, as found by Grimes and Warschauer (2008); Suhr et al., (2010) who studied the integration of laptops into the classroom on a 1:1 basis. However, given the paucity of empirical evidence on the impact of digital tablets in schools and the mixed evidence for the impact of computers access on educational outcome, it is surprising to see the enthusiasm and eagerness of the educational community to make such a costly and risky digital shift.
References
- Angrist, J., & Lavy, V. (2002). New Evidence on Classroom Computers and Pupil Learning. Economic Journal, (112), 735-765.
- Barrow, L., Markman, L., & Rouse, C. (2009). Technology’s Edge: Educational Benefits of Computer-Aided Instruction. American Economic Journal: Economic Policy, (1), 52–74.
- Bulman, G., & Fairlie, R. W. (2016). Technology and education: Computers, software, and the Internet. In R. Hanushek, S. Machin and L. Woessmann (Ed.), Handbook of the Economics of Education (5), pp. 239-280. Amsterdam: North Holland.
- Carr, J.M. (2012). Does math achievement h‘APP’en when iPads and game-based learning are incorporated into fifthgrade mathematics instruction? Journal of Information Technology Education Today, 11(1), 269–286.
- Comi, S.L., Argentin, G., Gui, M., Origo, F., & Pagania, L. (2017). Is it the way they use it? Teachers, ICT and student achievement. Economics of Education Review, (56), 24-39.
- Cumming, T. M., Strnadová, I., & Singh, S. (2014). iPads as instructional tools to enhance learning opportunities for students with developmental disabilities: An action research project. Action Research, 12, 151–176.
- Dundar, H., & Akcayir, M. (2012). Tablet vs. paper: The effect on learners’ reading performance. International Electronic Journal of Elementary Education, (4), 441–450.
- Etherington, D. (2013). Apple Has Sold Over 8M iPads Direct to Education Worldwide, with more than 1B iTunes U Downloads. Retrieved from http://techcrunch.com/2013/02/28/apple-has-sold-over-8m-ipads-directto-education-worldwide-with-more-than-1b-itunes-u-downloads/
- Falck, O., Mang, C., & Woessmann, L. (2018). Virtually No Effect? Different Uses of Classroom Computers and their Effect on Student Achievement. Oxford Bulletin of Economics and Statistics, 80(1), 1-38.
- Ferenstein, G. (2011). How the iPad2 Will Revolutionize Education. Retrieved from http://www.fastcompany.com/1733662/how-ipad-2-will-revolutionize-education
- Fernández-López, Á., Rodríguez-Fórtiz, M. J., Rodríguez-Almendros, M. L., & Martínez-Segura, M. J. (2013). Mobile learning technology based on iOS devices to support students with special education needs. Computers & Education, 61, 77–90.
- Furió, D., González-Gancedo, S., Juan, M., Seguí, I., & Costa, M. (2013). The effects of the size and weight of a mobile device on an educational game. Computers & Education, (64), 24–41.
- Grimes, D., & Warschauer, M. (2008). Learning With Laptops: A Multi-Method Case Study. Journal of Computing Research, 38(3), 305-332.
- Haßler, B., Major, L., & Hennessy, S. (2016). Tablet use in schools: a critical review of the evidence for learning outcomes. Journal of Computer Assisted Learning, (32), 139-156.
- Huang, Y.M., Liang, T.H., Su, Y.N., & Chen, N.S. (2012). Empowering personalized learning with an interactive e-book learning system for elementary school students. Educational Technology Research and Development, (60), 703–722.
- Iserbyt, P., Charlier, N., & Mols, L. (2014). Learning basic life support (BLS) with tablet PCs in reciprocal learning at school: Are videos superior to pictures? A randomized controlled trial. Resuscitation, 85(809–813).
- Karsenti, T., & Fievez, A. (2013). The iPad in education: uses, benefits, and challenges - A survey of 6,057 students and 302 teachers in Quebec, Canada. Retrieved from CRIFPE, Montréal, QC.:
- Kinash, S., Brand, J., & Mathew, T. (2012). Challenging mobile learning discourse through research: student perceptions of Blackboard Mobile Learn and iPads. Australasian Journal of Educational Technology, 28(4), 639–655.
- Kucirkova, N. (2014). iPads in Early Education: Separating Assumptions and Evidence. Frontiers in Psychology, 5, 1-3.
- Leuven, E., Lindahl, M., Oosterbeek, H., & Webbink, D. (2004). The Effect of Extra Funding for Disadvantaged Pupils on Achievement. The Review of Economics and Statistics, 89, 721–736.
- Lin, C.-P., Wong, L.-., & Shao, Y.-. (2012). Comparison of 1:1 and 1:m CSCL environment for collaborative concept mapping. Journal of Computer Assisted Learning, 28, 99–113.
- Liu, T.C., Lin, Y.C., & Paas, F. (2013). Effects of cues and real objects on learning in amobile device supported environment. British Journal of Educational Technology, 44, 386–399.
- Liu, T.C., Lin, Y.C., & Paas, F. (2014). Effects of prior knowledge on learning from different compositions of representations in a mobile learning environment. Computers & Education, 72, 328–338.
- Liu, T.C., Lin, Y.C., Tsai, M.J., & Paas, F. (2012). Splitattention and redundancy effects on mobile learning in physical environments. Computers & Education, 58(1), 172–180.
- Machin, S., Mcnally, S., & Silva, O. (2006). New Technology in Schools: Is There a Payoff? Economic Journal, 117, 1145–1167.
- Maine Education Policy Research Institute. (2007). Maine’s Middle School Laptop Program: Creating Better Writers.
- Martin, F., & Ertzberger, J. (2013). Here and now mobile learning: An experimental study on the use of mobile technology. Here and now mobile learning: An experimental study on the use of mobile technology, 68, 76–85.
- Miller, B.T., Krockover, G.H., & Doughty, T. (2013). Using iPads to teach inquiry science to students with a moderate to severe intellectual disability: A pilot study. Journal of Research in Science Teaching, 50, 887–911.
- Nedungadi, P., Raman, R., & McGregor, M. (2013). Enhanced STEM learning with online labs: Empirical study comparing physical labs, tablets and desktops. Paper presented at the Frontiers in Education Conference.
- Nguyen, L., Barton, S.M., & Nguyen, L.T. (2015). iPads in higher education—Hype and hope. British Journal of Educational Technology, 46(1), 190-203.
- Pérez-Sanagustín, M., Nussbaum, M., Hilliger, I., Alario-Hoyos, C., Heller, R.S., Twining, P., & Tsai, C.C. (2017). Research on ICT in K-12 schools - A review of experimental and survey-based studies in computers & education 2011 to 2015. Computers & Education, 104, 1-15.
- Riconscente, M.M. (2013). Results from a controlled study of the iPad fractions gameMotion Math. Games and Culture, 8, 186–214.
- Robinson, R. (2012). Experiential learning in a newmillennium: the implications of iPad technology in instructional settings. Paper presented at the Society for Information Technology & Teacher Education International Conference.
- Rossing, J.P., Miller, W.M., Cecil, A K., & Stamper, S.E. (2012). iLearning: the future of higher education? Student perceptions on learning with mobile tablets. Journal of the Scholarship of Teaching and Learning, 12(2), 1–26.
- Rouse, C., Krueger, A., & Markman, L. (2004). Putting Computerised Instruction to the Test: A Randomized Evaluation of a ‘Scientifically-Based’ Reading Program. Economics of Education Review, 23, 323-338.
- Sheppard, D. (2011). Reading with iPads – The difference makes a difference. Education Today, 11, 12–15.
- Suhr, K., Hernandez, D., Grimes, D., & Warschauer, M. (2010). Laptops and Fourth-Grade Literacy: Assisting the Jump over the Fourth-Grade Slump. The Journal of Technology, Learning, and Assessment, 9(5), 1-45.
- Sung, E., & Mayer, R.E. (2013). Online multimedia learning with mobile devices and desktop computers: An experimental test of Clark’s methods-not-media hypothesis. Computers in Human Behavior, 29, 639-647.
- Viriyapong, R., & Harfield, A. (2013). Facing the challenges of the One-Tablet-Per-Child policy in Thai primary school education. International Journal of Advanced Computer Science & Applications, 4, 176–184.
- Wakefield, J., & Smith, D. (2012). From Socrates to satellites: iPad learning in an undergraduate course. Creative Education, 3(5), 643–648.
- Ward, N.D., Finley, R.J., Keil, R.G., & Clay, T.G. (2013). Benefits and Limitations of iPads in the High School Science Classroom and a Trophic Cascade Lesson Plan. Journal of geoscience education, 61, 378–384.
- Watts, L., Brennan, S., & Phelps, R. (2012). iPadiCan: Trialling iPads to support primary and secondary students with disabilities. Australian Educational Computing, 27, 4-12.
Appendix
| Appendix 1 Summary Table of the Studies Reporting Positive Learning Outcomes According to Haßler et al. (2016) | |||||
| Studies | Objectives | Method | Sample | Outcomes Variables | Results |
| Fernández-López et al. (2013) | To design and test the impact of a mobile platform on iPad and iPod touch devices that covers the main phases of the learning process and tailored to special needs students. | Pre/post design after 6 months of use in the classroom without a control group. | 34 students with special education needs from Spain. | Basic learning skills in language, math, environmental awareness, autonomy and social | Increased skills in the five areas considered. |
| Furio et al. (2013) | To test whether an iPhone game has better learning outcomes than a traditional game on a tablet PC. | Rotation design between iPhone and tablet without a control group not relying on computers or a mobile device during a summer school in Spain. | 79 children ranging from 8 to 10 years old from Spain. | Knowledge about the water cycle | Very high scores for the two devices, and a statistically significant difference in favour of the iPhone. |
| Lin et al. (2012) | To compare the impact of a collaborative concept mapping for social sciences in a 1:1 and a 1:m environment. | Pre/post design with a group operating in a 1:1 ratio and another in a 1:m ratio, with random assignment between them. No control group not relying on computers or a mobile device. | 64 children 11-12 years old from a primary school in Taiwan. | Learning, knowledge retention, quality of artefacts, interactive patterns | Improved learning and retention in both settings. Superior group participation, communication and interaction for the 1:m setting, superior artefacts for the 1:1 setting. |
| Liu et al. (2012) | To investigate split-attention and redundancy effects in a mobile learning environment as a function of different combinations of media. | Pre/post design with three conditions: texts with pictures embedded in the mobile device (TP); texts embedded in the mobile device and real objects (TO); and texts with pictures embedded in the mobile device and real objects (TPO). No control group not relying on computers or a mobile device. | 81 children with a mean age of 11 from three classes of a public elementary school in northern Taiwan. | Comprehension and learning efficiency about the plant leaf | No difference between the TP condition and the TO condition in comprehension and learning efficiency, but both conditions performed better than the TPO condition. |
| Appendix 2 Summary Table of the Studies Reporting Positive Learning Outcomes According to Haßler et al. (2016) | |||||
| Studies | Objectives | Method | Sample | Outcomes variables | Results |
| Liu et al. (2013) | To investigate whether arrow‐line cues can improve the effectiveness and efficiency of learning in a mobile device supported learning environment with or without the use of real objects. | Pre/post design with four conditions: cued text with pictures (CTP), un-cued text with pictures (UTP), CTP and objects, and UTP and objects, with a random assignment between the four conditions. All conditions used an iPad-like tablet. | 74 students with a mean age of 11 from a primary school in Taiwan. | Knowledge about the plant leaf | Higher efficiency of the cued conditions than the un‐cued conditions. No difference between the cued conditions with or without real plants. |
| Liu et al. (2014) | To examine the effects of prior knowledge on learning from different compositions of representations in a mobile learning environment. | Prior knowledge of the students was first tested. According to their score, they were divided into low and high prior knowledge groups. Students from the two groups were randomly assigned to two conditions: text and photo vs. text, photo, and real object. No control group not relying on computers or a mobile device. | 78 fifth-grade students of a primary school in Taiwan. | Knowledge about the plant leaf | Students who learned with tablet PCs only outperformed students who additionally learned with real plants on a comprehension and an application test. |
| Riconscente (2013) | To investigate whether the iPad fractions game Motion Math would improve fractions knowledge and attitudes. | Rotation design where students in the treatment condition played Motion Math daily for 20 min over five consecutive school days and the control group had regular mathematics instruction that did not target fractions. Students randomly assigned between the two groups. | 122 fifth graders enrolled in two schools in southern California. | Fractions knowledge | Students’ fractions test scores improved significantly with an average of over 15%. |
| Ward et al (2013) | To explore the utility of a set of tablet-based personal computers in the K–12 science, technology, engineering, and mathematics classroom. | Pre/post design without a control group. A lesson on food-chain dynamics and predator–prey population controls was designed on the Applet iPad platform and delivered to three ecology classes. | 49 students from grades 9-12 from a Washington state high school. | Knowledge on food-chain dynamics and predator–prey population controls | Students who showed a strong initial understanding retained the same level of understanding, while students who had the lowest initial understanding showed the most improvement in understanding. |