Research Article: 2018 Vol: 19 Issue: 3
The Impact of Simulation Activity on Student Performance
Steven D. Dolvin, Butler University
Mark K. Pyles, College of Charleston
Abstract
Keywords
Simulations, Investments, Finance, Portfolio Return.
Introduction
Traditional classroom instruction (i.e., lecturing) is generally considered to be highly effective in terms of transferring knowledge and, as such, has steadfastly remained the dominant method in higher education, particularly for those areas that are considered more quantitative. For example, studies have shown that the “chalk and talk” method of instruction is still most popular in finance courses (Saunders, 2001; Farooqi & Saunders, 2004; Iqbal et al., 2006), as well as courses in related disciplines such as economics (Becker & Watts, 1996; Becker & Watts, 2001).
An argument could be made that one of the primary objectives of higher education is preparation for a professional career upon graduation. There is naturally more to this preparation than knowledge attainment. The application of this knowledge to “real world” situations is a skill that has historically been largely left to the students’ own devices, and often insufficiently. However, in recent years, there has been much discussion on the use of classroom games and simulations as a way to fill this gap.
The use of games in instruction is far from a new concept, as there is evidence as early as the 1940s (Chamberlin, 1948) of their use in Economics courses. However, Holt (1999) shows there has been much more emphasis over recent decades, due in large part to the rapid rise in technology, which allows easier integration into the classroom. In addition, part of the reasoning behind the low levels of use was there was little research documenting a benefit in student learning from classroom simulations; however, recent works, including Cebula & Toma (2002), Dicle & Levendis (2011), Chen & Jaiprakash (2017) and Druckman and Ebner (2018), have addressed this latter issue, finding a positive influence from “bringing course material to life”. More generally, Harter & Harter (2010) and Day (2015) find that stock market simulations can significantly increase financial literacy among high school students, and Moffit et al. (2010) find that students completing an equity trading game believe their knowledge levels have improved, as has their interest in the topic.
While there has been ample research documenting the potentially positive benefits of integrating trading simulations into investments classes, to our knowledge none of these existing studies investigate whether increased simulation activity has a more profound impact. As such, we examine whether students who are more active in trading simulations generally earn higher course grades as a result. We find that this is indeed the case, as increased trading activity has a significantly positive influence on overall course grade.
Given this result, we also explore whether instructors can induce increased activity level and produce the same outcome. In particular, we segment classes and add a minimum trading requirement. In contrast to our expectation, we find that this requirement does not induce incremental trading activity. In fact, the average number of trades actually falls, suggesting that such a requirement leads students to treat the simulation as more of an assignment than as an overall experience. Moreover, we do not find any significant influence, on average, on the student grades as a result of “forced” activity. So, we generally see no overall benefit from adding such a requirement.
In ancillary results, we find that increased trading activity is also associated with higher simulation returns. This finding is in contrast to existing literature, but it is likely a function of the educational environment. In particular, some students likely make a handful of trades (potentially enough to meet assignment requirements or simply to explore trading), then they simply stop or lose interest, allowing their portfolios to suffer as a result. Thus, the inherent differences between simulations (i.e., “fake” money) and real life (i.e., “real” money) are likely the driving element behind this finding.
Literature Review
The literature relevant to the history of games in the business classroom is large and developed, particularly with respect to economics courses. Chamberlin (1948) is credited with the first application of games in a classroom setting. Specifically, Chamberlin (1948), using doctoral students at Harvard, allowed the students to circle the room and negotiate trades with others. Some individuals were designated buyers, while some were sellers; the interaction of the two groups led to further understanding of how markets work. Others, including Smith (1962), quickly built upon this, and the use of games in economics courses became relatively widespread. Davis & Holt (1993) and Kagel & Roth (1995) survey the work done on the topic to that point. Brauer & Delemester (2001) extend the survey by completing a more comprehensive review of the existing games for Economics courses at that time.
Fels (1993) brings to light the fact that, although not unusual, the use of games prior to the mid-1990s never became common-place. The two reasons suggested by Fels (1993) were high costs of creation and relatively low documentation of significant student benefit in terms of increased knowledge attainment. The first issue has been largely overcome due to the rapid rise in technology and related computer-based simulations available at reasonable costs. The implementation of easy-to-use simulations such as the Stock Market Game (SMG) or Stock-track has led to the more evolved and involved electronic simulations available today. Also, the ease of use of such programs makes the opportunity cost for the instructor minimal, Wood et al. (1992) and Bell (1993) for early examinations of the SMG.
The second issue is more involved, but it too has been largely resolved, with the dominant conclusion that classroom games do provide benefit for the students. Frank (1997) found that students who experienced a classroom environment using games performed better on multiple choice tests than did counterparts in classrooms without games. Dickie (2006) finds evidence that also supports this contention. Gremmen & Potters (1997) find that students that experienced games learned more about the economic model than those who did not. Mullin & Sohan (1999) and Yandell (2004) find no significant difference in test results dependent upon the use of games; however, they find that students generally are more satisfied with the course if there is a game involved.
Fraas (1980) finds that the students’ pre-course level of knowledge was a significant contributing factor in the effectiveness of the games. Students that had little prior knowledge received more benefit from the games than those students with higher starting knowledge levels. Tsigaris (2008) suggests there is a double dividend from experimental games. The instructor, assuming they are utility maximizers, should perhaps incorporate games in order to increase their course evaluations. In addition, the students may benefit from increased knowledge that the real-world application of material provides. Tsigaris (2008) also states that the intensity of the simulation is an important element in the effectiveness of the classroom game. Cebula & Toma (2002) find empirical support for both of these notions.
While evidence on experimental games in economics courses is abundant, the same is not true in finance. Unfortunately, until recently the use of such games in finance courses has been much less examined, due in part to the slow acclimation of the discipline to computer-based simulations. In fact, Clinebell & Clinebell (1995) show finance courses were often slow to use computers in their instruction despite being available, yet Devasagayam & Hyat (2007) find evidence that supports the use of computer simulations as a pedagogical device in a cross-disciplinary study of finance and marketing courses. Foster et al. (2006) and Helliar et al. (2000) find more specific evidence that a market-share game can improve student learning in undergraduate finance courses.
Some examples of past literature in the area are only peripherally related to the finance classroom. For example, Breen & Boyd (1976) present an early programming guide for creating simulations that would be applicable in money and banking classes. Also, Bell’s (1993) version of the non-computerized SMG was primarily designed for investment analysis, as stated by the author. There is also very little evidence on the effectiveness of these experimental games in helping students clarify their opinions on disciplines as a whole, perhaps as a viable career option. An exception is Sherman et al. (2008), who find that the use of experimental methods generally increase the impact of the course on a student’s choice of becoming an entrepreneur.
There are a few notable exceptions that are similar in nature to the current study. King & Jennings (2004) find that the inclusion of trading simulation increases student learning. Ascioglu & Kugle (2005) implement a surveying technique to examine the influence of simulations on student enjoyment and learning objectives. Levkin (2005) examines whether there is a relationship between trading ability (i.e. performance) and academic performance (i.e., grade) and largely finds success in either is independent of the other. Huang & Hsu (2011) find that the use of online games (including a stock market simulation) helps achieve significantly higher learning outcomes, but caution they should be used as a learning supplement rather than as a primary vehicle of instruction. Wu et al. (2012) uses a virtual stock trading system to examine whether such a system can help students make rational investments and promote active learning and finds support for these notions.
Finally, Dolvin & Pyles (2011) expand on these results, finding that the experience of taking an investments course with an integrated trading simulation has a positive influence on student interest, knowledge, and experience; however, in contrast, they find no consistent relation between simulation returns, market returns, or market volatility and changes in either interest level, likelihood of future management of money, or knowledge levels. Thus, Dolvin & Pyles (2011) conclude that the prevalence of benefits documented in prior literature, combined with the lack of negative side effects from poor student performance on such simulations, suggests that the use of such investment simulations is warranted.
While the literature is generally conclusive with regard to the positive benefits of integrating trading simulations into investment courses, it is surprising that there appears to be no existing literature addressing whether increased activity in such simulations can incrementally add to the benefits. Thus, we attempt to fill this apparent gap.
Method
For the simulation, each student has a fictitious trading account (through Stock-Trak) seeded with $1 million. In effect, the students are treated as investors who have just opened trading accounts and are free to invest in any security they choose (i.e., equity, derivatives, fixed income, etc.). The only instructions would be for those sections with a minimum trading requirement, indicating the types of trades (e.g., equity, bonds, and options) and orders (e.g., market, limit, and stop) they need to complete. Further, students are never graded based upon their trading performance (rather just the completion of activities and submitted reports thereon). Students can also not see any of their classmates’ activities, other than overall class rankings.
We have collected data from multiple sections of investments courses across time, capturing a total of 478 useable student observations. Each student observation includes basic characteristics, such as major and gender. In addition, we also record the overall course grade each student received, as well as his/her overall activity and performance in the investment simulation. Lastly, we also capture course specific information, e.g., term, class time, class size, and whether a minimum trade requirement was employed. Unfortunately, due to IRB (Institutional Review Board) restrictions, we are unable to capture some student-specific information, such as pre-existing GPA. While this limits some of our analysis, we believe that we can still draw meaningful conclusion from our results. We report our summary results in Table 1.
| Table 1 Summary Statistics |
|||||||
| Total | Segment by Active | Segment by 25Min | |||||
| High | Low | p-value | Yes | No | p-value | ||
| N | 478 | 244 | 234 | 419 | 59 | ||
| Grade | 82.17 | 84.30 | 79.95 | 0.00 | 82.33 | 81.02 | 0.38 |
| Ret | 2.54 | 3.76 | 1.29 | 0.24 | 3.22 | -2.16 | 0.10 |
| ExRet | -1.14 | 0.55 | -2.91 | 0.10 | -0.87 | -3.07 | 0.50 |
| Summer | 0.10 | 0.19 | 0.00 | 0.00 | 0.05 | 0.46 | 0.00 |
| Male | 0.73 | 0.77 | 0.69 | 0.05 | 0.73 | 0.75 | 0.80 |
| Fin Major | 0.71 | 0.70 | 0.72 | 0.61 | 0.71 | 0.71 | 0.93 |
| Trades | 29.95 | 47.43 | 11.72 | 0.00 | 29.07 | 36.17 | 0.08 |
| TradesPerWk | 2.34 | 3.85 | 0.77 | 0.00 | 2.11 | 3.96 | 0.00 |
| Active | 0.51 | 1.00 | 0.00 | na | 0.47 | 0.78 | 0.00 |
| 25Min | 0.86 | 0.81 | 0.94 | 0.00 | 1.00 | 0.00 | na |
| Class Size | 30.07 | 28.92 | 31.27 | 0.00 | 30.99 | 23.54 | 0.00 |
| 8 am | 0.46 | 0.38 | 0.54 | 0.00 | 0.52 | 0.00 | 0.00 |
| Note: Grade is the percentage score received by the student for the overall class. Ret is the return on the simulated Stock-track account over the investment period. ExRet is the excess return on the simulated Stock-track account over the investment period, calculated as Ret minus the return on the S&P 500 over the same time period. Summer is a dummy variable equal to 1 if the course was a summer course, zero otherwise. Male is a dummy variable equal to one if the student was male, zero otherwise. Fin Major is a dummy variable equal to 1 if the student is financing major, zero otherwise. Trades are the total number of trades made by a student over the entire course. TradesPerWk is the total trades made by the student divided by the number of weeks in the course. Active is a dummy variable equal to 1 if the student made more than the median number of trades per week. 25Min is a dummy variable equal to 1 if the respective course included a requirement that students make at least 25 trades during the semester. Class Size is the total number of students in the course. 8 am is a dummy variable equal to 1 if the class met at 8 am. p-values are calculated assuming unequal variances and test the differences between the respective columns. | |||||||
Table 1 first presents averages for the total sample. The average course grade (Grade) across all students and sections is an 82.17 percent, and the average total return (Ret) earned during the investment simulation, which for a semester is roughly a three month period, was 2.54 percent. Given that stock market conditions can be quite variable across semesters, we also calculate excess returns (ExRet), which is defined as the student’s return less the return on the S&P500 for the same time period. Adjusting for market conditions, the average student has an excess return of -1.14 percent.
Across our sample, approximately 10 percent of the observations come from summer sessions. Approximately 73 percent are male (Male), and 71 percent are finance majors (Fin Major). In a typical session, the average student makes approximately 30 total trades (Trades), which are about 2.34 trades per week (TradesPerWk) on average. To segment the students, we define students with an above median number of trades as Active. With regard to course specific items, 86 percent of the student observations were subject to a minimum trade requirement of 25 trades (25Min). The average class size (Class Size) was just over 30 students, and 46 percent of the observations occurred during an 8am session (8am).
The remainder of Table 1 segments our data using two different approaches. First, we segment by those students who were more active in the simulation (i.e., above median trade levels) versus those with lower activity. We find that more active students earn a higher grade (about 4.35 percent higher) and have a higher return, particularly excess return, which is more than 3.5 percent higher. Consistent with existing literature (Barber & Odean, 2001), we find that males are more active in their trading, but, as we discuss later, we also find that male students have lower grades. So, there may be some overlapping influence, which we will control in the upcoming regression analysis. We also find that classes with fewer students are more active. At the beginning of each class session, the simulation is used as a discussion of current events, so each student sees where she/he ranks in the class. Thus, smaller classes make it more difficult for students to “hide their results”, potentially creating an indirect incentive to be more active in the simulation. Even though class meeting time has no impact on the structure of the class or simulation, we find that students in an 8 am section are less active, so some halo effect may potentially exist and carry over to the outside simulation.
Second, we segment by students who were in sections that had a minimum trade requirement. The underlying rationale for including such a requirement is that increased simulation activity should increase learning and, therefore, grade. In contrast, however, we find that there is no difference in grade, so such a requirement does not appear to have the intended effect. In addition, we find no difference in excess returns. Most surprising, adding a minimum trade requirement has the opposite effect of our intention, as students, on average, end up being less active in the simulation. Our working theory is that setting a trade requirement causes students to treat the simulation as more of an assignment than as a deeper learning experience and real world activity. We note, however, that class sizes (not by design) are larger for those that had the 25Min requirement, so there could potentially be some indirect influence.
To explore our summary statistics in more detail, in Table 2 we also segment our observations by grade and by excess return, each segmented into High (above median) and Low (below median) categories. Beginning with the segmentation by grade, we find that students with higher grades have higher simulated investment returns though not significantly higher. As noted above, male students receive a larger portion of low grades. Surprisingly, finance majors do not earn higher grades. One possible explanation revolves around the fact that the class is a requirement for all finance majors, but students with other majors may take the course as an elective or professional qualification (i.e., actuarial science students). As such, students who are not finance majors have specifically chosen to enroll, likely due to a specific interest in the course. Combined with the fact that they must have the same prerequisites to take the course, the added interest may lead to the higher grades. As noted above, we also find that students with higher grades are more active in the simulation. Interestingly, we also find that larger classes exhibit higher average grades; however, we note that the average class size is only different by one student. So, the low variation in class size may make this difference effectively meaningless.
| Table 2 Summary Statistics Segmented By Student Performance |
||||||
| Segment by Grade | Segment by ExRet | |||||
| High | Low | p-value | High | Low | p-value | |
| N | 238 | 240 | 237 | 241 | ||
| Grade | 90.27 | 74.14 | 0.00 | 83.31 | 81.05 | 0.02 |
| Ret | 3.71 | 1.40 | 0.28 | 12.32 | -7.05 | 0.00 |
| ExRet | -0.14 | -2.13 | 0.36 | 8.50 | -10.62 | 0.00 |
| Summer | 0.08 | 0.12 | 0.24 | 0.10 | 0.10 | 0.81 |
| Male | 0.70 | 0.77 | 0.09 | 0.75 | 0.71 | 0.36 |
| FinMajor | 0.68 | 0.73 | 0.21 | 0.69 | 0.73 | 0.36 |
| Trades | 34.51 | 25.43 | 0.00 | 34.04 | 25.92 | 0.00 |
| TradesPerWk | 2.64 | 2.05 | 0.01 | 2.63 | 2.06 | 0.01 |
| Active | 0.59 | 0.43 | 0.00 | 0.56 | 0.46 | 0.04 |
| 25Min | 0.90 | 0.85 | 0.14 | 0.88 | 0.88 | 0.94 |
| ClassSize | 30.56 | 29.58 | 0.07 | 30.16 | 29.97 | 0.72 |
| 8am | 0.47 | 0.45 | 0.72 | 0.48 | 0.44 | 0.32 |
| Note: Both Grade and ExRet are segmented by their respective median values. All other variables are as previously defined. p-values are calculated assuming unequal variances and test the differences between the High and Low columns. | ||||||
Examining our segmentation by excess return, we continue to find that students with higher simulated portfolio returns also earn higher grades. So, either superior performing students earn higher returns due to innate ability, or they are simply also more active, which benefits them in this context. Otherwise, we find no meaningful differences. In unreported results, we also examine our data segmented by Top, which is a variable that identifies if a student earned a return that ranked him/her in the top half of their respective class. The intuition is that a student could earn a low return, but if it was better than their classmates, it still may reflect incremental learning. However, we find no differences relative to segmenting by return, so we continue to focus on return as opposed to ranking.
Results
Given that we have noted numerous potential overlapping relationships, we next turn to a regression framework. Thus, to more completely examine the significant impacts of our primary variables, we follow Dolvin and Pyles (2011) and consider three variations of the following basic model, which we report in Table 3.
| Table 3 Multivariate Regressions, LOGIT/OLS |
||||||
| Active | Grade | ExRet | ||||
| Coef. | P>Chi Sq. | Coef. | p-value | Coef. | p-value | |
| Intercept | 1.11 | 0.24 | 80.79 | 0.00 | -16.90 | 0.08 |
| Active | 5.15 | 0.00 | 4.27 | 0.06 | ||
| 25Min | 0.50 | 0.20 | 1.94 | 0.24 | 1.29 | 0.73 |
| Summer | -4.24 | 0.00 | -2.92 | 0.24 | 1.59 | 0.78 |
| Male | 0.41 | 0.06 | -1.43 | 0.18 | 0.38 | 0.88 |
| FinMajor | 0.13 | 0.56 | -1.85 | 0.07 | 2.82 | 0.24 |
| ClassSz | -0.04 | 0.10 | -0.00 | 0.98 | 0.32 | 0.27 |
| 8am | 0.29 | 0.17 | -0.48 | 0.64 | 0.99 | 0.68 |
| N | 478 | 478 | 478 | |||
| % Conc./Adj. R-Sq. | 64.3 | .0526 | .0006 | |||
| Note: Given that it is a binary variable, the regression of Active is based on a logistic model. The Grade and ExRet regressions are based on traditional OLS models. All variables are as previously defined. | ||||||
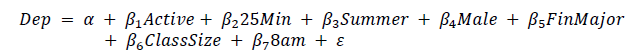
In particular, in our first specification we define Active as our dependent variable. Given that it is a binary variable, we employ a logistic regression approach. This analysis allows us to specifically examine whether a minimum trade requirement has an impact on activity level. For our second and third specifications, we define Grade and ExRet, respectively, as our dependent variables. In each of these specifications we employ a standard regression analysis. This analysis will provide additional evidence in regard to the impact of activity level on performance.
Beginning with Active, we find that students enrolled during a summer session are less active, likely as a result of a more compressed schedule. Male students continue to be more active, as expected, even after controlling for other variables. Also, students who are in sections with larger enrollments continue to be less active. Most importantly, we find that adding a minimum trade requirement does not have a significant impact on activity level. So, it seems that those students who take an interest on their own, thereby increasing simulation activity, are the most likely to benefit. Stated differently, adding a minimum requirement does not appear to be a sufficient condition to generate student interest in the simulation and, therefore, the learning that it supports.
Turning to class performance, we find that finance majors continue to have significantly lower course grades even after controlling for other factors. As we proposed earlier, we believe this is potentially due to the fact that the course is a requirement for all finance majors, as opposed to a targeted elective for other students. In contrast to our earlier results, we find that class size is not significantly related to course grade, but, again, this result (or lack thereof) could simply be due to the lack of variation in course enrollments across sections. We again find that male students have lower grades, but this result is not highly significant. Most importantly (and also most significantly) is Active, as we find that students who are more engaged in the simulation have higher grades. In particular, students with above median levels of activity earn, on average, a grade that is five percent higher than their less active peers. In unreported results, we also define activity using TradesPerWk, finding that our results are robust to this specification. In fact, we find that increasing activity by one trade per week results in an average grade increase of approximately one percent.
It is possible that there is some endogeneity impacting the relationship between activity and grades. In particular, are “better” students simply more engaged in the simulation, or does the simulation actually help create “better” students? To control for this issue, in unreported results we conduct a two-stage least squares in which we first predict student grade based on demographic data, thus attempting to control for possible endogeneity. We then use the predicted grade in the subsequent regressions. Our results of this analysis remain robust, suggesting that overall simulation activity does have a significantly positive impact on class grade. Thus, while our prior regression suggests instructors cannot force engagement via trade requirements, it nonetheless appears that more engagement in trading simulations is indeed beneficial and should therefore be encouraged.
Lastly, we examine ExRet. The only significant independent variable that we find is activity level. In particular, higher simulation activity continues to result in higher simulated portfolio returns. This finding is in contrast to the existing literature, but as we propose earlier, it is likely a function of the environment. Some students make a handful of trades (potentially enough to meet assignment requirements), then they simply stop or lose interest. Particularly when some trades may be based on derivatives, which are quite leveraged, the result on return can be devastating. Thus, we do not believe that our finding adds anything incremental to the existing literature, but is more a reflection of student interest, which adds to our earlier conclusions i.e., engagement matters. In unreported results we also explore whether overall market return during a given semester has an impact; however, we find that adding a variable to capture the return of the S&P 500 has no significant impact in any of the models nor does it affect the significance of the other variables.
Conclusion
Using data from a basic investments course over multiple semesters, we address two primary questions. First, we explore whether students who are more active in a simulated trading portfolio perform better in the investments course-both by grade and by investment return. Our results suggest that this is indeed the case, as more active participation in the investment simulation, even after controlling for other factors, results in both a higher average grade and a higher average portfolio return. Second, we explore whether instructors can influence simulation participation level by adding a basic minimum trade requirement. Unfortunately, we find that adding this requirement does not increase participation and may in fact result in lower average activity levels, as students may simply view the simulation as an assignment and do the bare minimum. In future research, it might be beneficial to explore whether a more robust, higher minimum requirement has the intended effect. If not, then it becomes more of the instructor’s responsibility to create engagement-beyond simple simulation requirements.
References
- Ascioglu, A., & Kugle, L.P. (2005). Using trading simulations to teach microstructure concepts. Journal of Financial Education, 31(2), 69-81.
- Barber, B., &. Odean, T. (2001). Boys will be boys: Gender, overconfidence, and common stock investment. Quarterly Journal of Economics, 116(1): 261-292.
- Becker, W.E., & Watts, M. (1996). Chalk and talk: A national survey on teaching undergraduate economics courses. American Economic Review, 86(2), 448-453.
- Becker, W.E., & Watts, M. (2001). Teaching methods in US undergraduate economics courses. Journal of Economic Education, 32(3), 269-279.
- Bell, C.R. (1993). A noncomputerized version of the Williams and Walker stock market experiment in a finance course. Journal of Economic Education, 24(4), 317-323.
- Brauer, J., & Delemeester, G. (2001). Games economists play: A survey of non-computerized classroom games for college economics. Journal of Economic Surveys, 15(2), 221-236.
- Breen, W., & Boyd, J. (1976). Classroom simulation as a pedagogical device in teaching money and banking. Journal of Financial and Quantitative Analysis, 11(4), 595-606.
- Cebula, R., & Toma, M. (2002). The effect of classroom games on student learning and instructor evaluations. Journal of Economics and Finance Education, 1(2).
- Chamberlin, E.H. (1948). An experimental imperfect market. Journal of Political Economy, 56(2), 95-108.
- Chen, L., & Jaiprakash, P. (2017). An insurance market simulation with both adverse and advantageous selection. Risk Management and Insurance Review, 20(1), 133-146.
- Clinebell, J.M., & Clinebell, S.K. (1995). Computer utilization in finance courses. Financial Practice and Education, 5(1), 132-42.
- Davis, D., & Holt, C. (1993). Experimental economics. Princeton University Press.
- Day, S.H. (2015). The stock market game taught me to be more careful with my money: A closer look. Journal of Consumer Education, 30, 30-44.
- Devasagayam, R., & Hyat, S. (2007). Pedagogical value of computer-based simulations: A cross disciplinary study. International Journal of Business Research, 7(5), 89-95.
- Dickie, M. (2006). Do classroom experiments increase learning in introductory microeconomics. Journal of Economic Education, 37(3), 267-288.
- Dicle, M., & Levendis, J. (2011). The DL-trading game. Journal of Financial Education, 37 (1/2), 55-82.
- Dolvin, S., & Pyles, M. (2011). The influence of simulation activity on student interest. Journal of Economics and Economic Education Research, 12(3): 35-48.
- Druckman, D., & Ebner, N. (2018). Discovery learning in management education: Design and case analysis. Journal of Management Education, 42(3): 347-354.
- Farooqi, N., & Saunders, K.T. (2004). A note on teaching methods: The Canadian experience. Advances in Financial Education, 2(1), 52-56.
- Fels, R. (1993). This is what I do, and I like it. Journal of Economic Education, 24(4), 365-370.
- Foster, F.D., Gregor, S., Heaney, R., Northcutt, W., O’Neill, T., Richardson, A., Welch, E., & Wood, R. (2006). Impact of computer based share market simulations on learning: A link between self-efficacy and understanding. Journal of College Teaching and Learning, 3(2), 45-60.
- Fraas, J. W. (1980). The use of seven simulation games in a college economics course. The Journal of Experimental Education, 48(4), 264-280.
- Frank, B. (1997). The impact of classroom experiments on the learning of economics: An empirical investigation. Economic Inquiry, 35(4), 763-769.
- Gremmen, H., & Potters, J. (1997). Assessing the efficacy of gaming in economic education. The Journal of Economic Education, 28(4), 291-303.
- Harter, C., & Harter, J.F.R. (2010). Is financial literacy improved by participating in a stock market game? Journal for Economic Educators, 10(1), 21-32.
- Helliar, C.V., Michaelson, R., Power, D. M., & Sinclair, C. D. (2000). Using a portfolio management game (Finesse) to teach finance. Accounting Education, 9(1), 37-51.
- Holt, C.A. (1999). Teaching economics with classroom experiments: A symposium. Southern Economic Journal, 65(3), 603-610.
- Huang, C.W., & Hsu, C.P. (2011). Using online games to teach personal finance concepts. American Journal of Business Education, 4(12), 33-38.
- Iqbal, A.M., Farooqi, M.N., & Saunders, K.T. (2006). Teaching methods and assessment techniques used for the introductory level undergraduate finance course in British and Irish Universities. Journal of Economics and Finance Education, 5(1), 47-61.
- Kagel, J.H., & Roth, A.E. (1995). The Handbook of Experimental Economics. Princeton University Press.
- King, D.A., & Jennings, W.W. (2004). The impact of augmenting traditional instruction with technology-based experiential exercise. Journal of Financial Education, 30(2), 9-25.
- Levkin, B.J. (2005). Some evidence regarding computer-based financial instrument trading simulations and their use as an assessment tool. Journal of Financial Education, 31(2), 23-33.
- Moffit, T., Stull, C., & McKinney, H. (2010). Learning through equity trading simulation. American Journal of Business Education, 3(2).
- Mullin, R.D., & Sohan, G.E. (1998). Benefit assessment of classroom experimental economics. USAF Academy.
- Saunders, K.T. (2001). Teaching methods and assessment techniques for the undergraduate introductory finance course: A national survey. Journal of Applied Finance, 11(1), 110-112.
- Sherman, P.S., Sebora, T., & Digman, L.A. (2008). Experimental entrepreneurship in the classroom: The effects of teaching methods on entrepreneurial career choice intentions. Journal of Entrepreneurship Education, 11, 29-42.
- Smith, V.L. (1962). An experimental study of competitive market behavior. Journal of Political Economy, 70(2), 165-179.
- Tsigaris, P. (2008). Is there a double dividend from classroom experimental games? American Journal of Business Education, 1(1), 23-35.
- Wood, W.C., O'Hare, S.L., & Andrews, R.L. (1992). The stock market game: Classroom use and strategy. The Journal of Economic Education, 23(3), 236-246.
- Wu, H.C., Tseng, C.M., Chan, P.C., Huang, S.F., Chu, W.W., & Chen, Y.F. (2012). Evaluation of stock trading performance of students using a web-based virtual stock trading system. Computers & Mathematics with Applications, 64(5), 1495-1505.
- Yandell, D. (2004). Effects of integration and classroom experiments on student learning and satisfaction. Journal of Economics and Economic Education Research, 5(3), 17-27.